【摘要】:图3.8.3 CZT变换的循环卷积图注:M≤n≤L-1时,y[n]和hL[n]的循环卷积不代表线性卷积。由式可以看出,线性系统h[n]是非因果的,当n的取值为0到N-1,k的取值为0,1,…h[n]y[n]的点数为2N+M-2,因而用循环卷积代替线性卷积且不产生混叠失真条件是循环卷积的点数应大于或等于2N+M-2。进行循环卷积的另一个序列只需要将y[n]补上零值点,使之成为L点序列即可,如图3.8.3c所示。
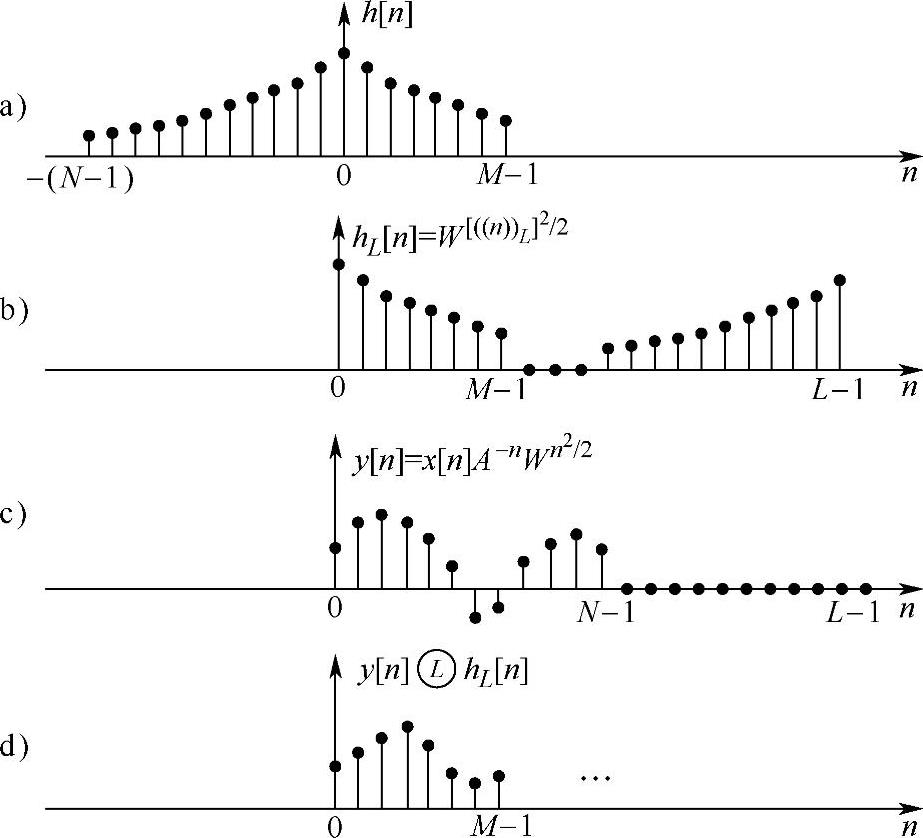
图3.8.3 CZT变换的循环卷积图
注:M≤n≤L-1时,y[n]和hL[n]的循环卷积不代表线性卷积。(https://www.xing528.com)
由式(3.8.9)可以看出,线性系统h[n]是非因果的,当n的取值为0到N-1,k的取值为0,1,…,M-1时,h[n]是在-(N-1)到M-1之间取值。也就是说,h[n]是一个有限长序列,点数为N+M-1,如图3.8.3a所示。输入信号x[n]也是有限长序列,点数为N。h[n]∗y[n]的点数为2N+M-2,因而用循环卷积代替线性卷积且不产生混叠失真条件是循环卷积的点数应大于或等于2N+M-2。但是,由于只需要前M个值X(zk)(k=0,1,…,M-1),对以后的其他值是否有混叠失真并不感兴趣,这样可将循环卷积的点数缩减到最小为N+M-1。当然,为了进行基2快速傅里叶变换运算,循环卷积的点数应取为L≥N+M-1,同时又满足L=2m的最小L。这样可将h[n]先补零值点,补到点数等于L,也就是从n=M开始补L-(N+M-1)个零值点,补到n=L-N处,或补L-(N+M-1)个任意序列值,然后将此序列以L为周期而进行周期延拓,再取主值序列,从而得到进行循环卷积的一个序列,如图3.8.3b所示。进行循环卷积的另一个序列只需要将y[n]补上零值点,使之成为L点序列即可,如图3.8.3c所示。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




