算法基本原理解析

已知有限长序列x[n]（0≤n≤N-1）的z变换为

为适应z可以沿z平面更一般的路径取值，故沿z平面上的一段螺线作等分角的采样，z的这些采样点z_k为

z_k=AW^-k （k=0，1，…，M-1） （3.8.2）

式中

即

z_k所沿的轨迹如图3.8.1所示。在式（3.8.5）及图3.8.1中，M为所要分析的复频率的点数，即采样点的总数，不一定与x[n]的长度相等；A为采样轨迹的起始点位置，由它的半径A₀及相角θ₀确定。通常A₀≤1，否则z₀将处于单位圆z=1的外部。W为螺线参数，W₀表示螺线的伸展率，W₀＞1时，随着k的增加螺线内缩，W₀＜1时，则随k的增加螺线外伸。φ₀是采样点间的角度间隔。由于φ₀是任意的，减小φ₀就可提高频率分辨率，这对分析具有任意起始频率的高分辨率窄带频谱是很有用的。当M=N，A=A₀e^jθ0=1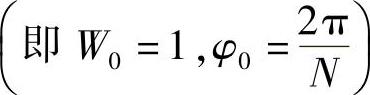，时，线性调频z变换就是离散傅里叶变换。

图3.8.1 CZT在z平面上的轴线轨迹

z变换在这些采样点的值为

(www.xing528.com)

直接计算式（3.8.6），与直接计算离散傅里叶变换相似，总共算出M个采样点，需要NM次复数乘法与（N-1）M次复数加法。当N、M很大时，这个量很大，这就限制了运算速度。但是，下面将看到，通过一定的变换，以上运算可以转换为卷积形式，从而可以采用快速傅里叶变换算法，这样就可以大大提高运算速度。在式（3.8.6）中，令

把式（3.8.7）代入式（3.8.6）得

令

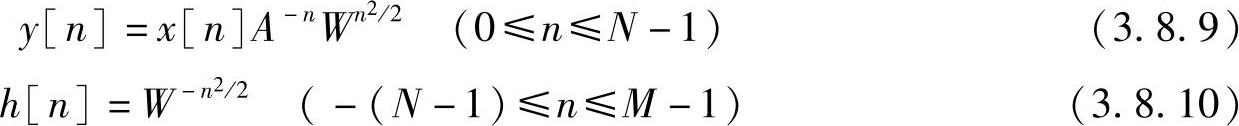
则

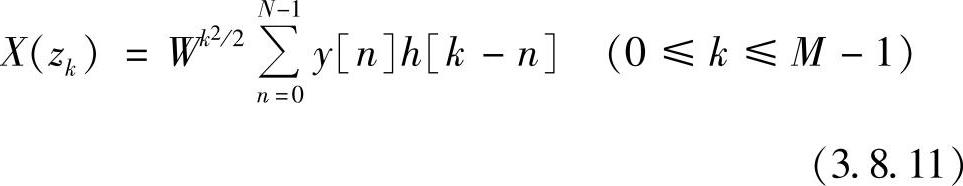
CZT算法框图如图3.8.2所示。

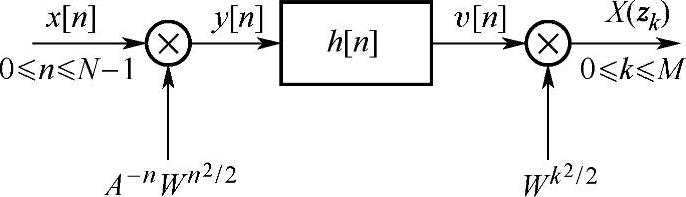
图3.8.2 CZT算法框图