分裂基快速傅里叶变换算法优化技巧

基4快速傅里叶变换算法比基2快速傅里叶变换算法复数乘法次数减少，但如果不满足N=4^m就无法用基4快速傅里叶变换进行运算。观察式（3.2.2）可以发现，x[n]中的偶序号部分快速傅里叶变换运算所需的乘法次数比奇序号部分乘法次数少，因而对于n为偶数部分利用基2快速傅里叶变换算法，而奇数部分用基4快速傅里叶变换算法，则运算量可进一步降低。1984年，法国的杜阿梅尔（P.Dohamel）和霍尔曼（H.Hollmann）把基2分解和基4分解融合在一起，提出“分裂基”快速傅里叶变换算法（Split-RadixFFT，SRFFT），这种算法在目前已知的N=2^m点快速傅里叶变换算法中乘、加次数最少，已经非常接近理论上所需乘法次数的最小值，而且它的运算结构（或流图）与基2快速傅里叶变换相似，没有更多额外的取指或存储数据的运算，特别适宜用专用集成电路实现。

分裂基算法与混合基算法不同之处在于，分裂基算法同一级内既有基2部分又有基4部分，而不像组合数快速傅里叶变换中同一级内只用同一种基运算。它们的相似之处是可以有时间抽取算法，也可以有频率抽取算法。下面以时间抽取算法来说明分裂基的算法原理。

设N=2^m，将x[n]分成三个子序列，即

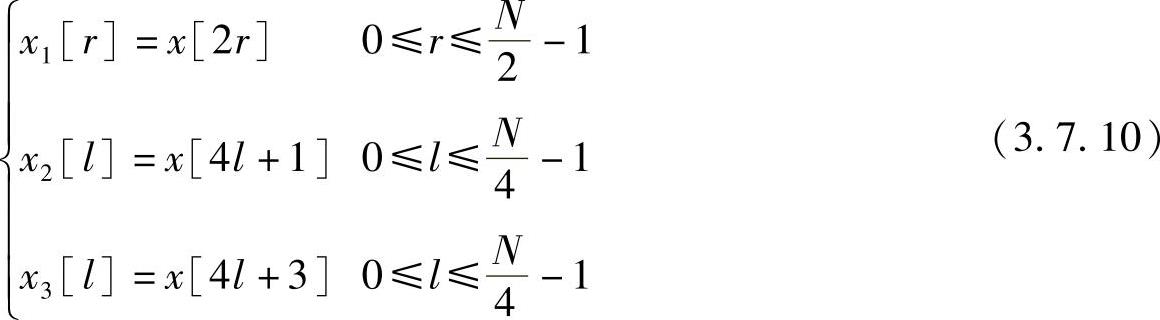
做离散傅里叶变换运算，有

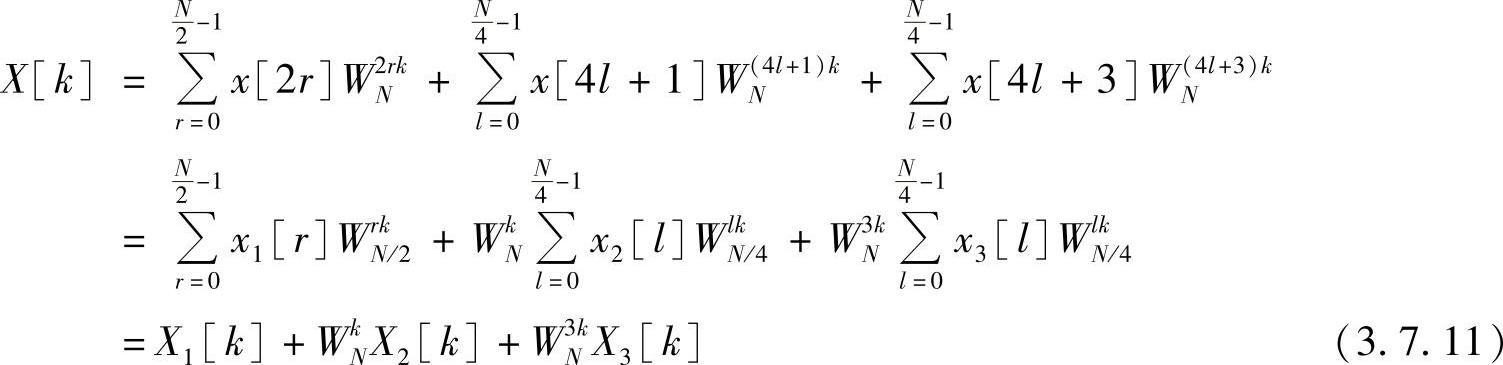
式中，X₁[k]为x₁[r]的N/2点离散傅里叶变换；X₂[k]为x₂[l]的N/4点离散傅里叶变换；X₃[k]为x₃[l]的N/4点离散傅里叶变换。因此有

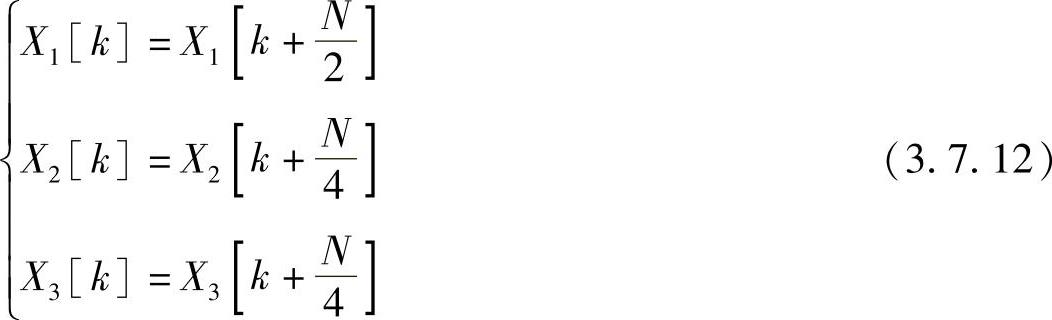
于是式（3.7.11）中X[k]可分解成下列各式，即

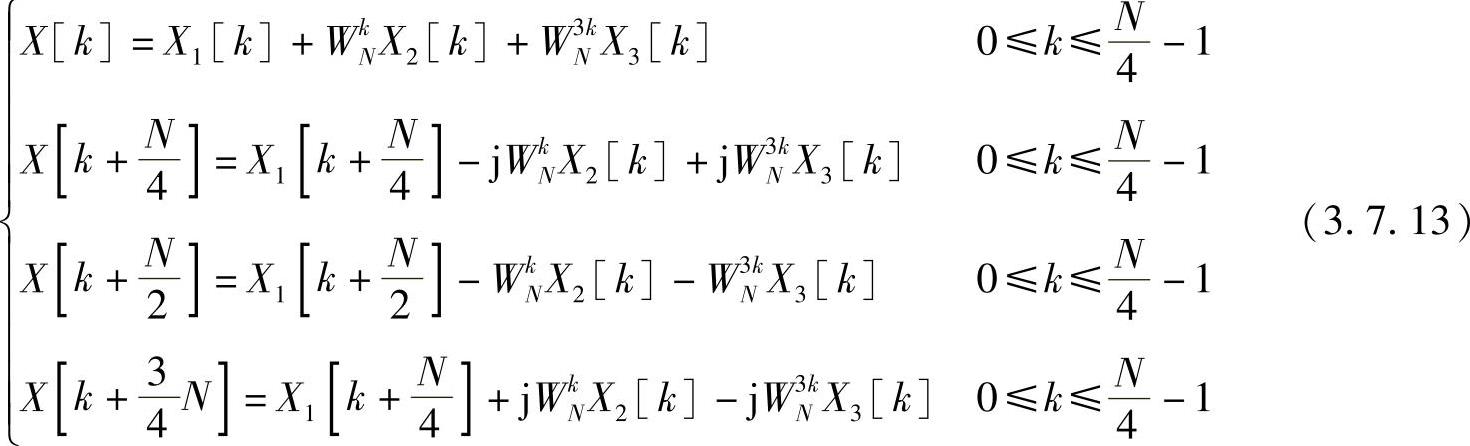
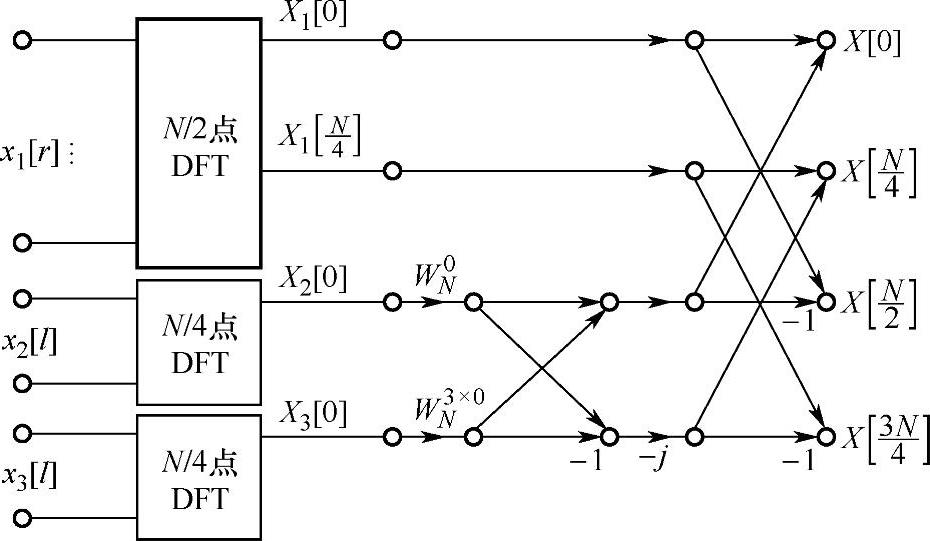
这个关系可以用图3.7.2表示。接着对N/2点离散傅里叶变换和N/4点离散傅里叶变换按以上方法分解成三部分，如此进行到最后不能再分解为止。图3.7.3是N=2⁵=32点时分裂基流图示意图。图中阴影部分表示2点离散傅里叶变换；未标阴影线、形如倒“L”部分表示分裂基运算，其中数字表示分裂基运算的蝶形个数。分裂基基本蝶形运算如图3.7.4所示，它由4个输入4个输出组成倒L形的流图，每一基本蝶形运算需要2次复数乘法和6次复数加法。

根据图3.7.2和图3.7.4可以统计出分裂基快速傅里叶变换算法的运算量。当N=2^m时，流图可分成m级，设第l级共有N_l个倒L形蝶形，第l+1级有N_l+1个倒L形蝶形，第l级的N个数据中，有4N_l属于本级蝶形，而2N_l+1个属于下一级蝶形，因此有

N=4N_l+2N_l+1

或

(www.xing528.com)

图3.7.2 分裂基DIT-FFT算法的第一级分解流图

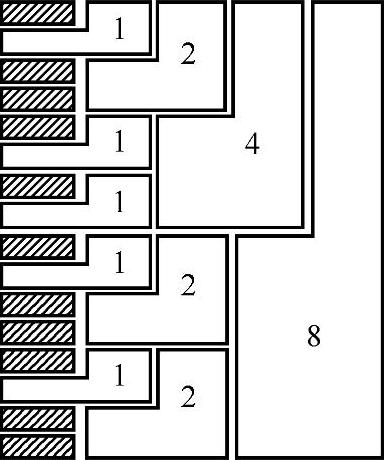
图3.7.3 N=2⁵的分裂基流图框图

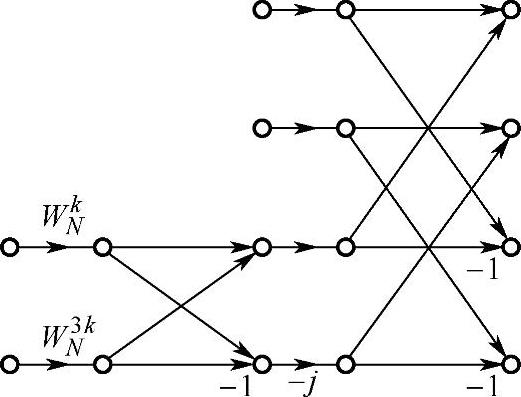
图3.7.4 分裂基DIT-FFT的基本蝶形运算

第一级（l=1）比较特殊，只有基2蝶形运算，而无倒L蝶形；第m级（l=m）有N/4个倒L蝶形。这样求解式（3.7.14）所示的差分方程，并利用l=m时的边界条件N_m=N/4，即可求得第l级倒L蝶形个数为

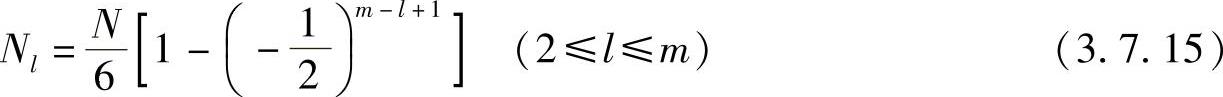
于是全部倒L形蝶形个数N_total为

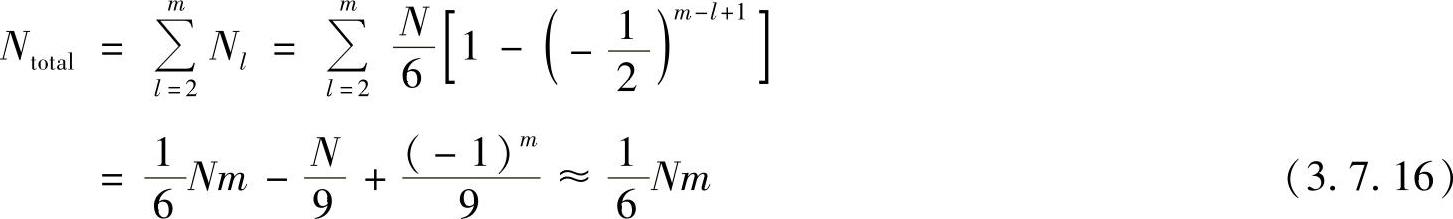
每个倒L蝶形需要2次复数乘法和6次复数加法，所以分裂基快速傅里叶变换算法的复数乘法次数m_c和复数加法次数a_c分别为

a_c=Nm=Nlog₂N （3.7.18）

式（3.7.17）的分裂基复数乘法次数与基2快速傅里叶变换复数乘法次数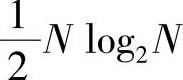相比约可节省33%乘法次数，与基4快速傅里叶变换复数乘法次数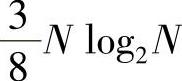相比可节省约11%乘法次数。以上比较尚未计入式（3.7.16）中的后面两项减少的运算量。分裂基快速傅里叶变换算法运算量最少，计算结构规整，且具有原位运算特点及内部数据不需要重排等优点，是目前N=2^m算法中比较理想的一种快速傅里叶变换算法。