快速傅里叶变换算法的频率抽取数学表示

时间抽取算法把n分解成二进制表示，然后一步一步计算。如果把k分解成二进制表示，则可以得到另外一类快速傅里叶变换，称为频率抽取快速傅里叶变换。

仍假设N是2的整数次幂（如果不是，可以通过对序列补零使之变成2的整数次幂），N=2^m，则任意n=0，1，…，N-1可表示为

n=n₀+n₁2+n₂2²+…+n_m-12^m-1 （3.5.1）

式中，n_r取0或1（r=0，1，…，m-1）。

同样，任意k=0，1，…，N-1也可表示为

k=k₀+k₁2+k₂2²+…+k_m-12^m-1 （3.5.2）

式中，k_r取0或1（r=0，1，…，m-1）。变换基

根据离散傅里叶变换的定义

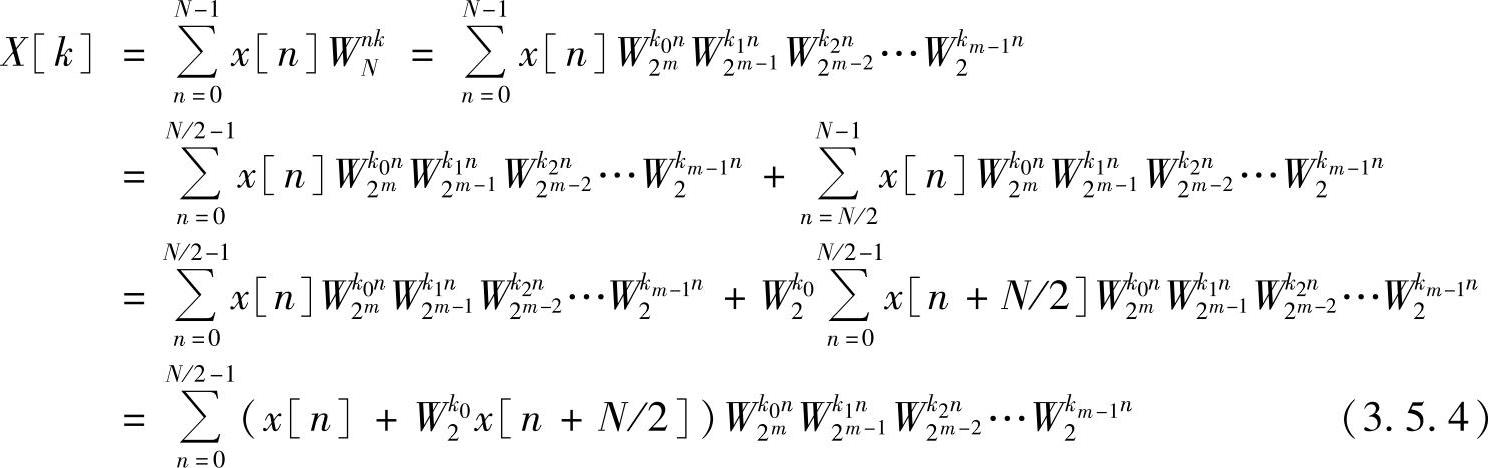
令

则

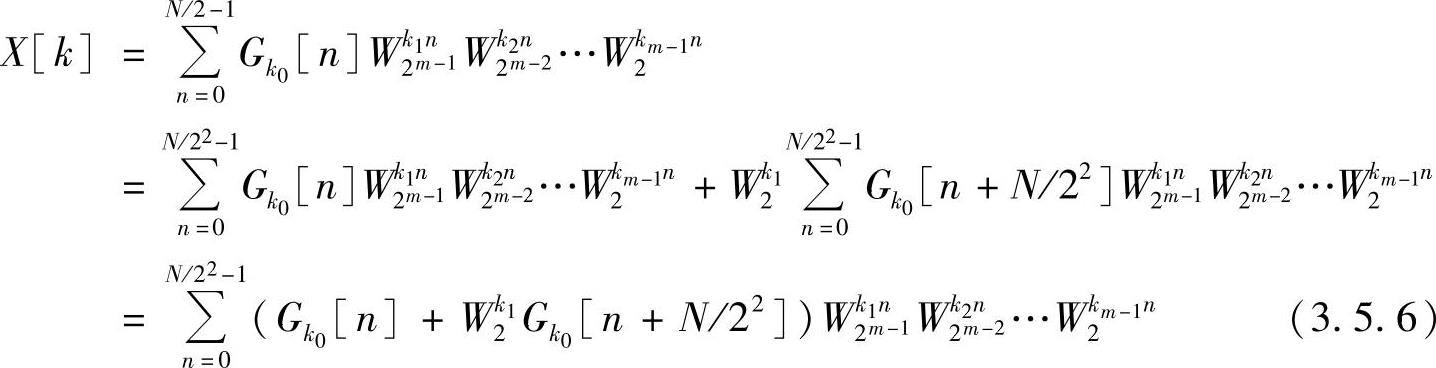
令

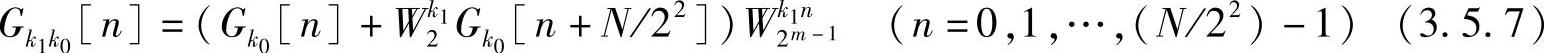
第l步分解得到

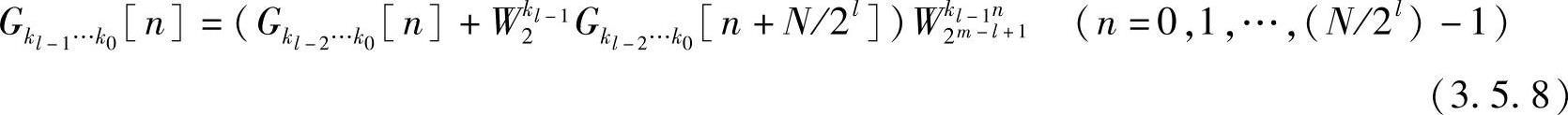
相应的基本蝶形图如图3.5.1所示，

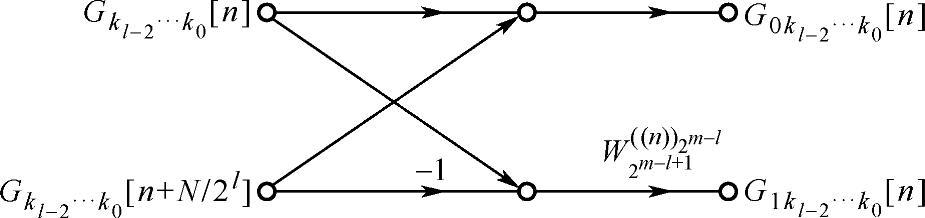
图3.5.1 DIF-FFT蝶形运算图(www.xing528.com)

图中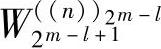，是旋转因子。

根据图3.5.1这个基本蝶形就可以画出任意2的整数次幂点数的快速傅里叶变换的完整的蝶形图。下面以8点为例，详细给出每一步的蝶形图和最终的蝶形图。8点快速傅里叶变换共需三步处理。

第一步：

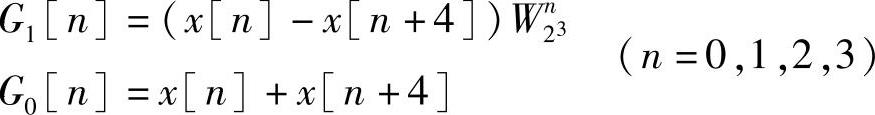
蝶形图如图3.5.2所示。

第二步：

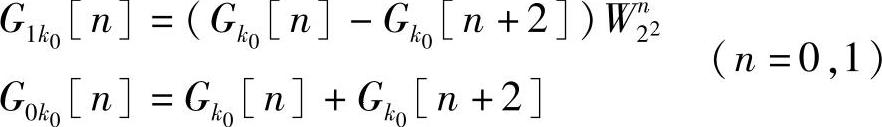
蝶形图如图3.5.3所示。

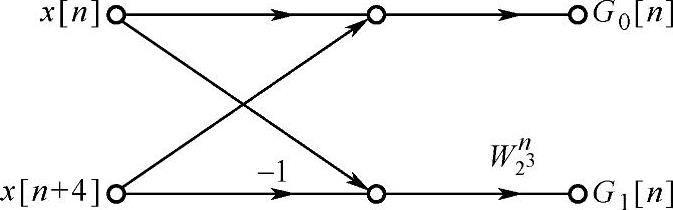
图3.5.2 N=8的第一步分解

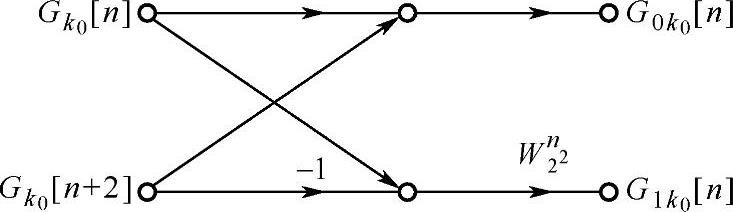
图3.5.3 N=8的第二步分解

第三步：

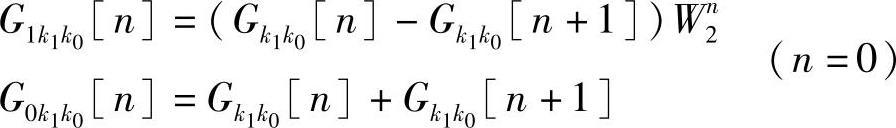
以上三步，每一步都要完成四个蝶形运算，完整的蝶形图如图3.5.4所示。

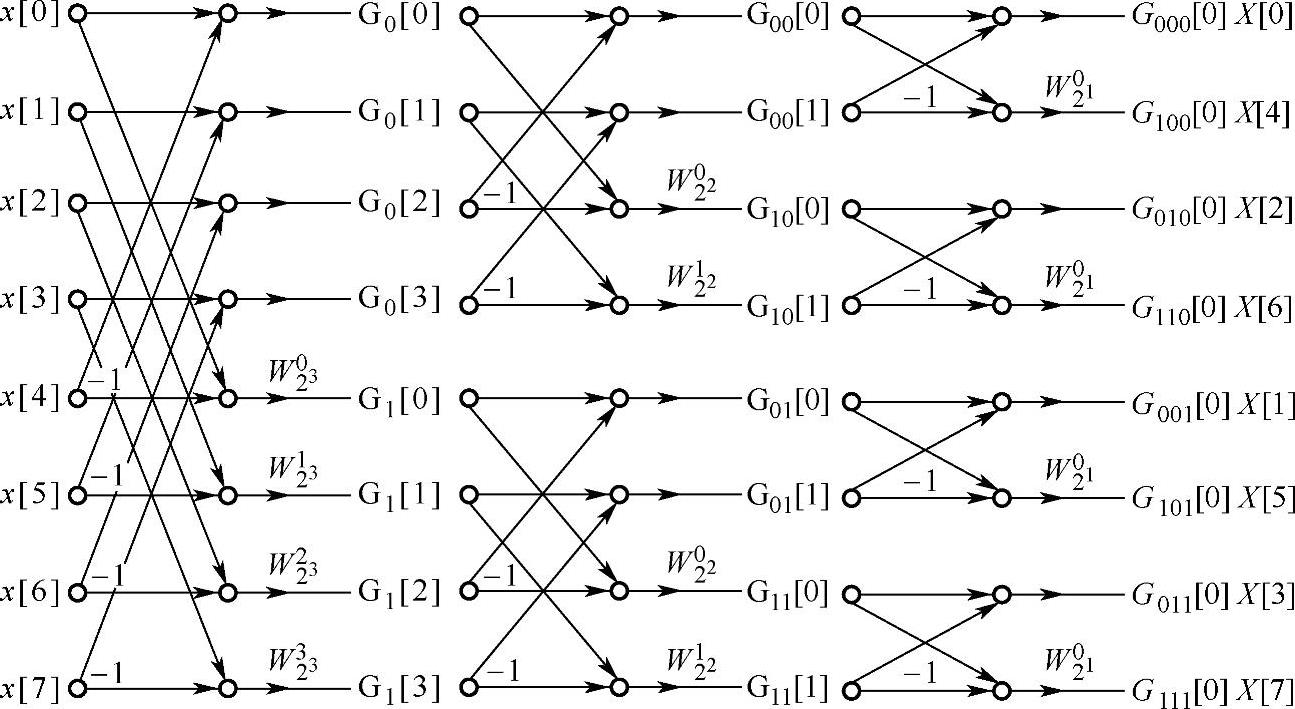
图3.5.4 N=8的第三步分解

可见输出是比特倒序的，最后一步序列的下标正好是k的二进制表示。与时间抽样快速傅里叶变换算法一样，也可以把蝶形重排变成输入倒序、输出正序的蝶形图。

对于N点快速傅里叶变换，上述过程一共要执行m=log₂N步，每步有N/2个蝶形运算，每个蝶形运算中需要一次复数乘法和两次复数加法，所以这种快速傅里叶变换算法所需要的计算量为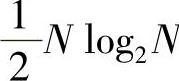次复数乘法和Nlog₂N次复数加法。