快速傅里叶变换算法基于频率抽取

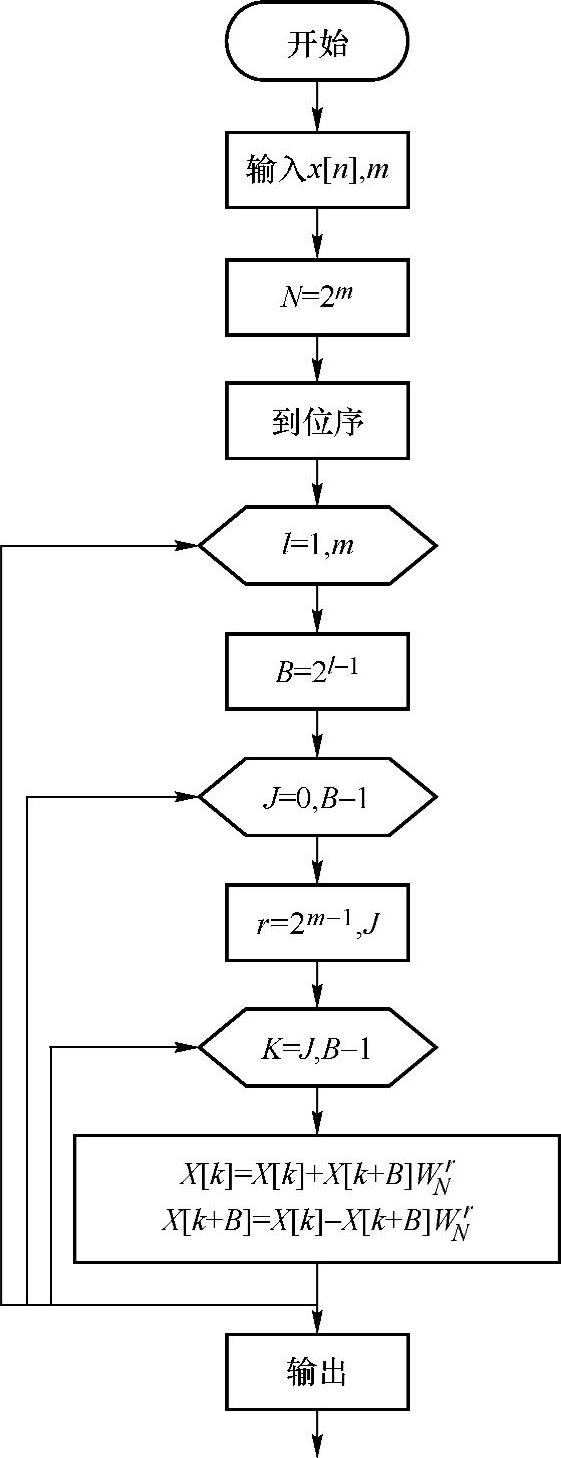
图3.3.5 DIT-FFT运算程序框图

除时间抽取法外，另外一种普遍使用的FFT结构是频率抽取法。频率抽取法将输入序列不是按奇、偶分组，而是将N点离散傅里叶变换写成前后两部分，即

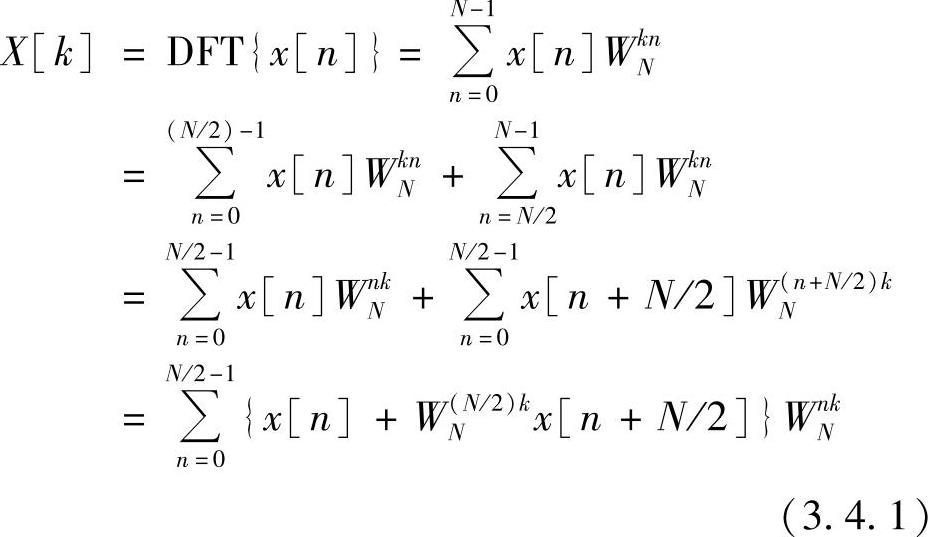
因为W^N_N/2=-1，W^（N/2）k_N=（-1）^k，k为偶数时（-1）k=1，k为奇数时（-1）^k=-1，由此可将X[k]分解为偶数组和奇数组，即

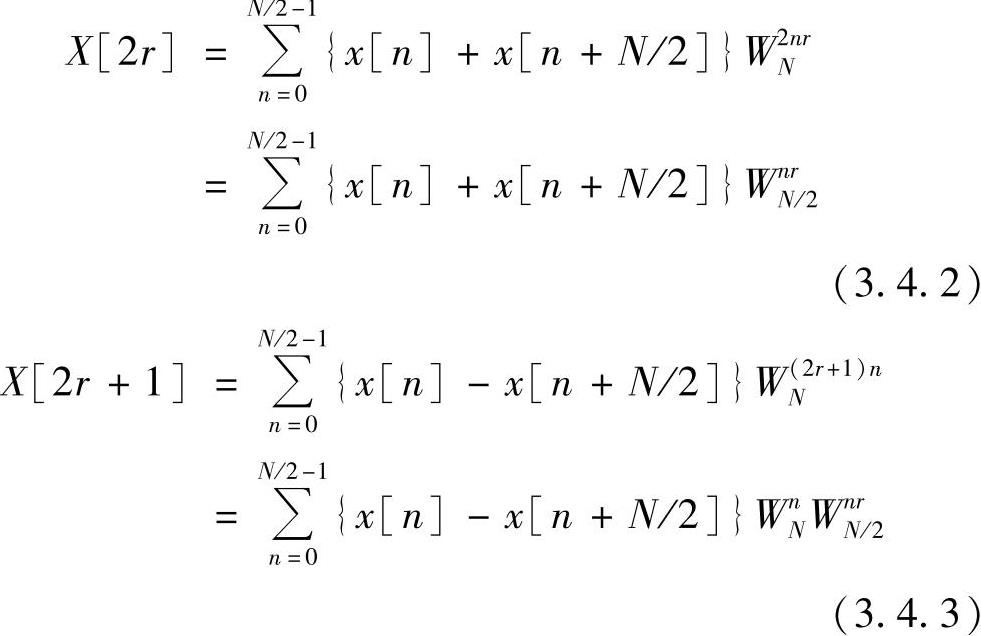
令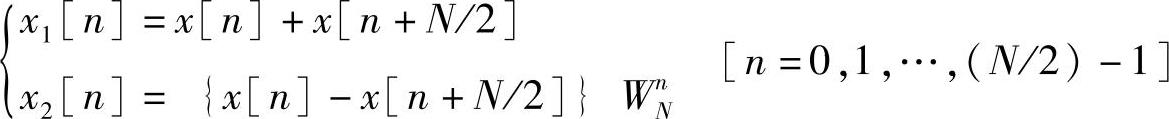

这两个序列都是N/2点的序列，对应的是两个N/2点的离散傅里叶变换运算，即

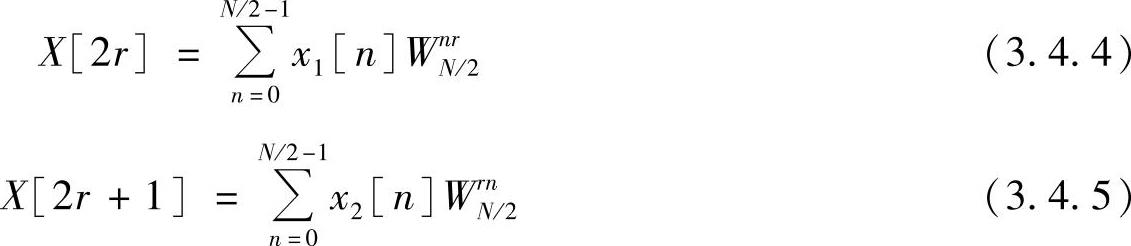
这样，同样是将一个N点的离散傅里叶变换分解为两个N/2点的离散傅里叶变换了。频率抽选法对应的蝶形运算符号如图3.4.1所示。

对于N=8时频率抽取法的快速傅里叶变换分解图和完整流图如图3.4.2所示。

这种分组的办法由于每次都是按输出X[k]在频域的顺序上是属于偶数还是奇数来分组的，称为频率抽取法。

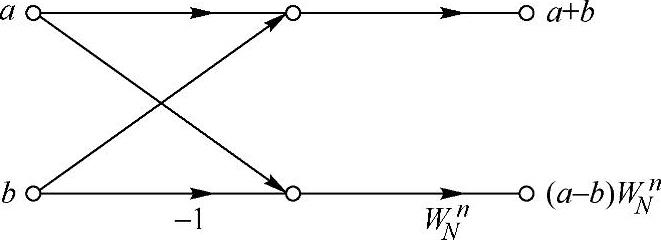
图3.4.1 频率抽取的蝶形运算符号

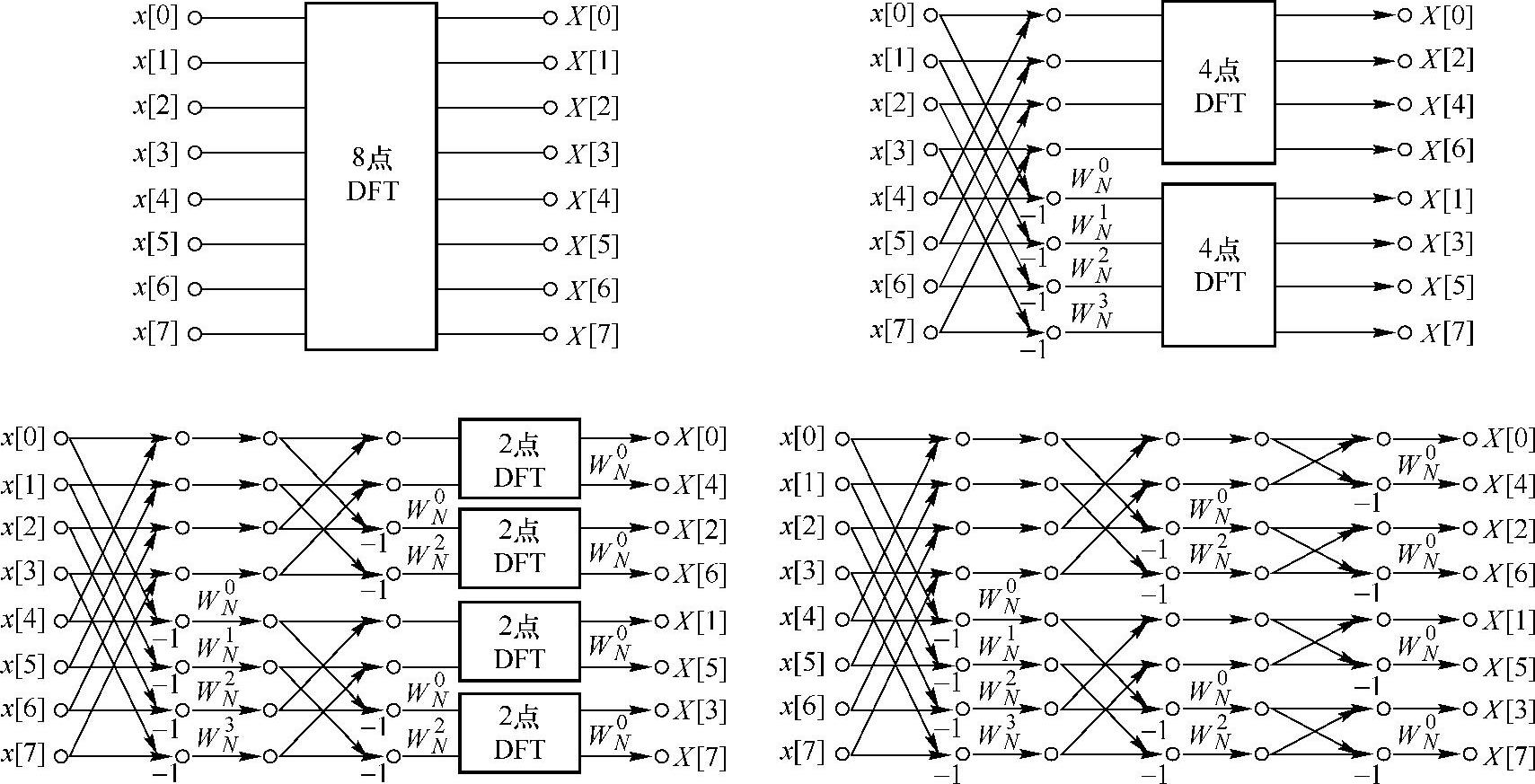
图3.4.2 8点DIF-FFT运算流图

与前面按时间抽取的方法相比，相同点是：

1）进行原位运算。

2）运算量相同，均为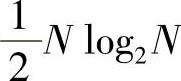次复数乘法和Nlog₂N次加法。(www.xing528.com)

不同点是：

1）时间抽取法输入为倒位序，输出为自然顺序；频率抽取法正好与此相反。但时间抽取法也有输入为自然顺序，输出为倒位序的情况。

2）蝶形运算不同。

①按时间抽取的蝶形图如图3.4.3所示。

②按频率抽取的蝶形图如图3.4.4所示。

将流图的所有支路方向都反向，交换输入和输出，即可得到另一种蝶形。前面描述了离散傅里叶变换的快速算法，那么如何利用快速算法计算离散傅里叶逆变换呢？

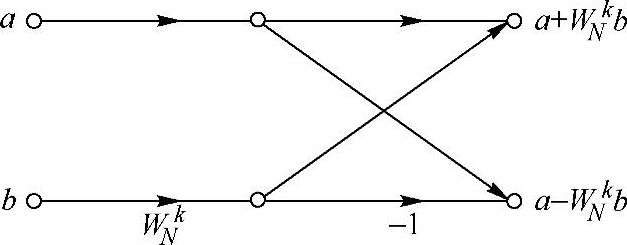
图3.4.3 按时间抽取的蝶形图

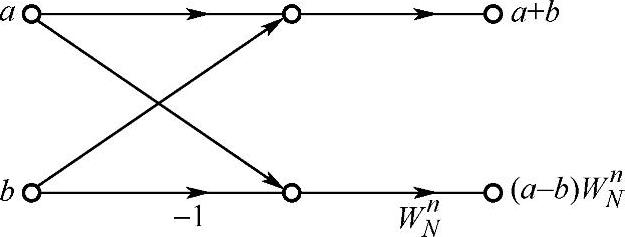
图3.4.4 按频率抽取的蝶形图

分析离散傅里叶逆变换的公式为

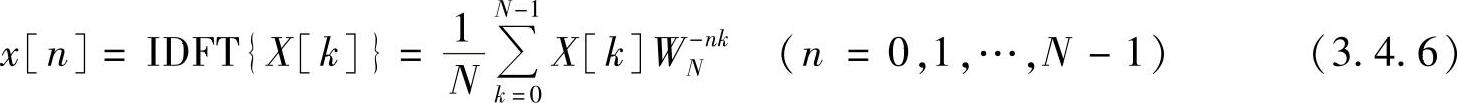
离散傅里叶变换的公式为

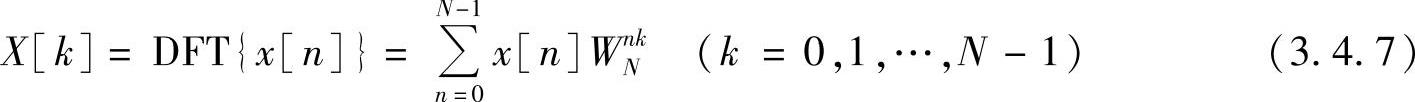
比较式（3.4.6）和式（3.4.7）得知可用两种方法来实现离散傅里叶逆变换的快速算法：

1）只要把离散傅里叶变换运算中的每一个系数W^nk_N改为W^-nk_N，并且最后再乘以常数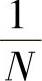，就可以用时间抽取法或频率抽取法的傅里叶变换的快速算法来直接计算离散傅里叶逆变换。这种方法需要对离散傅里叶变换的快速算法的程序和参数稍加改动才能实现。

2）因为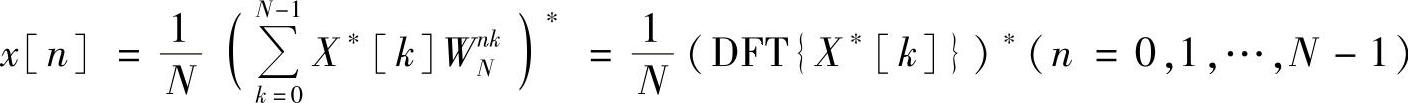，也就是说，可先将X[k]取共轭变换，即将X[k]的虚部乘以-1，就可直接调用离散傅里叶变换的快速算法的程序，最后再对运算结果取一次共轭变换并乘以常数1/N即可得到x[n]的值。这种方法中，快速傅里叶变换运算和快速傅里叶逆变换的运算都可以共用一个子程序块，在使用通用计算机或用硬件实现时比较方便。