快速傅里叶变换算法的时间抽取方法

为了将大点数的离散傅里叶变换分解为小点数的离散傅里叶变换运算，要求序列的长度N为复合数，最常用的是N=2^m（m为正整数）的情况。该情况下的变换称为基2快速傅里叶变换。下面讨论基2情况的算法。

先将序列x[n]按奇偶项分解为两组为

将离散傅里叶变换运算也相应分为两组为

其中X₁[k]、X₂[k]分别是x₁[n]、x₂[n]的N/2点的离散傅里叶变换，即

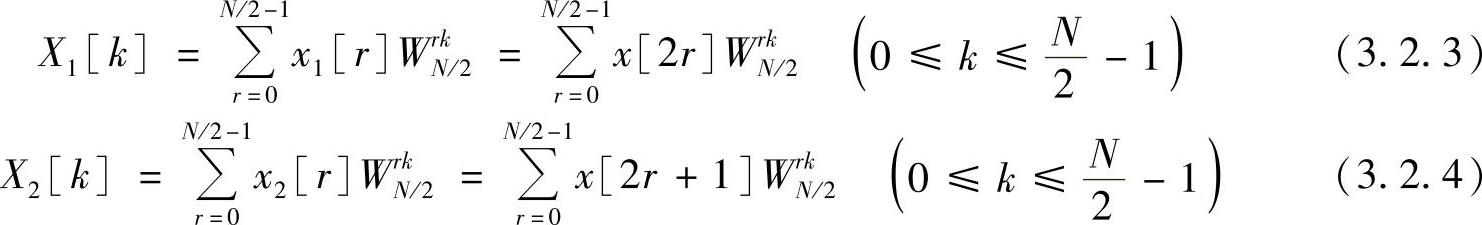
至此，一个N点离散傅里叶变换被分解为两个N/2点的离散傅里叶变换。

上面是否将全部N点的X[k]求解出来了？

分析：X₁[k]和X₂[k]只有N/2个点，则由X[k]=X₁[k]+W^k_NX₂[k]只能求出X[k]的前N/2个点的离散傅里叶变换，要求出全部N点的X[k]，需要找出X₁[k]、X₂[k]和X[k+N/2]的关系。由式（3.2.2）可得

X[k+N/2]=X₁[k+N/2]+W^k+N/2_NX₂[k+N/2]

化简得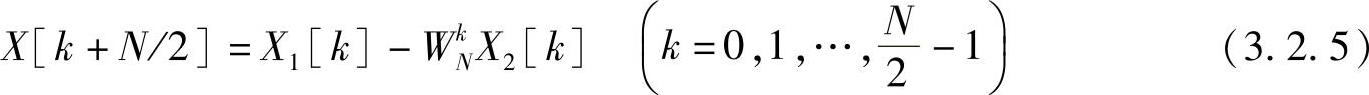

这样，N点离散傅里叶变换可全部由下式确定出来，即

式（3.2.6）可用一个专用的蝶形符号来表示，如图3.2.1所示，这个符号对应一次复数乘法和两次复数加法运算。

图3.2.1 蝶形运算符号

通过这样的分解以后，每一个N/2点的离散傅里叶变换只需要（N/2）2=N²/4次复数乘法，两个N/2点的离散傅里叶变换需要2（N/2）2=N²/2次复乘法，再加上将两个N/2点离散傅里叶变换合并成为N点离散傅里叶变换时有N/2次与W因子相乘，一共需要N²/2+N/2≈N²/2次复数乘法。可见，通过这样的分解，运算量节省了近一半。

因为N=2^m，N/2仍然是偶数，因此可以对两个N/2点的离散傅里叶变换再分别作进一步分解，将两个N/2点的离散傅里叶变换分解成两个N/4点的离散傅里叶变换。

例如对x₁[r]，可以再按其偶数部分及奇数部分进行分解，即

则运算可相应分为两组，即(www.xing528.com)

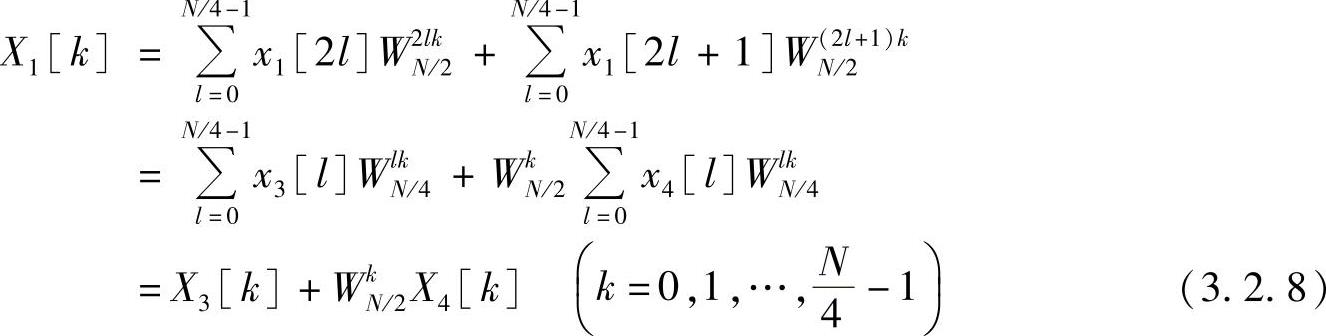
将系数统一为以N为周期，即W^k_N/2=W^2k_N，可得

同样，对X₂[k]也可进行类似的分解。一直分解下去，最后是2点的离散傅里叶变换，2点离散傅里叶变换的运算也可用蝶形符号来表示。这样，对于一个N=2³=8的离散傅里叶变换运算，其按时间抽取的分解过程及完整流图如图3.2.2所示。

这种方法，由于每一步分解都是按输入序列在时域上的次序是属于偶数还是奇数来抽取的，故称为“时间抽取法”。

分析图3.2.2，N=2^m，一共要进行m次分解，构成了从x[n]到X[k]的m级运算过程。每一级运算都是由N/2个蝶形运算构成，因此每一级运算都需要N/2次复乘和N次复加，则按时间抽取的m级运算后总共需要

复数乘法次数：

复数加法次数：

根据图3.2.2，分析快速傅里叶变换算法有两个特点，它们对快速傅里叶变换的软硬件构成产生很大的影响。

1.原位运算

也称为同址运算，当数据输入到存储器中以后，每一级运算的结果仍然存储在原来的存储器中，直到最后输出，中间无须其他的存储器。原位运算的结构可以节省存储单元，从而降低设备成本。

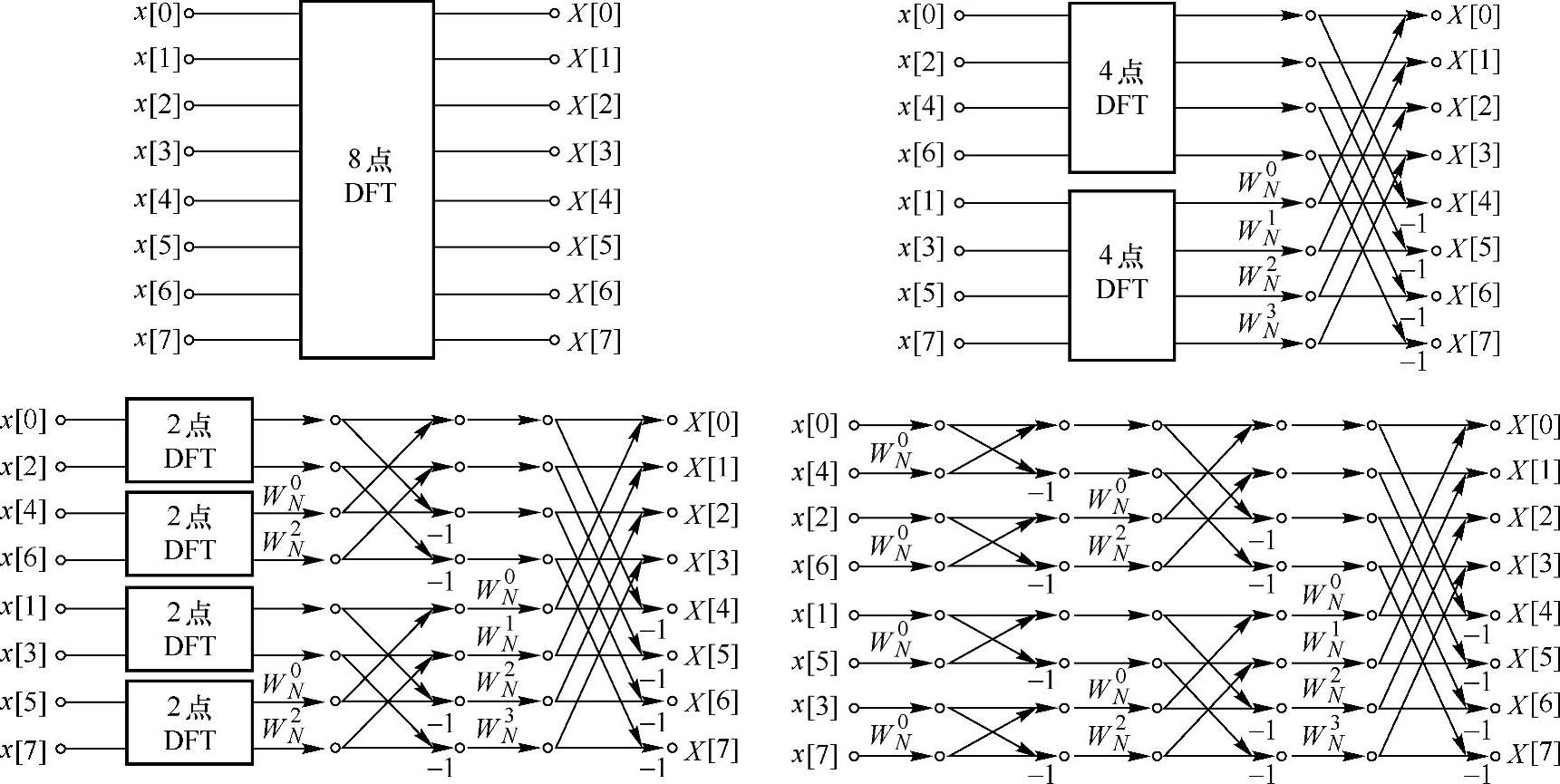
图3.2.2 8点DIT-FFT运算流图

2.变址

分析运算流图中的输入输出序列的顺序，输出按顺序，输入是“码位倒置”的顺序，见表3.2.1。

表3.2.1 顺序和倒序二进制数对照表

在实际运算中，直接将输入数据x[n]按码位倒置的顺序排好输入很不方便，一般总是先按自然顺序输入存储单元，然后通过变址运算将自然顺序的存储换成码位倒置顺序的存储，这样就可以进行快速傅里叶变换的原位运算。变址处理如图3.2.3所示。用软件实现时通常采用雷德（Rader）算法，算出I的倒序J以后立即将输入数据X[I]和X[J]对换。尽管变址运算所占运算量的比例很小，但对某些高要求的应用（尤其在实时信号处理中），也可设法用适当的电路结构直接实现变址。例如单片数字信号处理器TMS320C25就有专用于快速傅里叶变换的二进制码变址模式。

图3.2.3 码位倒置的变址处理

图3.2.4是实现倒位序的框图。其中点画线框内的流程图是对J进行的逆记数部分，所谓逆记数就是每次最高位加1，逐次向低位进位。最高位加1相当于十进制数运算为J+N/2，如果最高位是0（J＜N/2），则直接由J+N/2得一个倒序值；如果最高位是1（J≥N/2），则将最高位变为0（J=J-N/2）。用同样的方法判断次高位，如果次高位是0（J＜N/4），则直接加1（J=J+N/4），否则将次高位变为0（J=J-N/4）。再判断下一位，依次类推，直到完成最高位加1，向右进位的运算。