使用离散傅里叶变换分析连续信号的频谱

用离散傅里叶变换对连续信号进行频谱分析的基本步骤如图2.7.1所示。当连续时间信号转换为一个序列时，需要加入抗混叠滤波器以消除混叠的影响，或者将它减小到最低程度。需要用w[n]乘以x[n]，即作加窗处理，这是离散傅里叶变换要求有限长度的必然结果。在许多实际应用中，s_c（t）很长，甚至无限长。自然x[n]也如此（如语音和音乐的情况）。因此，在计算离散傅里叶变换之前，需要将有限长度的窗w[n]加到x[n]上。图2.7.2说明了图2.7.1中的信号的傅里叶变换。具体讲，图2.7.2a表示一个连续时间谱，它在高频区有逐渐减小的拖尾，而不是带限的，图中窄的尖锐谱峰还表明存在着一些窄带信号的能量。图2.7.2b表示抗混叠滤波器的频率响应。正如图2.7.2c所指出的，得出的连续时间傅里叶变换X_c（jΩ）几乎不包含有S_c（jΩ）在滤波器截止频率以上部分的有用信息。因为H_aa（jΩ）不可能是理想的，所以输入信号在通带和过渡带的傅里叶频率成分也将受到滤波器频率响应的影响。

图2.7.1 连续时间信号的离散时间傅里叶分析的处理步骤

x_c（t）向样本序列x[n]的转换，可在频率上用周期重复和归一化来表示，即

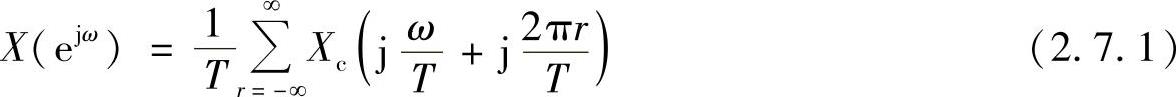
如图2.7.2d所示。由于实际实现中抗混叠滤波器不可能再阻带有无线衰减，因此可以预见，式（2.7.1）中的项会有一些非零重叠，即混叠。但是用一个高质量的连续时间滤波器，或者使用初始过采样，接着通过十分有效的低通滤波和抽取，均可以将这一误差减小到可以忽略的程度。如果x[n]是数字信号，则图2.7.1中的连续-时间转换（A-D转换）可以合并到第二个系统中去，但仍会引入量化误差。这种误差可以作为噪声序列加到x[n]上。这种噪声也可以通过精细的量化而忽略不计。

因为离散傅里叶变换的输入信号必须是有限长的，所以通常是用有限长窗w[n]乘以序列x[n]。这就产生了有限长序列v[n]=w[n]x[n]。它在频域上表现为周期卷积，即

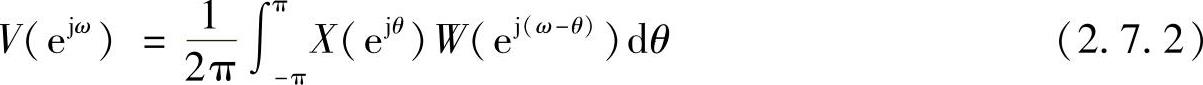
图2.7.2e表示一种典型窗序列的傅里叶变换。注意，一般总是假设主瓣集中在ω=0附近。若在n的某一范围内w[n]为非零数，则称其为矩形窗。但是，我们将会看到，有充分的理由使窗函数在其边缘处呈拖尾状。如像Bartlett窗、Hamming窗、Hanning窗、Blackman窗及Kaiser窗等窗函数的性质将在第6章中讨论，从这一点上必然会看到，W（e^jω）与X（e^jω）的卷积将对X（e^jω）中的尖峰和不连续点起平滑作用。在图2.7.2f中，这种现象用连续的曲线表示出来。

图2.7.1中最后的运算是离散傅里叶变换，加窗序列v[n]=w[n]x[n]后的离散傅里叶变换为

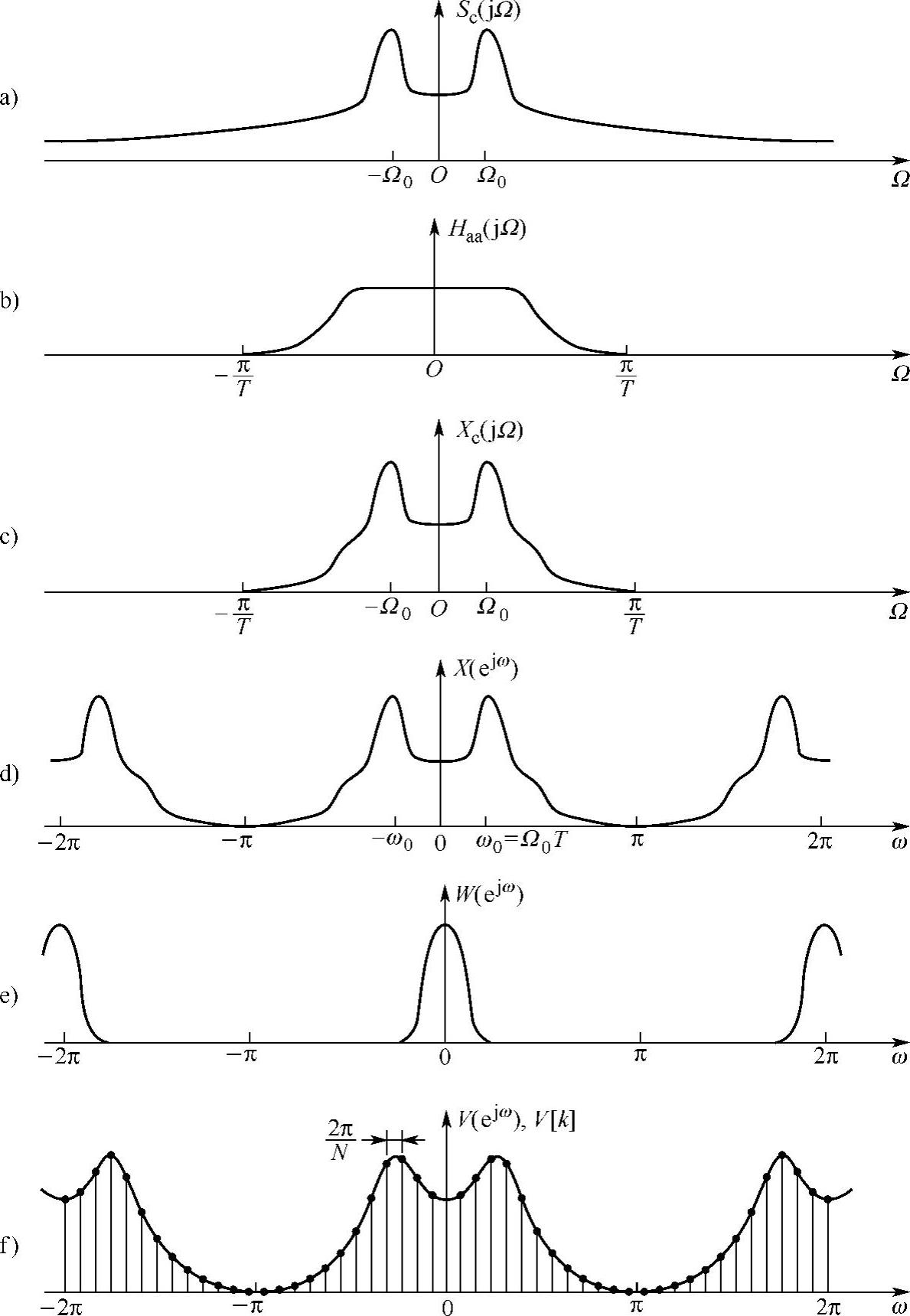
图2.7.2 加抗混叠滤波器的频谱分析过程

a）连续时间输入信号的傅里叶变换 b）抗混叠滤波器的频率响应 c）抗混叠滤波器输出的傅里叶变换 d）采样信号的傅里叶变换 e）窗序列的傅里叶变换 f）加窗信号段的傅里叶变换和用DFT样本得到的频率样本

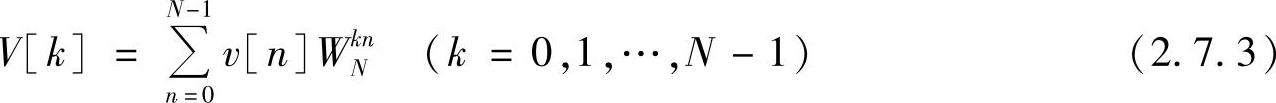
式中，假设窗的长度N₁小于或等于离散傅里叶变换的长度N。有限长序列υ[n]的离散傅里叶变换V[k]对应于υ[n]的离散时间傅里叶变换的等间隔采样，即

V[k]=V（e^jω）∣_ω=2πk/N （2.7.4）

图2.7.2f还说明V[k]是V（e^jω）的样本。因为离散傅里叶变换相邻频率间的间隔为，且归一化离散时间频率变量和连续时间变量之间的关系是ω=ΩT，所在离散傅里叶变换的频率

对应于连续时间频率

许多商用实时谱分析仪就是基于图2.7.1和图2.7.2中所包含的原理。然而，由上面的讨论可以清楚地看出，利用加窗采样信号段离散傅里叶变换来解释输入信号的连续时间傅里叶变换，会受到许多因素的影响。考虑到这些因素，在对输入信号滤波和采样时必须十分小心。因此，要能够正确地解释所得出的结果，必须清楚地理解在离散傅里叶变换中固有的时域加窗和频域采样的影响。对于后面的讨论，假设抗混叠滤波和连续时间到离散时间的转换工作均已完成，并可不再考虑。下一节将特别集中讨论由离散傅里叶变换所带来的加窗和频域采样的影响。虽然选择正弦信号作为所讨论的典型例子，但是所讨论到的大部分问题均具有普遍性。

【例2.7.1】 设一个带限连续信号x_c（t），当Ω≥2π时X_c（jΩ）=0，利用图2.7.1中的系统来估计连续时间谱X_c（jΩ）。假设抗混叠滤波器H_aa（jΩ）是理想的，且连续时间到离散时间（C/D）转换器的采样率为1/T=5000Hz。如果要使离散傅里叶变换V[k]等于X_c（jΩ）的样本，且相邻样本间隔最多为2πrad/s，那么所用的离散傅里叶变换样本数N的最小值应为多少？(www.xing528.com)

解 由式（2.7.5）可知，离散傅里叶变换中相邻的样本对应的间隔是2π/（NT）的连续时间频率。因此，要求

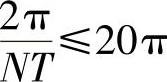
于是

N≥500

便可满足条件。

【例2.7.2】 在例2.7.1中，1/T=5000Hz，N=512，且x_c（t）的值为实数，并充分带限以避免在给定采样频率下混叠。如果给定V[11]=2000（1+j），则V[k]或X_c（jΩ）的其他值是多少？

解 根据对称性有

V[k]=V^∗[（（-k））_N] （k=0，1，…，N-1）

而且

V[N-k]=V^∗[k]

所以

V[512-11]=V[501]=V^∗[11]=200（1-j）

离散傅里叶变换样本点k=11对应于连续时间频率

Ω₁₁=2π×11×5000/512=2π×107.4

同样，k=501对应于连续时间频率

-2π×11×5000/512=-2π×107.4

虽然加窗可使频谱平滑，但可以认为

X_c（jΩ₁₁）=X_c（j2π×107.4）≈TV[11]=0.4（1+j）

式中，因子T是用于补偿由采样所引入的因子1/T，再次利用对称性，可以最后得出

X_c（-jΩ₁₁）=X_c（-j2π×107.4）≈TV^∗[11]=0.4（1-j）。