用离散傅里叶变换实现线性移不变系统的方法

以上讨论了从循环卷积得到线性卷积的方法。因为线性移不变系统可以用卷积来实现，这就意味着循环卷积可用来实现这类系统。要了解如何做到这一点，首先考虑一个N₁点输入序列x[n]和一个N₂点单位抽样响应h[n]。这两个序列的线性卷积y[n]是长度为（N₁+N₂-1）的有限长序列。因此，正如上节所讨论的，要使循环卷积等于线性卷积，循环卷积的长度至少为（N₁+N₂-1）点。循环卷积可以通过x[n]和h[n]的离散傅里叶变换相乘来完成。由于希望该乘积表示x[n]和h[n]的线性卷积的离散傅里叶变换，该离散傅里叶变换的长度为（N₁+N₂-1），因此所要计算的离散傅里叶变换也必须有同样的长度，即x[n]和h[n]必须加长，而加长部分的序列值为零。这种方法通常称为补零。

这种做法使两个有限长序列的线性卷积的计算可用离散傅里叶变换来完成，在许多应用场合（如语音波形滤波），输入信号是无限长的。尽管理论上可以储存全部波形，紧接着对于大量点数实行上面所讨论的利用离散傅里叶变换的方法，但是通常要计算这样一个离散傅里叶变换是不现实的。另外对于这种滤波方法，只有当采集完全部的输入样本后才能计算出滤波后的样本。一般说来，总希望在处理过程中避免这种很长的延时。这两个问题的解决方法是用块卷积，此时把被滤波的信号分割成长度为N₁的段。然后每段信号就可以与有限长单位抽样响应进行卷积，并且用一种适当的方法把滤波后的信号段衔接在一起。每一块的线性滤波可以用离散傅里叶变换来实现。

为了举例说明这一过程，并且得出把滤波后的信号段衔接在一起的方法，我们来研究如图2.6.5所示长度为N₂的单位抽样响应h[n]和未定义长度的信号x[n]。假设对于n＜0，x[n]=0，并且x[n]的长度要比N₂大许多。序列x[n]可以表示成长度为N₁的平移有限长序列之和，即

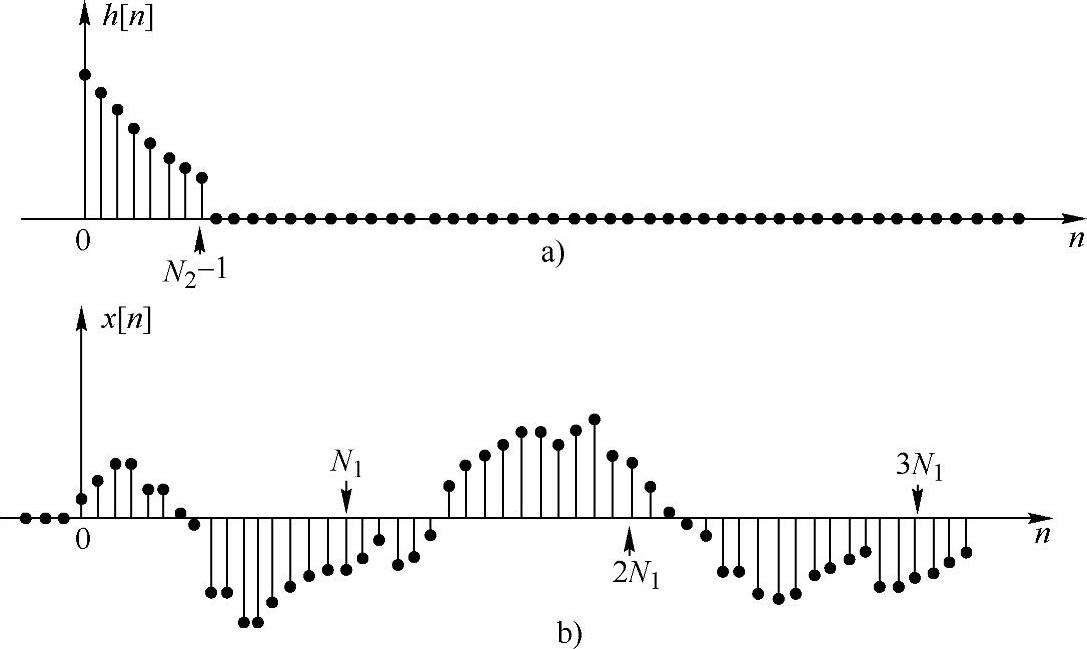
图2.6.5 参与运算的两个信号

a）有限长单位抽样响应h[n] b）未定义长度的输入信号x[n]

式中

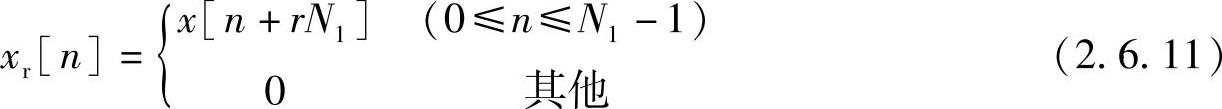
图2.6.6a表示出对图2.6.5中x[n]的分割方法。注意，每段中的第一个样本均在n=0处，然而，x_r[n]的第零个样本是序列x[n]的第rN₁个样本。这一点如图2.6.6a所示，该图中画出了在它们平移后位置上的序列段。

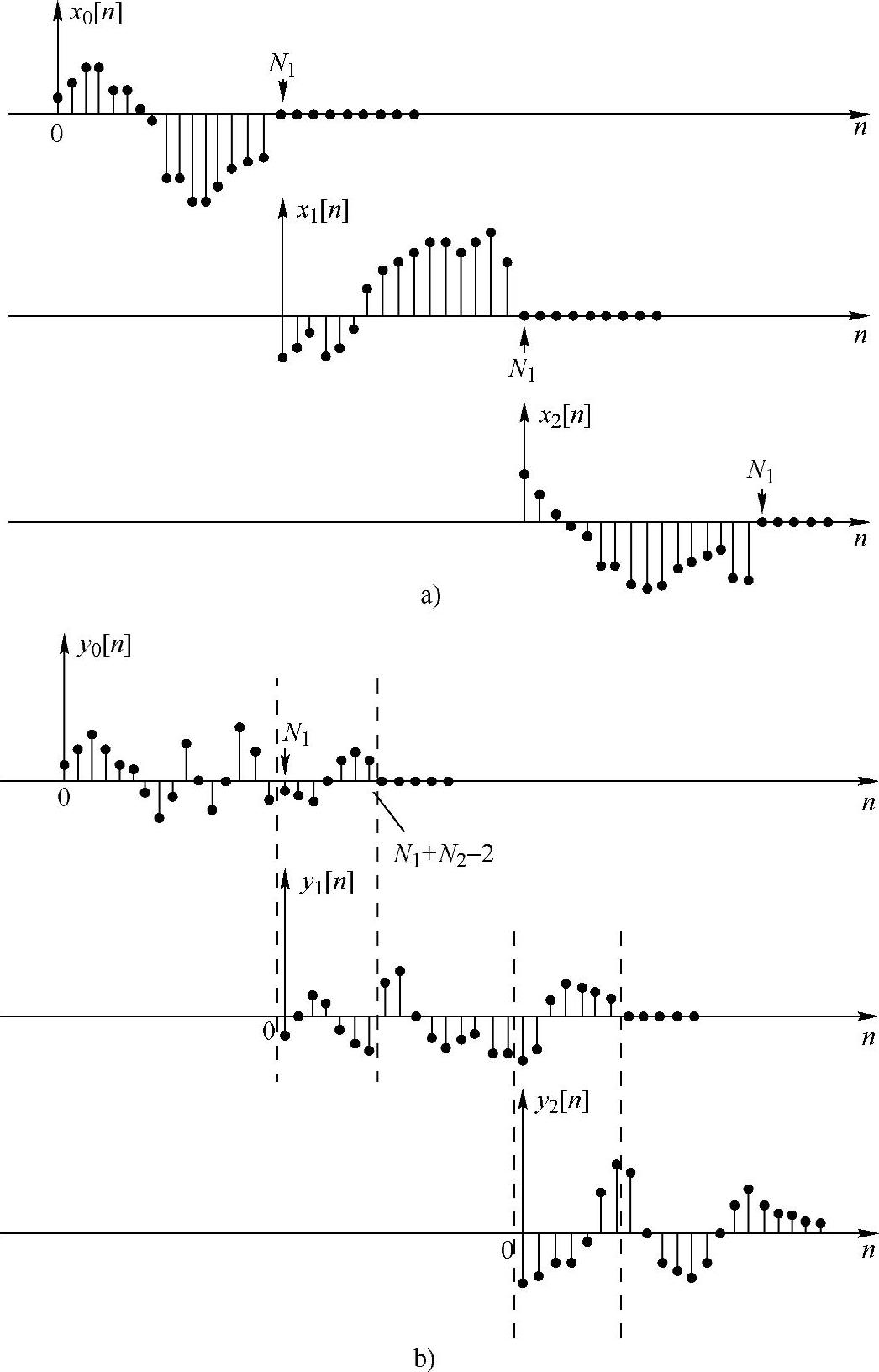
图2.6.6 重叠相加法运算过程

a）x[n]分解为长度为N₁的不重叠序列段 b）每段与h[n]卷积的结果

因为卷积是一种线性移不变运算，所以由式（2.6.10）有

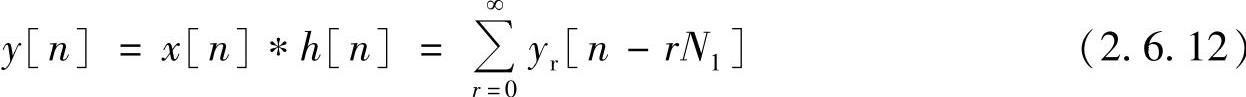
式中(www.xing528.com)

y_r[n]=x_r[n]∗h[n] （2.6.13）

由于序列x_r[n]只有N₁个非零点，并且h[n]的长度为N₂，因此每一项y_r[n]=x_r[n]∗h[n]的长度为（N₁+N₂-1）。这样，线性卷积x_r[n]∗h[n]可以用N点离散傅里叶变换按照上面介绍的步骤来计算，其中N≥N₁+N₂-1。因为每个输入段的开头与相邻段相隔N₁点，并且每个滤波后的序列段的长度为（N₁+N₂-1），所以滤波后的序列段的非零点将重叠（N₂-1）点，并且这些重叠样本必须参与式（2.6.12）要求的求和运算。这一点如图2.6.6b所示，图中表示出滤波后的序列段y_r[n]=x_r[n]∗h[n]。正如输入波形是将图2.6.6a中的延迟波形相加而重构成的一样，滤波后的结果x_r[n]∗h[n]是将图2.6.6b中滤波后延迟的序列段相加而形成的。这种由滤波后的序列段形成滤波后输出序列的方法，通常称为重叠相加法，这是因为滤波后的序列段相互有重叠，并且相加在一起形成输出序列。之所以发生重叠，是因为每个序列段与单位抽样响应的线性卷积通常大于序列段长度。块卷积的重叠相加法没有受离散傅里叶变换和循环卷积的制约。很显然，唯一的要求是计算较小的卷积，并将结果适当组合。

另外一种块卷积方法通常称为重叠保留法。这种方法是实现一个N₂点单位抽样响应h[n]与一个N₁点的序列段x_r[n]的N₁点循环卷积，然后确认出在该循环卷积中对应于线性卷积的那一部分。最后将所得出的输出序列段“补在一起”形成输出序列。特别是如果一个N₁点的序列与一个N₂点的序列（N₂＜N₁）做循环卷积，则最后结果中的第一个（N₂-1）点是不正确的，而其余点等于执行一个线性卷积所得到的值。因此，可以将x[n]分为长度为N₁的序列段，使得每个输入段与先前的序列段重叠（N₂-1）点。也就是说，定义序列段为

x_r[n]=x[n+r（N₁-N₂+1）-N₂+1] （0≤n≤N₁-1） （2.6.14）

和前面一样，式（2.6.14）中已经定义了每个序列段的时间原点是在该序列段的起始点处，而不是在x[n]的原点。这种分段的方法绘于图2.6.7a中，每个序列段与h[n]的循环卷积记做y_rp[n]，下标中的p表示y_rp[n]是已经产生了时间混叠的循环卷积的结果。在图2.6.7b中绘出了这些序列。每个输出序列段在区间0≤n≤N₂-2中的部分是必须去掉的。最后把来自后续序列段的其余样本邻接起来构成最终的滤波输出。即

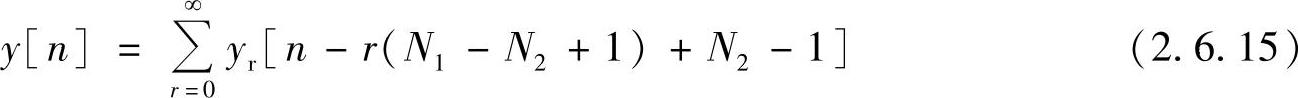
式中

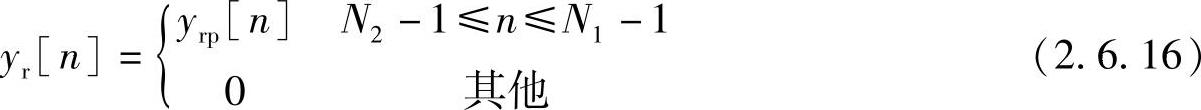
这种方法称为重叠保留法，因为输入序列段有重叠，所以每个接续的输入序列包括有（N₁-N₂+1）个新点，并且从先前的序列段保留下来（N₂-1）个点。

下一章，将学习离散傅里叶变换的高效算法，这些算法通称为快速傅里叶变换（Fast Fourier Transform，FFT），它们是十分有效的，对于平坦的适当长度的有限冲激响应，用离散傅里叶变换来计算块卷积可能要比直接计算线性卷积更有效。当然，确定使离散傅里叶变换方法更有效的长度N₂与进行计算可利用的硬件和软件有关。

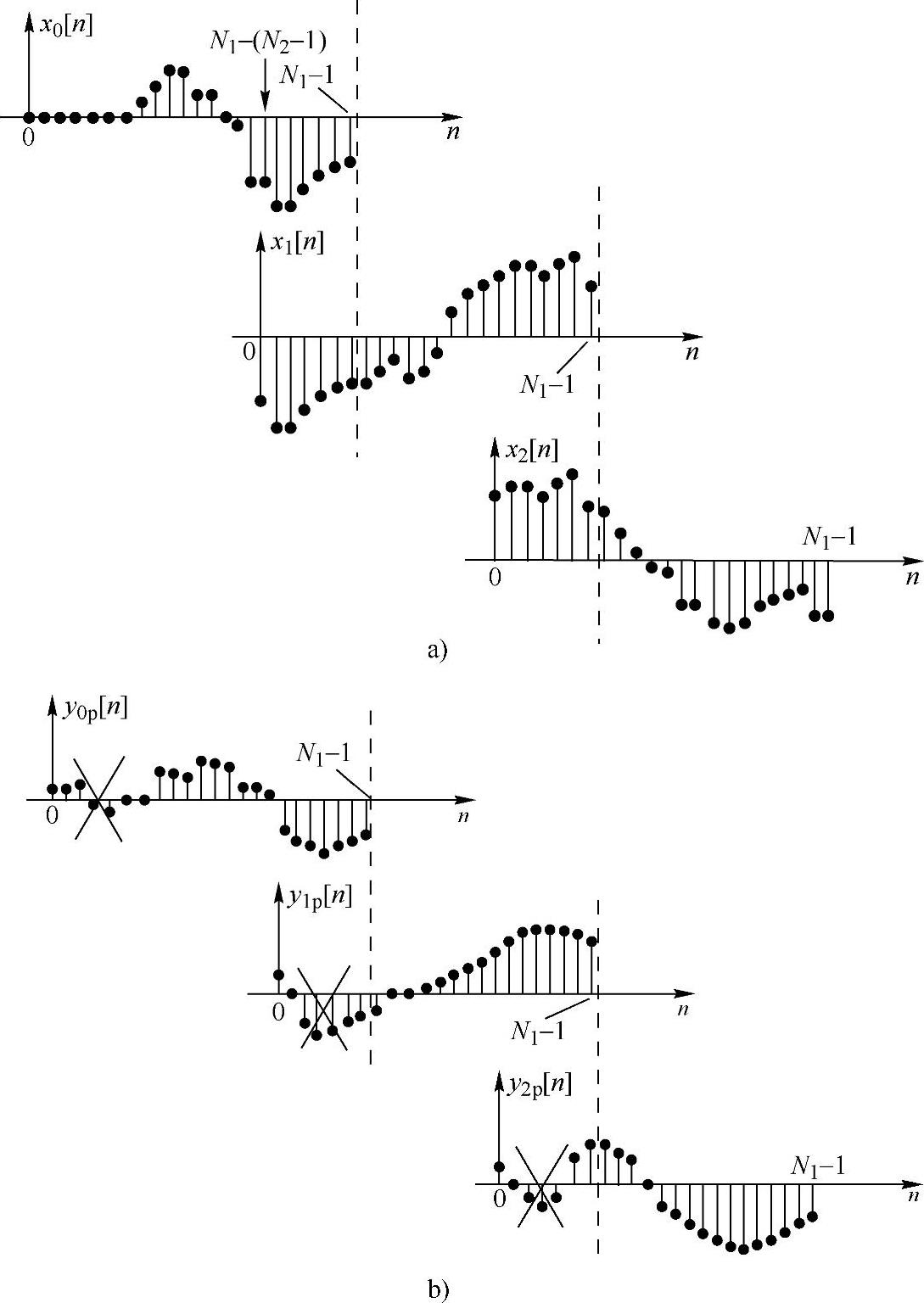
图2.6.7 重叠保留法运算过程

a）x[n]分解为相互重叠的长度为N₁的序列 b）每段与h[n]卷积的结果

注：为了得到线性卷积，图中“×”表示滤波后每段序列应当去掉的部分。