改写后：混叠现象在循环卷积中的应用

正如在例2.5.3看到的，对应于两个N点的离散傅里叶变换的乘积的循环卷积，是否与对应的有限长序列的线性卷积相同，取决于离散傅里叶变换的长度。循环卷积是带有混叠的线性卷积，下面分几种方式来讨论它们之间的这种关系。

如果对一个序列x[n]的傅里叶变换X[e^jω]在频率ω_k=2πk/N处采样，则得到对应于周期序列

的离散傅里叶级数的系数序列。从关于离散傅里叶变换的讨论中可以看出

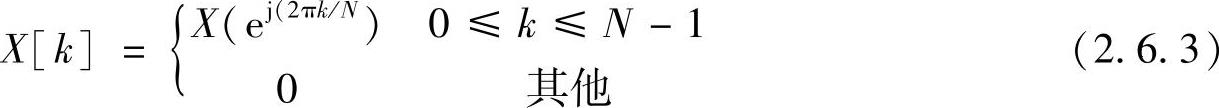
式（2.6.3）是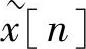的一个周期的离散傅里叶变换，设X[k]的逆变换为x_p[n]，则

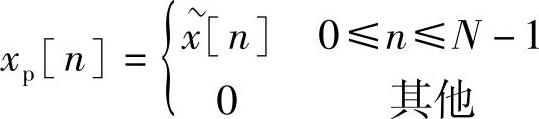
显然，如果x[n]的长度小于等于N，则不会产生时间混叠，即x_p[n]=x[n]。但是，若x[n]的长度大于N，则对于一些或全部n，x_p[n]可能不等于x[n]。因此，以后将用下标p来表示从一个采样后的傅里叶变换的逆变换得到周期序列的一个周期。如果明确知道无时间混叠，则下标可以省略。

式（2.6.1）的序列x₃[n]的离散时间傅里叶变换为

X₃（e^jω）=X₁（e^jω）X₂（e^jω） （2.6.4）

若定义一个离散傅里叶变换为

X₃[k]=X₃（e^{j（2πk/N）}） （0≤k≤N-1） （2.6.5）

于是

X₃[k]=X₁（e^{j（2πk/N）}）X₂（e^{j（2πk/N）}）=X₁[k]X₂[k]（0≤k≤N-1） （2.6.6）

则，X₃[k]的离散傅里叶逆变换x_3p[n]为

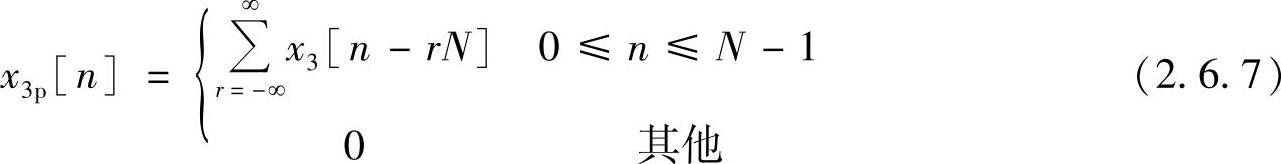
由式（2.6.6）可得

(www.xing528.com)

从式（2.6.7）和式（2.6.8）可以看出，两个有限长序列的循环卷积等于有时间混叠的两个序列的线性卷积。

应当注意，若N大于或等于N₁或N₂，则X₁[k]和X₂[k]可以完全表示x₁[n]和x₂[n]，但是只有当N大于或等于x₃[n]的长度时，才可能对全部n有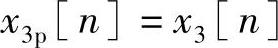。正如2.6.1节所指出的那样，如果x₁[n]的长度为N₁，x₂[n]的长度为N₂，则x₃[n]的最大长度为（N₁+N₂-1）。因此，若离散傅里叶变换的长度N满足N≥N₁+N₂-1，则对应于X₁[k]X₂[k]的循环卷积等于X₁（e^jω）X₂（e^jω）对应的线性卷积。

为说明循环卷积作为带有混叠的线性卷积，下面以长度为6（N₁=N₂=6）的两个完全相同的矩形序列，即x₁[n]=x₂[n]=R₆[n]（见图2.6.2a）为例进行讨论。

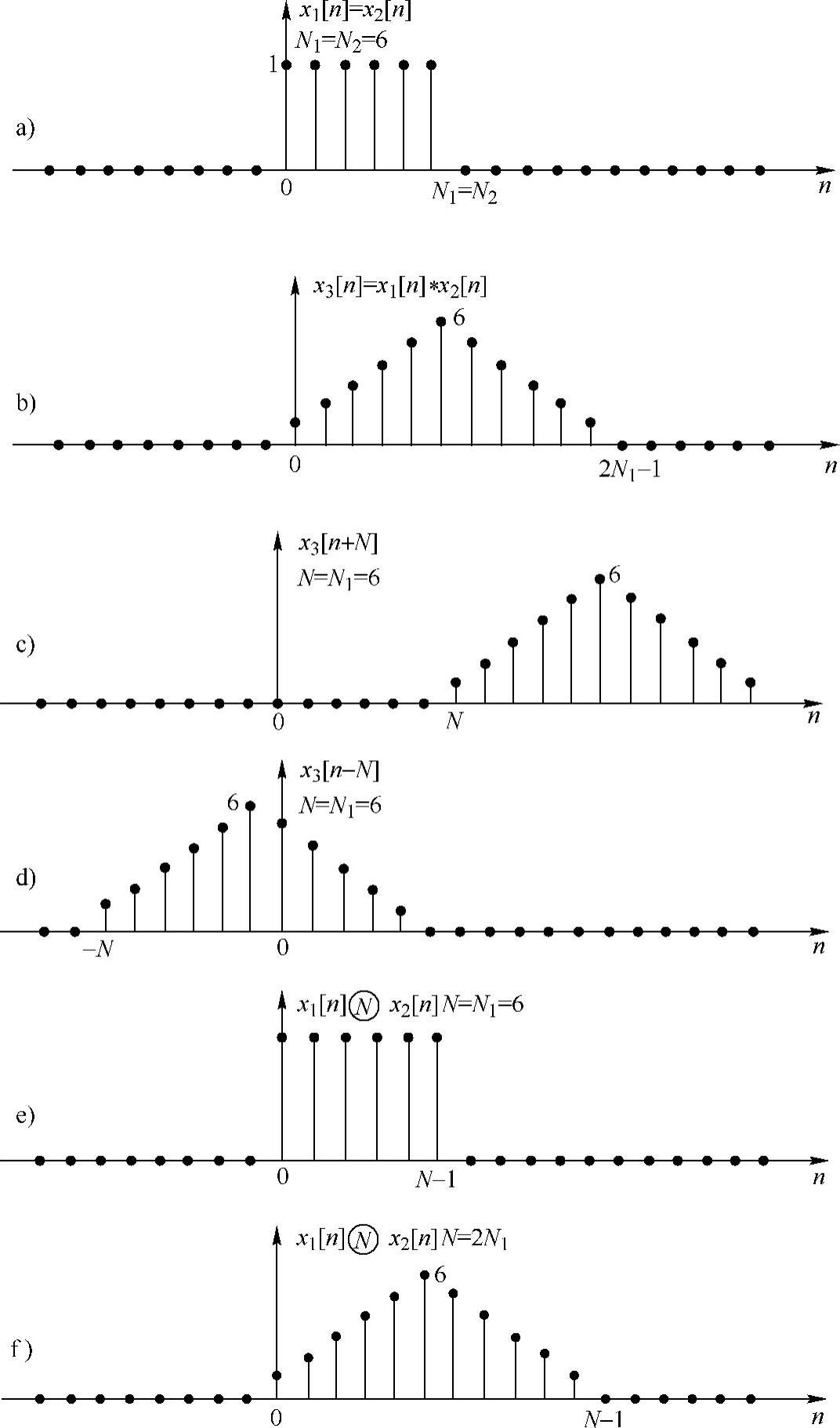
图2.6.2 循环卷积等同于有混叠的线性卷积

从上述讨论的几种情况可以看到，x₁[n]和x₂[n]线性卷积长度为N₁+N₂-1=11，且具有三角性的包络，如图2.6.2b所示。图2.6.2c、d表示当N=6时，线性卷积x₃[n]的两种移位序列x₃[n-N]和x₃[n+N]。利用式（2.6.7）计算x₁[n]和x₂[n]的N=N₁=6点循环卷积如图2.6.2e所示，N=2N₁=12点循环卷积如图2.6.2f所示。需要注意，当N=N₁=6时，只有x₃[n]和x₃[n+N]对最后的结果有贡献；而当N=2N₁=12时，仅x₃[n]对最后的结果有贡献。由于线性卷积的长度为（2N₁-1），所以当N=2N₁时，其循环卷积结果与线性卷积的结果对全部0≤n≤N-1均相同。事实上，对于N=2N₁-1=11的情况也是完全正确的。

显然，如果N=N₁=N₂，则循环卷积的全部序列值可以完全与线性卷积的值不同。但是，若N₂＜N₁，则N₁点循环卷积的部分序列值将会等于线性卷积所对应的值。为了表示出这一点，用时间混叠来解释是十分清晰的。

下面研究两个有限长序列x₁[n]和x₂[n]，其长度分别为N₁和N₂，如图2.6.3a、b所示，其中N₂＜N₁。首先讨论x₁[n]和x₂[n]的N₁点循环卷积，查看在循环卷积中哪些序列值等于线性卷积得到的值，而哪些序列值不等于线性卷积的值。x₁[n]和x₂[n]的线性卷积是一个长度为（N₁+N₂-1）的有限长序列，如图2.6.3（c）所示。为了确定N₁点循环卷积，利用式（2.6.7）和式（2.6.8）则有

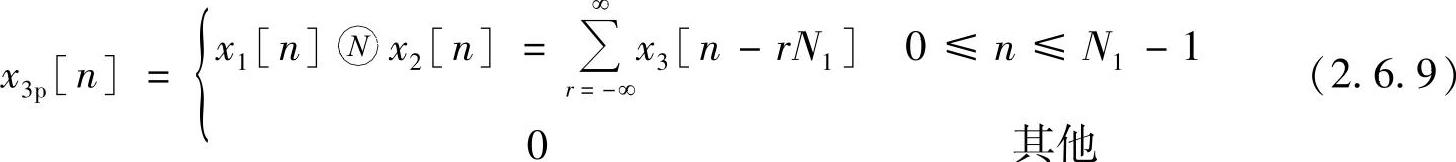
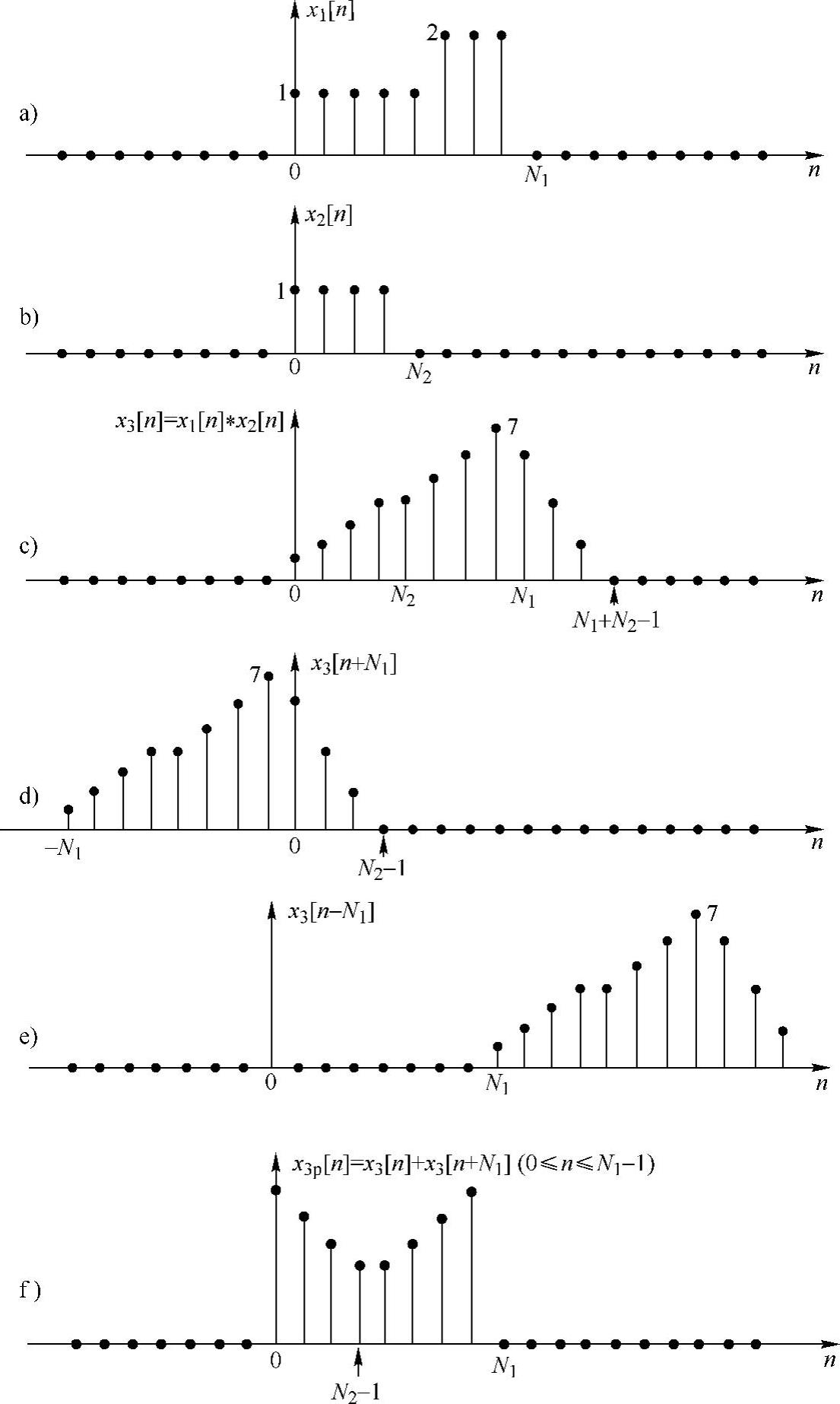
图2.6.3 两个有限长序列的循环卷积可以看做线性卷积加上混叠

图2.6.3c表示式（2.6.9）中当r=0时的项，图2.6.3d、e分别表示r=-1和r=1的项。从图2.6.3可以清楚地看到，在区间0≤n≤N₁-1上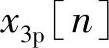，只受x₃[n]和x₃[n+N₁]的影响。

总之，只要当N₂＜N₁时，只有项x₃[n+N₁]在区间产生混叠。更明确地讲，当这些项加在一起时，x₃[n+N₁]的最后（N₂-1）个点，即从n=0到n=N₂-2，将加在x₃[n]的最初（N₂-1）个点上，而x₃[n]的最后（N₂-1）个点，即从n=N₁到n=N₁+N₂-2，将被丢掉。这样截取0≤n≤N₁-1的部分就形成了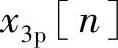。由于x₃[n+N₁]的（N₂-1）个点的值等于x₃[n]的最后（N₂-1）个点的值，所以可以用另一种观点来看待形成循环卷积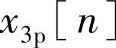的过程，即通过线性卷积加上x₃[n]的从n=N₁到n=N₁+N₂-2的（N₂-1）个值加在x₃[n]的最初（N₂-1）个值上的混叠来形成。图2.6.4说明当N₁=8和N₂=4时的这一过程。图2.6.4a表示线性卷积x₃[n]，对于n≥N₁的点用空心圆符号来标记。注意对于n≥N₁只有（N₂-1）个点非零。图2.6.4b表示利用“x₃[n]的自身卷绕”来形成x_3p[n]。最初的（N₂-1）点有时间混叠掺入，而其余的从n=N₂-1到n=N₁-1个点（即最后N₁-N₂+1点）不受破坏，也就是等于用线性卷积所得到的那些点的值。

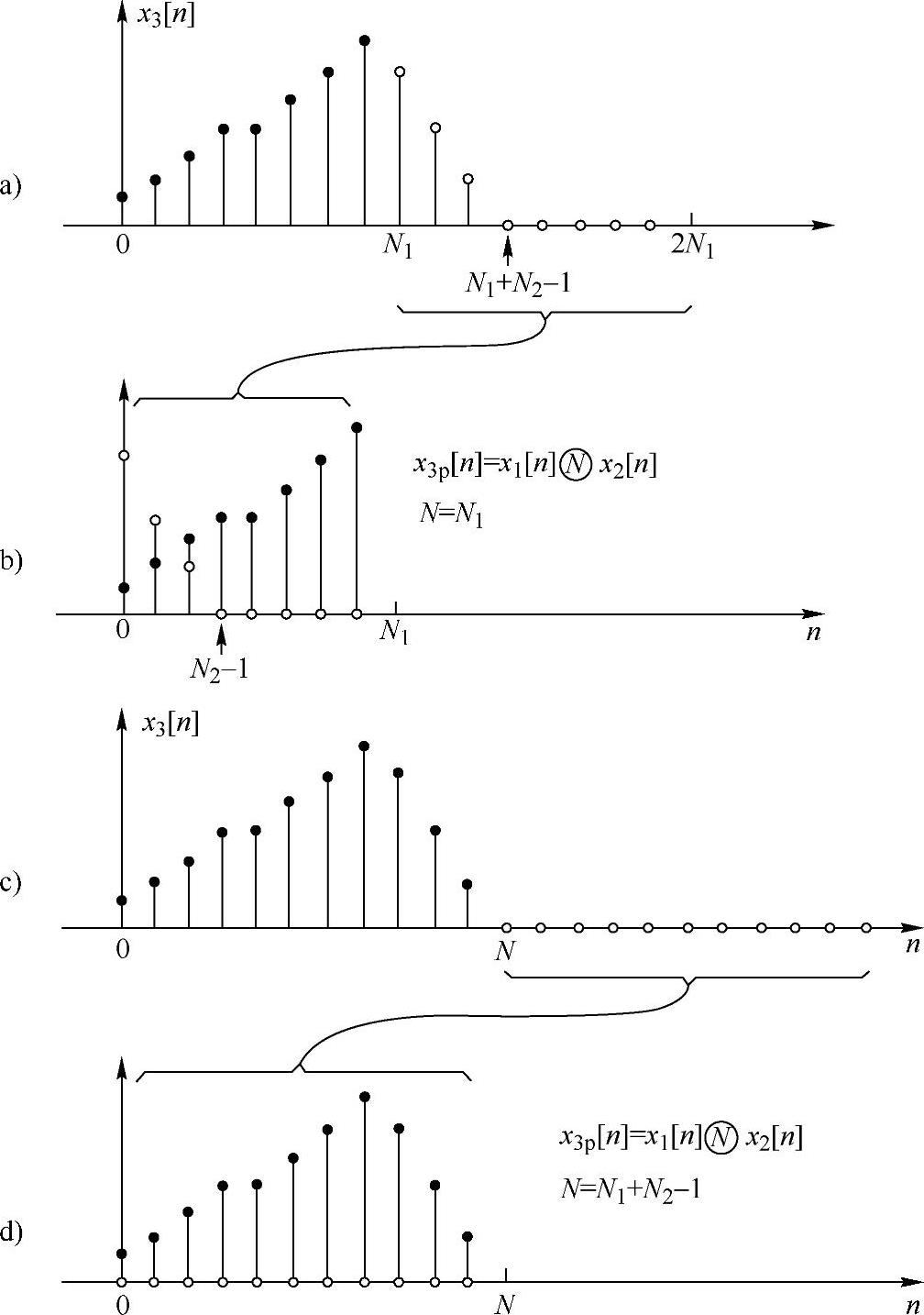
图2.6.4 产生卷绕的过程

从以上讨论可知，如果循环卷积的长度相对于序列x₁[n]和x₂[n]的长度足够长的话，就可以避免非零值的混叠，在这种情况下，循环卷积就等于线性卷积。具体讲，若对于刚才考虑的情况，x₃[n]以N≥N₁+N₂-1的周期重复，则不会产生非零的重叠。图2.6c、d说明了这种情况，此时N₁=8，N₂=4，且N=11。