循环卷积定理及应用实例

设有限长序列x₁[n]和x₂[n]的N点离散傅里叶变换分别为X₁[k]和X₂[k]，且设X₃[k]=X₁[k]X₂[k]，则X₃[k]的离散傅里叶反变换x₃[n]为

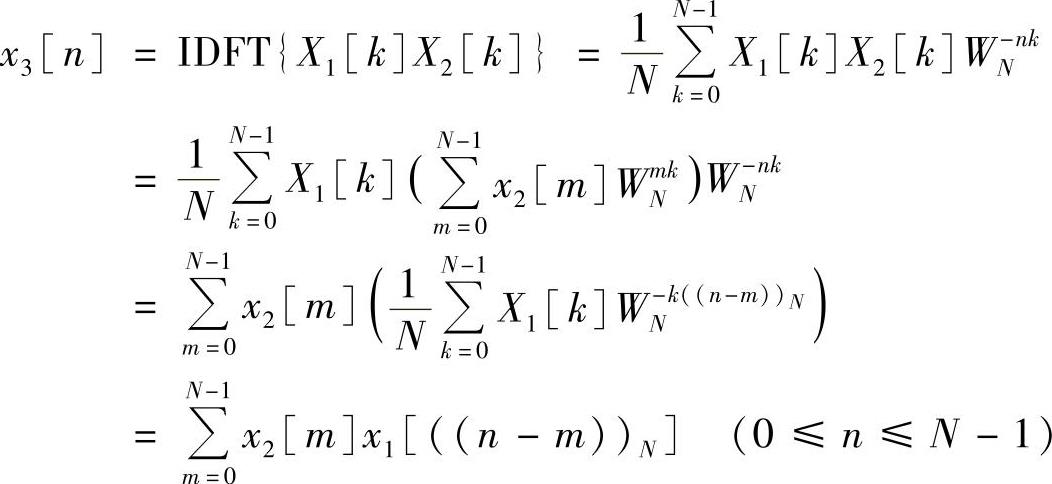
即

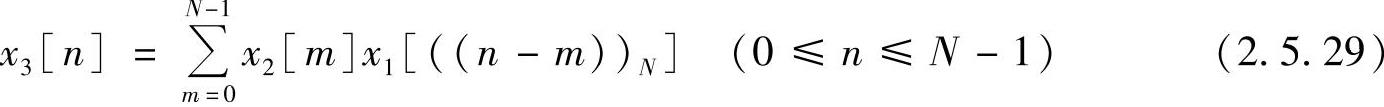
式（2.5.29）也可写成

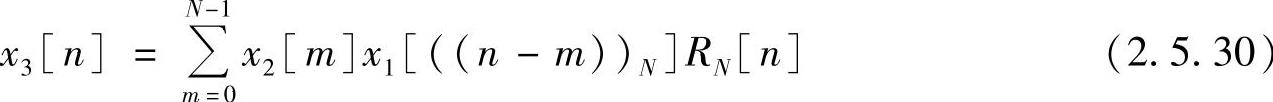
把式（2.5.29）的运算称为x₁[n]和x₂[n]的循环卷积。后续内容用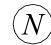表示N点循环卷积。于是式（2.5.29）可以记为

上述说明，两个序列的离散傅里叶变换的积的离散傅里叶反变换是两个序列的循环卷积，这就是循环卷积定理。实际上，循环卷积是两个序列周期延拓后的一个周期上的线性卷积。下面举例说明循环卷积的运算过程。

【例2.5.2】 设x₂[n]是一个长度为5的有限长序列，其波形如图2.5.3a所示，而x₁[n]=δ[n-1]，求x₁[n]和x₂[n]的5点循环卷积。

解 设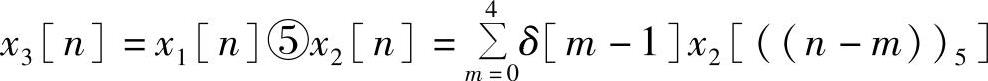 （0≤n≤4），则其运算过程如图2.5.3b～f所示。

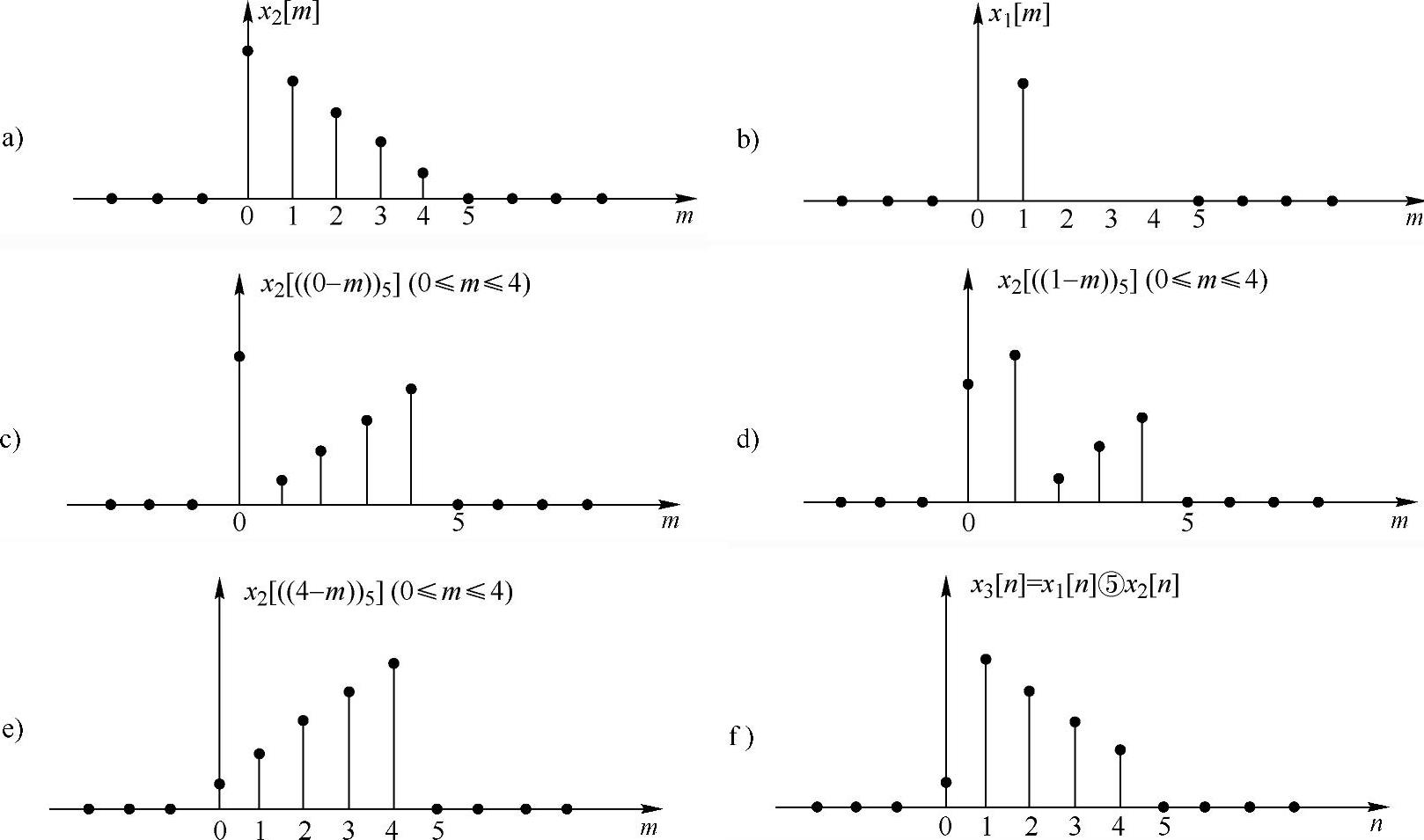
图2.5.3 有限长序列x₂[n]和一个延迟的单位抽样 序列x₁[n]=δ[n-1]的循环卷积

【例2.5.3】 求两个矩形序列x₁[n]=x₂[n]=R₆[n]（见图2.5.4a、b）的6点和12点循环卷积。(www.xing528.com)

解 1）6点循环卷积。

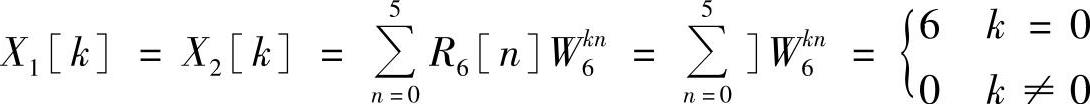
应用循环卷积定理，将X₁[k]和X₂[k]相乘，得

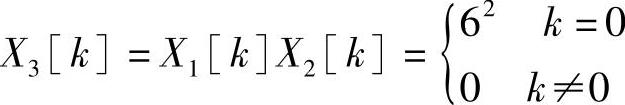
于是

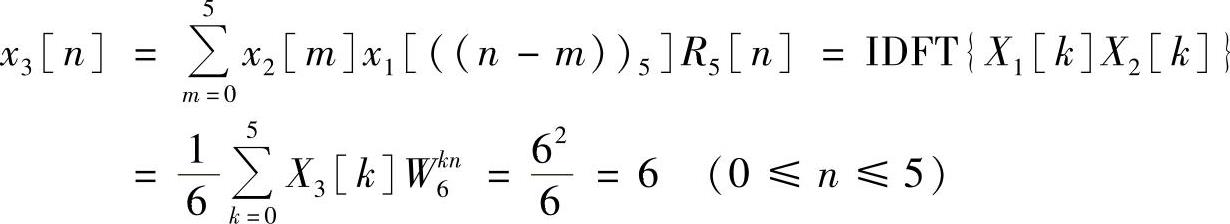
其波形如图2.5.4c所示。

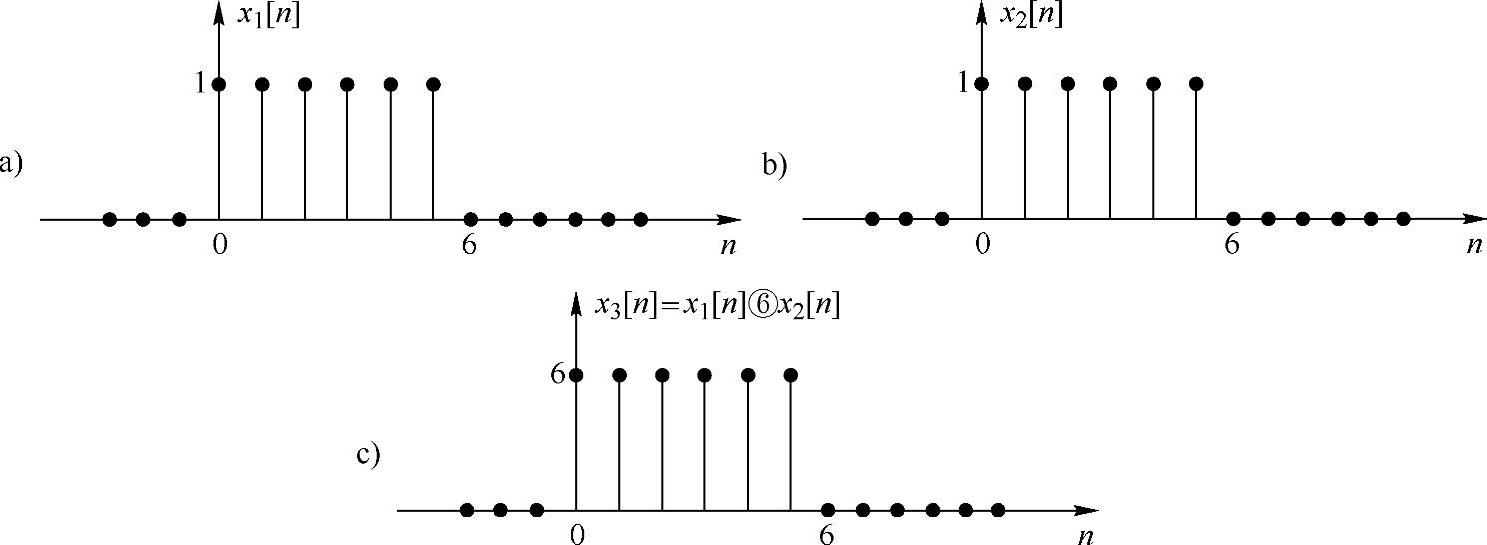
图2.5.4 两个长度为6的矩形序列的6点循环卷积

2）12点循环卷积，给x₁[n]和x₂[n]增补6个0。

从图2.5.5可以看出，两个长度为6的有限长序列的12点循环卷积等于它们的线性卷积。在下一节，将详细讨论这个重要结论。

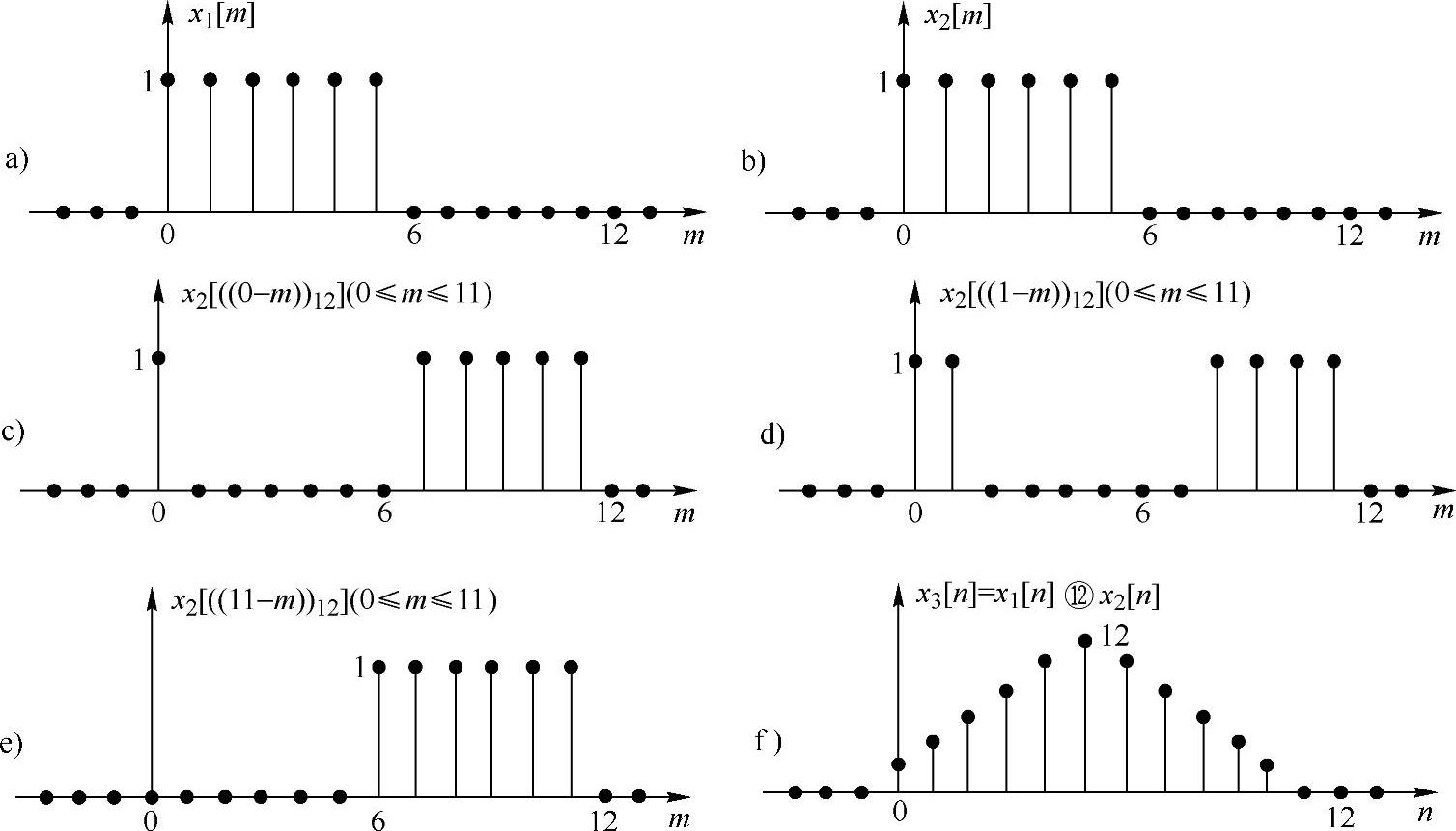
图2.5.5 两个长度为6的矩形序列的12点循环卷积