离散傅里叶变换及其应用

离散傅里叶变换（DFT）是连续傅里叶变换在时域和频域上都离散的形式，将时域信号的采样变换为在离散时间傅里叶变换（DTFT）频域的采样。在形式上，变换两端（时域和频域上）的序列是有限长的，而实际上这两组序列都应当被认为是离散周期信号的主值序列。即使对有限长的离散信号作离散傅里叶变换，也应当将其看做经过周期延拓成为周期信号再作变换。在实际应用中通常采用快速傅里叶变换以高效计算离散傅里叶变换。

本节用公式来描述上一节末所建议的观点。首先，来研究一个长度为N的有限长序列x[n]，在0≤n≤N-1之外x[n]=0。把它与一个周期序列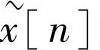连续起来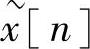，由下式给出，即

有限长序列x[n]可以通过式（2.3.3）由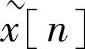来恢复，即

由上节可知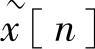，的傅里叶级数的系数是x[n]的傅里叶变换的采样（频率间隔为2π/N）。因为x[n]的长度为N，所以对于不同的r值，在x[n-rN]各项之间没有重叠。这样，式（2.4.1）可以写成另一种形式

为了方便起见，用符号（（n））N表示（n以N为模）。利用这种符号，式（2.4.3）可以表示为

只有当x[n]的长度小于或等于N时，式（2.4.4）与式（2.4.1）才等价。有限长序列x[n]是由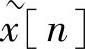取出一个周期得到的，见式（2.4.2）。

对式（2.4.3）的描述，可以想象成把有限长序列x[n]缠绕在一个周长等于序列长度的圆柱体上。如果重复地转动圆柱体的圆周，就会看到有限长序列周期地重复着。利用这种解释，用一个周期序列来表示有限长序列就相当于把该序列围绕着这种圆柱体缠绕。

周期序列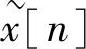的离散傅里叶级数的系数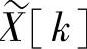本身是一个周期为N的周期序列。为了保持时域和频域之间的对偶性，将把与有限长序列相联系的傅里叶系数选为与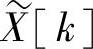的一个周期相对应的有限长序列。这个有限长序列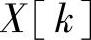称为离散傅里叶变换。因此，离散傅里叶变换X[k]和离散傅里叶级数的系数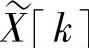的关系为

和

重写式（2.2.62）为

并考虑式（2.4.2）和式（2.4.5）可得

如果规定只讨论一个周期，就可以写出以下一对变换，即

这一变换对称为离散傅里叶变换对，式（2.4.9）称为正变换，式（2.4.10）称为逆变换。

通常将离散傅里叶正变换和逆变换写为

式中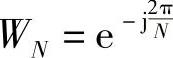，。(www.xing528.com)

从离散傅里叶的变换对的导出过程可以看出，实质上X[k]和x[n]都是周期性的，只不过讨论时仅取其周期序列的一个周期，因而把式（2.4.11）所表示的取值区间0≤k≤N-1和0≤n≤N-1定为主值区间，而主值区间内的一个周期序列值X[k]和x[n]定义为主值序列。

离散傅里叶变换式（2.4.11）是一线性方程组，它由N个x[n]值变换（映射）成另外N个值X[k]。可以用矩阵方程来表示。设x为由x[n]（0≤n≤N-1）构成的列矩阵，X为由X[k]（0≤k≤N-1）构成的列矩阵，即

则有

X=W_Nx （2.4.12）

式中，W_N为N×N方阵，其中第i行和第j列的元素为W^ij_N。例如对于N=5点的离散傅里叶变换，就可以表示成

由W_N的对称性可知

W_N=W^T_N （2.4.14）

而且有

X=W^T_Nx （2.4.15）

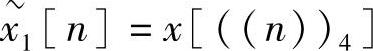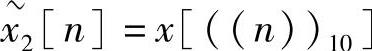【例2.4.1】 设有限长序列x[n]={1，2，3，4，5，6，7}，分别求和各序列。

解 1）求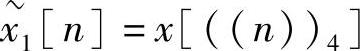的一个周期序列。按式（2.4.1）有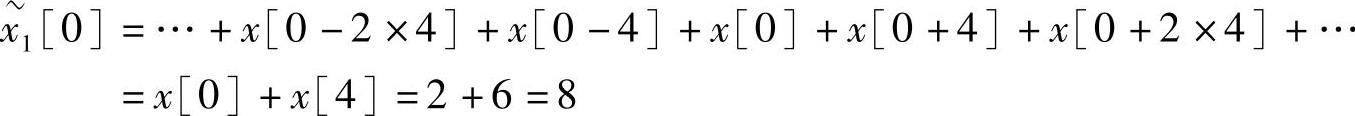同理可以求得

所以要求的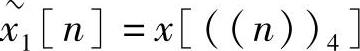的一个周期序列值为

2）求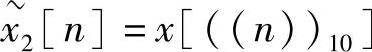的一个周期序列值。由于序列长度M=7，要求是以N=10点为周期进行延拓，因而不足部分补零。其中

所以要求的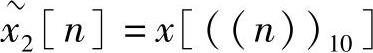的一个周期序列值为