如何采样傅里叶变换？

在这一节中将讨论非周期序列和周期序列之间更一般的关系，前者具有傅里叶变换X（e^jω）的形式，后者的傅里叶级数系数对应于X（e^jω）在频域上等间隔采样。我们将会发现，在下一节讨论的离散傅里叶变换（Discrete Fourier Transform，DFT）及其性质时，这一关系是非常重要的。

一个非周期序列x[n]，其傅里叶变换为X（e^jω），并假设序列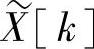是通过对X（e^jω）在ω_k=2πk/N频率处采样得到的，即

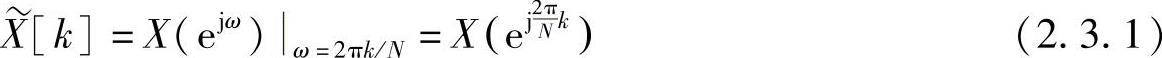
因为傅里叶变换是ω的周期函数，周期为2π，所以得出的序列是k的周期函数，周期为N。同样，因为傅里叶变换等于z变换在单位圆上的值，所以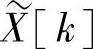也可以由在单位圆的N个等间隔的点上对X（z）采样得到。这样有

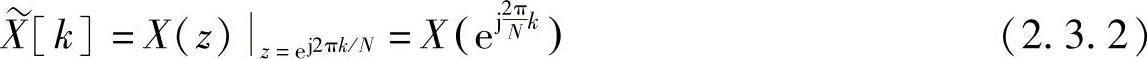
在图2.3.1中绘出了N=8的这些采样点。由于N个点是从0°开始等间隔分布的，所以从图中可以清楚地看出，样本序列是周期的，因此在区间0≤k≤N-1之外随着k的变化会重复同样的序列。(www.xing528.com)

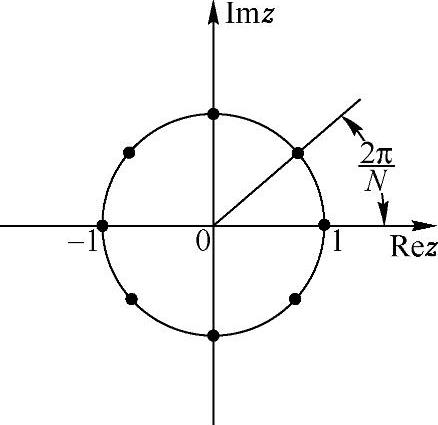
图2.3.1 在单位圆上对X（z）进行采样的点，从而得到周期序列X[k]

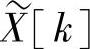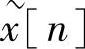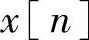可以看到，样本序列是周期序列，周期为N，它可以是一个序列的离散傅里叶级数的系数序列。所以，可以把一个非周期序列的傅里叶变换的采样看做是通过将周期重复而得到的一个周期序列的离散傅里叶级数的系数。如果x[n]为有限长，并且取其傅里叶变换足够多的等间隔采样（特别是，个数大于或等于x[n]的长度），则傅里叶变换是可以由这些采样值来恢复的。同样，x[n]可以由如下关系来恢复，即

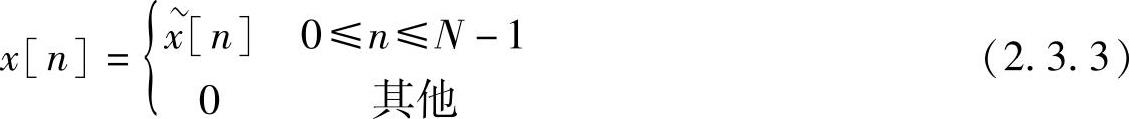
可以推导出X（e^jω）和采样X[k]之间的直接关系，即对于X（e^jω）的内插公式（见习题2.25）。然而，以上讨论的基本点是，如果x[n]是有限长，要表示或恢复x[n]就没有必要知道在所有频率处的X（e^jω）值。若给出一个有限长序列x[n]，就能按式（2.2.57）形成一个周期序列，也就能用傅里叶级数来表示。另外，若给出傅里叶系数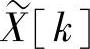，就可以求出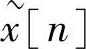，然后用式（2.3.3）得到x[n]。当利用傅里叶级数以这种方式来表示有限长序列时，就将它称为离散傅里叶变换（DFT）。在推导、讨论和应用离散傅里叶变换时，始终应记住十分重要的一点：通过傅里叶变换的采样值来表示，实际上是利用一个周期序列来表示有限长序列，该周期序列的一个周期正是要表示的有限长序列。