周期性序列的傅里叶变换

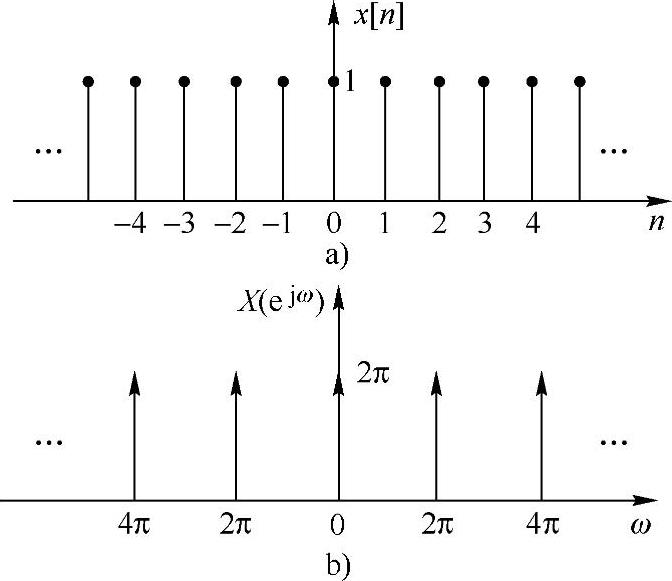
图2.2.5 x[n]=1的序列及其傅里叶变换

周期性序列既不是绝对可和也不是能量有限的二次方可和序列，它的z变换不存在。但引入冲激函数δ（ω），它的傅里叶变换就可以存在，这样可以精确地描述周期性信号的频谱特性，因而在理论和实践中得以广泛的应用。

首先考察序列x[n]=1（-∞＜n＜∞）的傅里叶变换。如图2.2.5a所示，实际上它是周期N=1的周期性序列，即

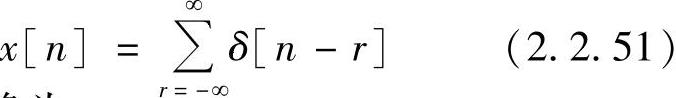
它的傅里叶变换为

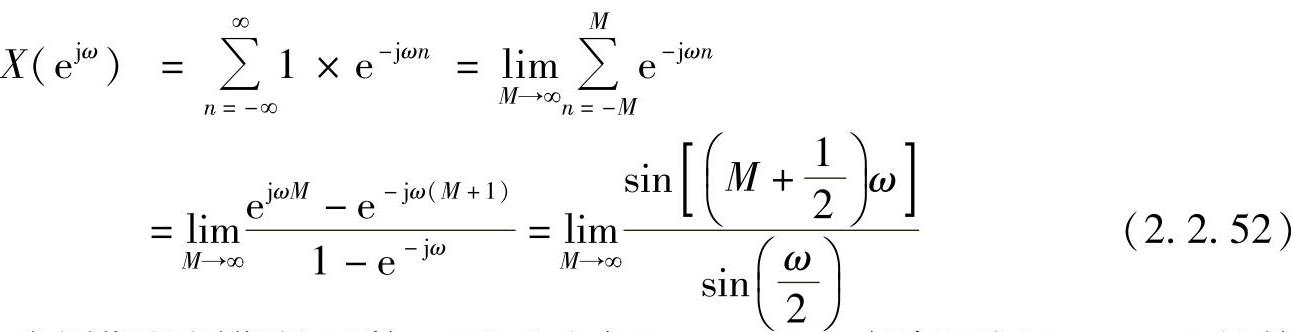
由于X（e^jω）是以ω=2π为周期的周期性函数，因而对式（2.2.52），考察区间（-π，π）的特性，有

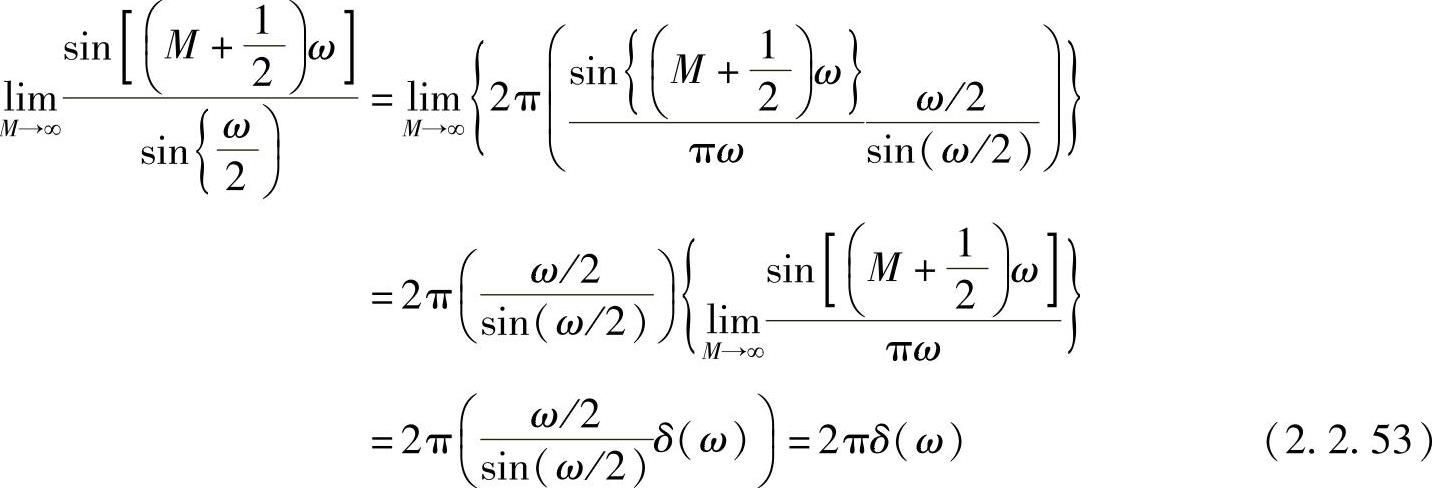
考虑到X（e^jω）的周期性，因此有

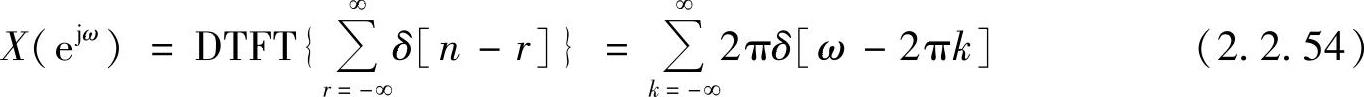
所以常数系列的傅里叶变换是一系列冲激函数，如图2.2.5b所示。

利用傅里叶变换的频域移位性可得

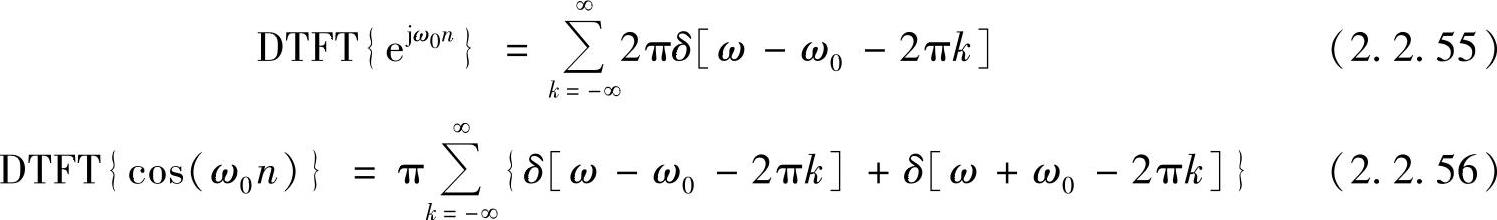
对于一般的周期序列x[n]，可以写成

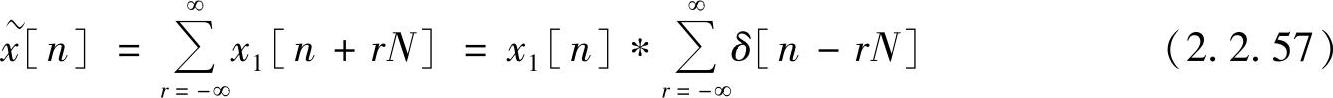
式中，x₁[n]及其傅里叶变换X₁（e^jω）如图2.2.6a所示。而周期性单位抽样序列的傅里叶变换可以用下述方法求得（见图2.2.6b）(https://www.xing528.com)

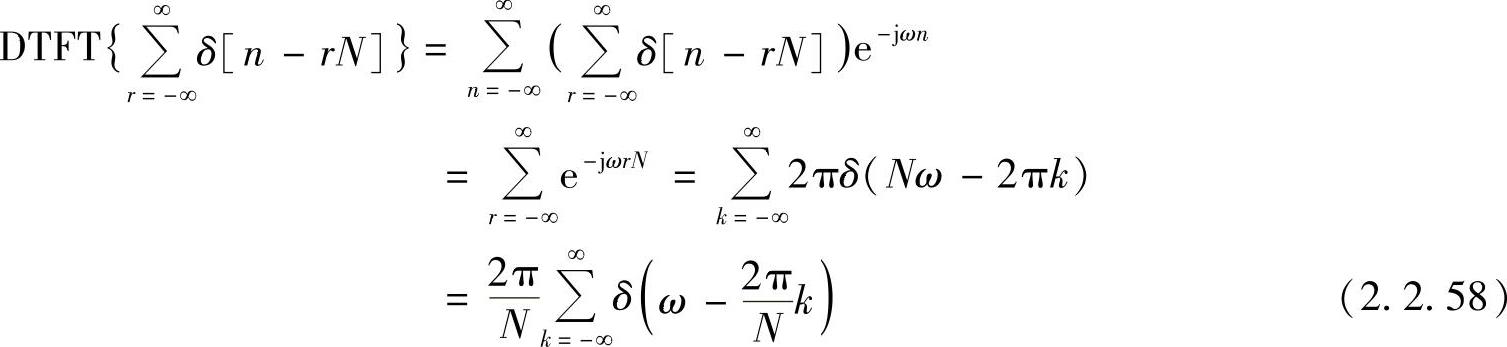
根据离散时间傅里叶变换的时域卷积定理，周期序列x[n]的傅里叶变换为（见图2.2.6c）

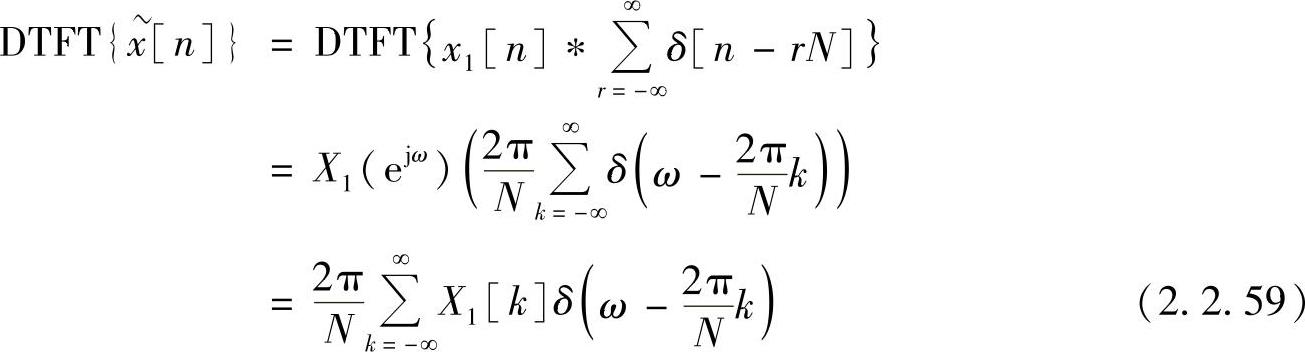
式（2.2.59）表明，周期性序列的傅里叶变换相当于周期性序列中一个周期内序列的傅里叶变换在频域中的抽样。图2.2.6描述了周期性序列及其傅里叶变换。式（2.2.59）中

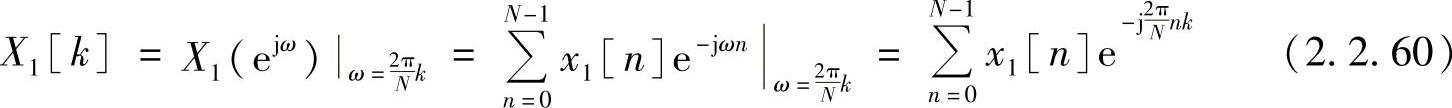
式（2.2.59）的傅里叶逆变换为

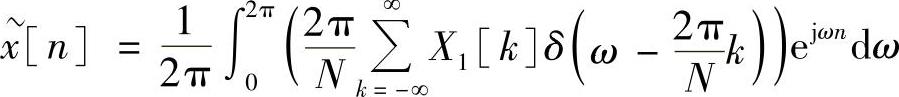
为讨论方便，上式求逆变换的区间取为（0，2π）。由于被积函数是以2π为周期的周期函数，因而在一个区间内，k的取值范围为0≤k≤N-1，这样上式可以改写为

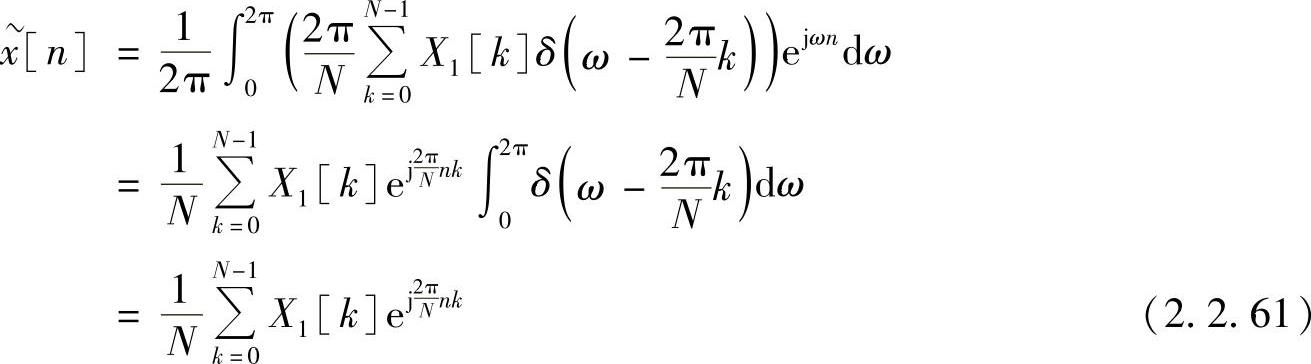
式中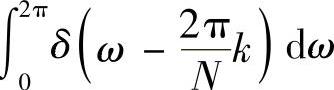，对给定的k，积分值等于1。

式（2.2.61）就是周期性序列的傅里叶级数展开，它表明周期性序列由N个谐波分量组成，谐波分量的频率为2πk/N（k=0，1，2，…，N-1），各次谐波分量的幅度为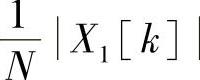，X₁[k]由式（2.2.60）所决定，它是傅里叶级数展开的系数。式（2.2.60）和式（2.2.61）构成一对傅里叶级数（DFS）的关系，统一表示成

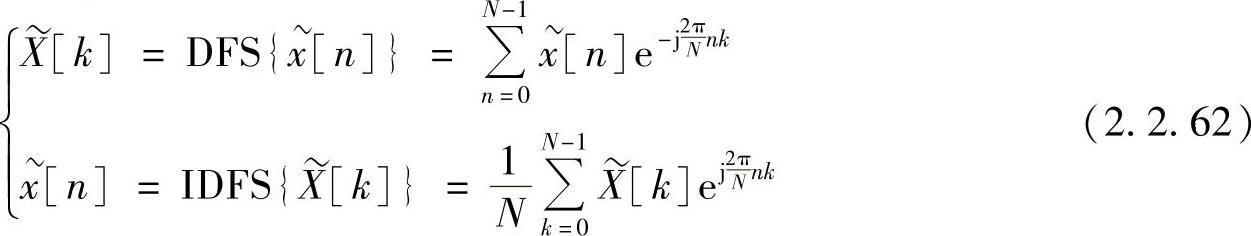
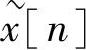和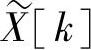都是以N为周期的周期性序列。

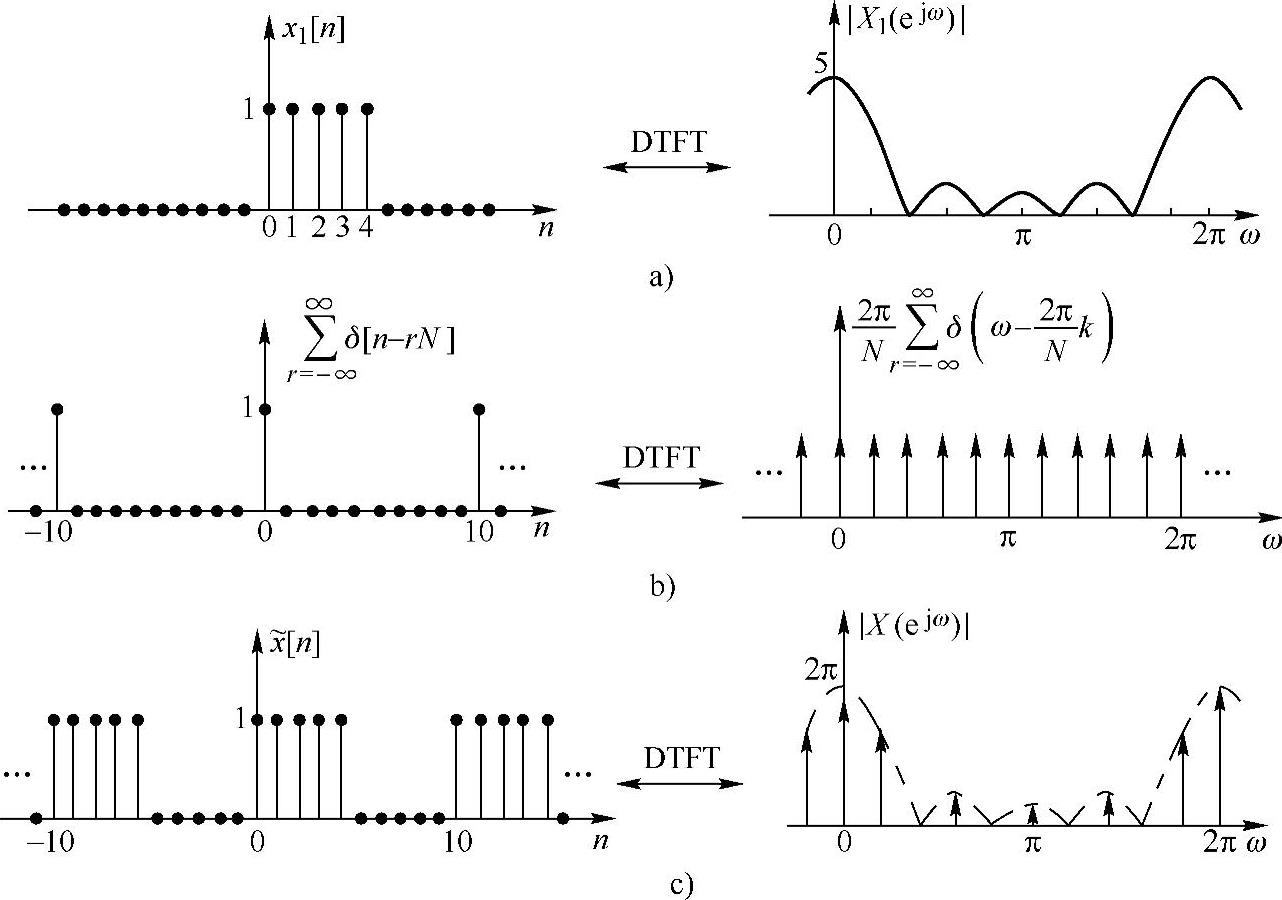
图2.2.6 周期性序列的傅里叶变换