离散时间傅里叶变换的对称性优化为：离散时间傅里叶变换中的对称性

傅里叶变换有许多对称性质，这些对称性质是很有用的。下面先介绍共轭对称序列与共轭反对称序列及它们的性质。

设序列x[n]是复序列，则它们可以分解为

x[n]=x_e[n]+x_o[n] （2.2.31）

式中，x_e[n]称为共轭对称分量，它满足

x_e[n]=x^∗_e[-n] （2.2.32）

能满足式（2.2.32）特性的序列称为共轭对称序列。

x_o[n]称为共轭反对称分量，它满足

x_o[n]=-x^∗_o[-n] （2.2.33）

同样，能满足式（2.2.33）特性的序列称为共轭反对称序列。

对式（2.2.31）两边取共轭再反转，同时利用式（2.2.32）和式（2.2.33）的特性，有

x^∗[-n]=x^∗_e[-n]+x^∗_o[-n]

=x^∗_e[n]-x^∗_o[n] （2.2.34）

联立式（2.2.31）和式（2.2.34）可得到共轭对称分量和共轭反对称分量分别为

【例2.2.3】 对复指数序列x₁[n]=e^jωn和x₂[n]=je^jωn分析其对称性。

解 1）对序列x₁[n]=e^jωn分解，得

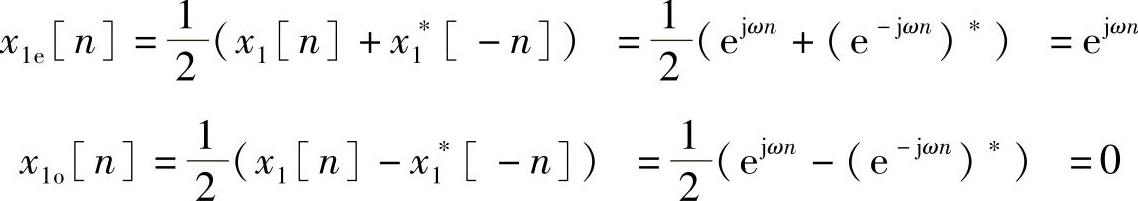
这说明序列e^jωn本身是共轭对称序列，它具有共轭对称性，即x₁[n]=x^∗₁[-n]。

2）对序列x₂[n]=je^jωn分解，得

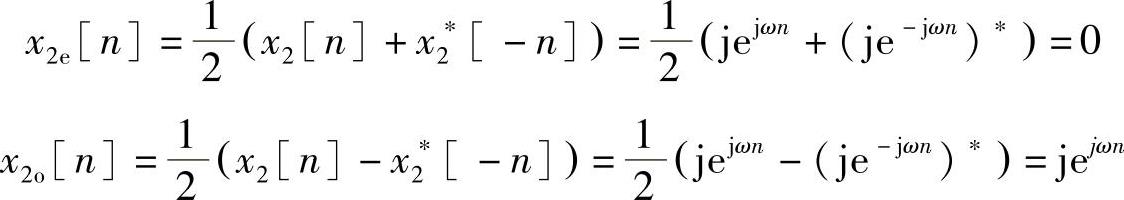
可见序列je^jωn是共轭反对称序列，它具有共轭反对称性，即x₂[n]=-x^∗₂[-n]。

3）同时复指数序列x₁[n]=e^jωn和x₂[n]=je^jωn可以展开成实部与虚部，即

x₁[n]=e^jωn=cosωn+jsinωn

x₂[n]=je^jωn=-sinωn+jcosωn

从例2.2.3可以推论得出：

1）共轭对称序列乘以j得到的序列是共轭反对称序列；而共轭反对称序列乘以j得到的序列是共轭对称序列。

2）共轭对称序列的实部是n的偶函数，虚部是n的奇函数；共轭反对称序列的实部是n的奇函数，虚部是n的偶函数。

对于离散时间傅里叶变换X（e^jω）可以有同样的分解，即

X（e^jω）=DTFT{x[n]}=X_e（e^jω）+X_o（e^jω） （2.2.37）

式中，共轭对称分量X_e（e^jω）满足

X_e（e^jω）=X^∗_e（e^-jω） （2.2.38）

共轭反对称分量X_o（e^jω）满足

X_o（e^jω）=-X^∗_o（e^-jω） （2.2.39）

傅里叶变换的对称性描述如下：

由共轭序列和序列反转性得出

DTFT{x^∗[-n]}=X^∗（e^jω） （2.2.40）

因此有(www.xing528.com)

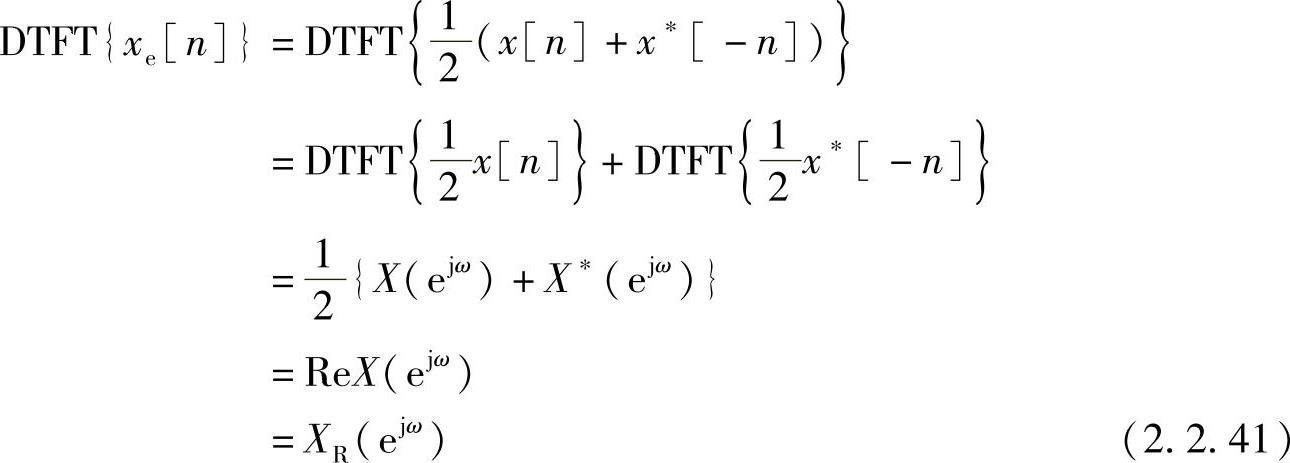
上式说明序列的共轭对称分量的傅里叶变换是原序列傅里叶变换的实部。

同理有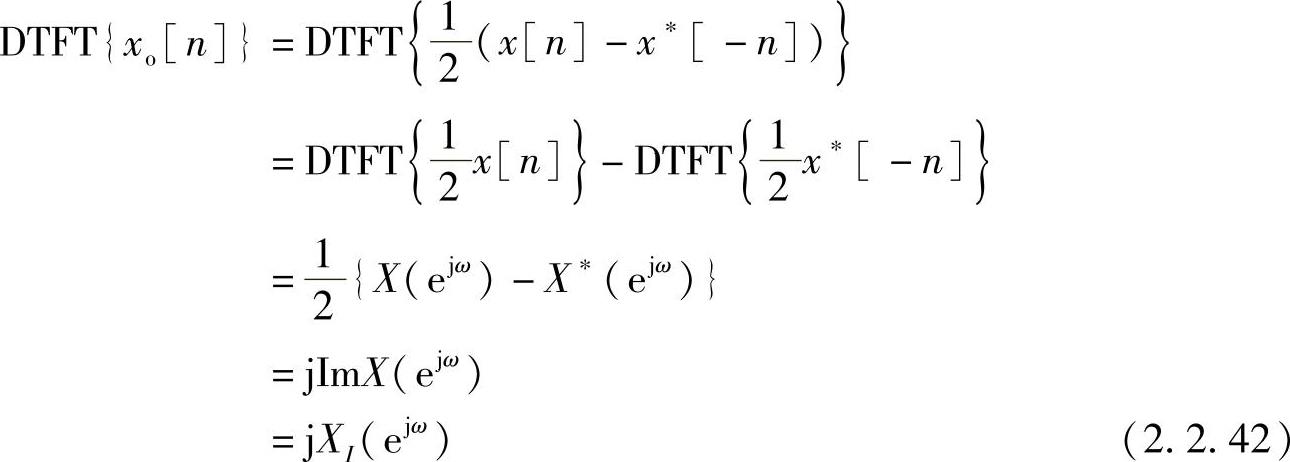

即序列的共轭反对称分量的傅里叶变换是原序列傅里叶变换的虚部（包含j）。

复序列可表示为

x[n]=x_r[n]+jx_i[n] （2.2.43）

其实部x_r[n]的傅里叶变换为

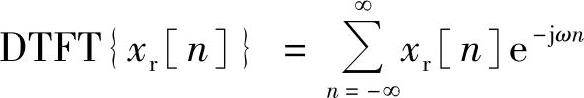
将上式右边的ω加负号，再取共轭得

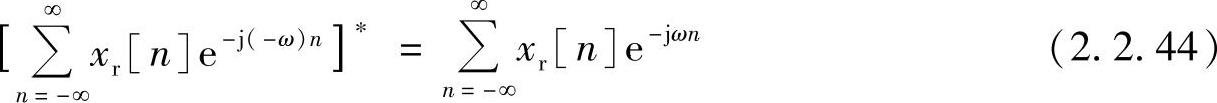
式（2.2.44）表明实序列的傅里叶变换具有共轭对称性质，用X_e（e^jω）表示。

同理有

将上式右边的ω加负号，再取共轭得

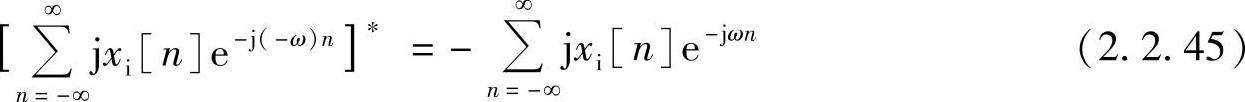
式（2.2.45）表明j乘以实序列x_i[n]的傅里叶变换具有共轭反对称性质，用X_o（e^jω）表示。

这样，像时域复序列分解一样

X（e^jω）=X_e（e^jω）+X_o（e^jω）

=DTFT{x_r[n]}+DTFT{jx_i[n]} （2.2.46）

式中，。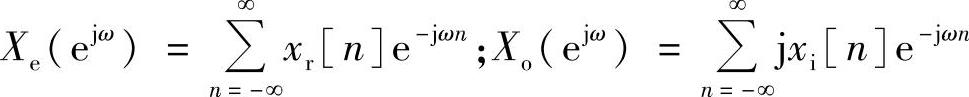

作为上列离散时间傅里叶变换对称性的一个重要特殊情况，即序列是实序列的情况，可以得出以下结论：

实序列的傅里叶变换具有共轭对称性，即

X（e^jω）=X^∗（e^-jω） （2.2.47）

由此得出

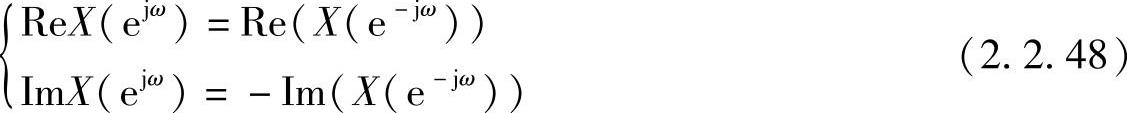
所以实序列的傅里叶变换的实部是ω的偶函数，而虚部是ω的奇函数。

X（e^jω）的幅频特性与相频特性可表示为

X（e^jω）=|X（e^jω）|ejarg[X（ejω）]

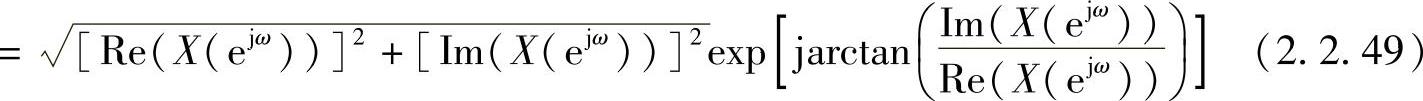
则有

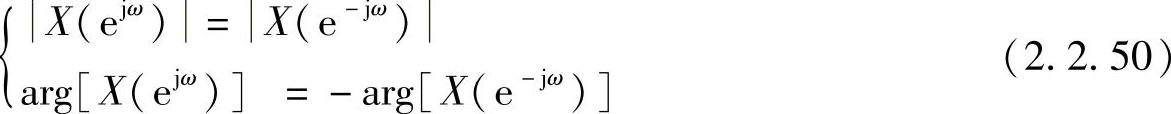
所以实序列的幅频特性是ω的偶函数，相频特性是ω的奇函数。

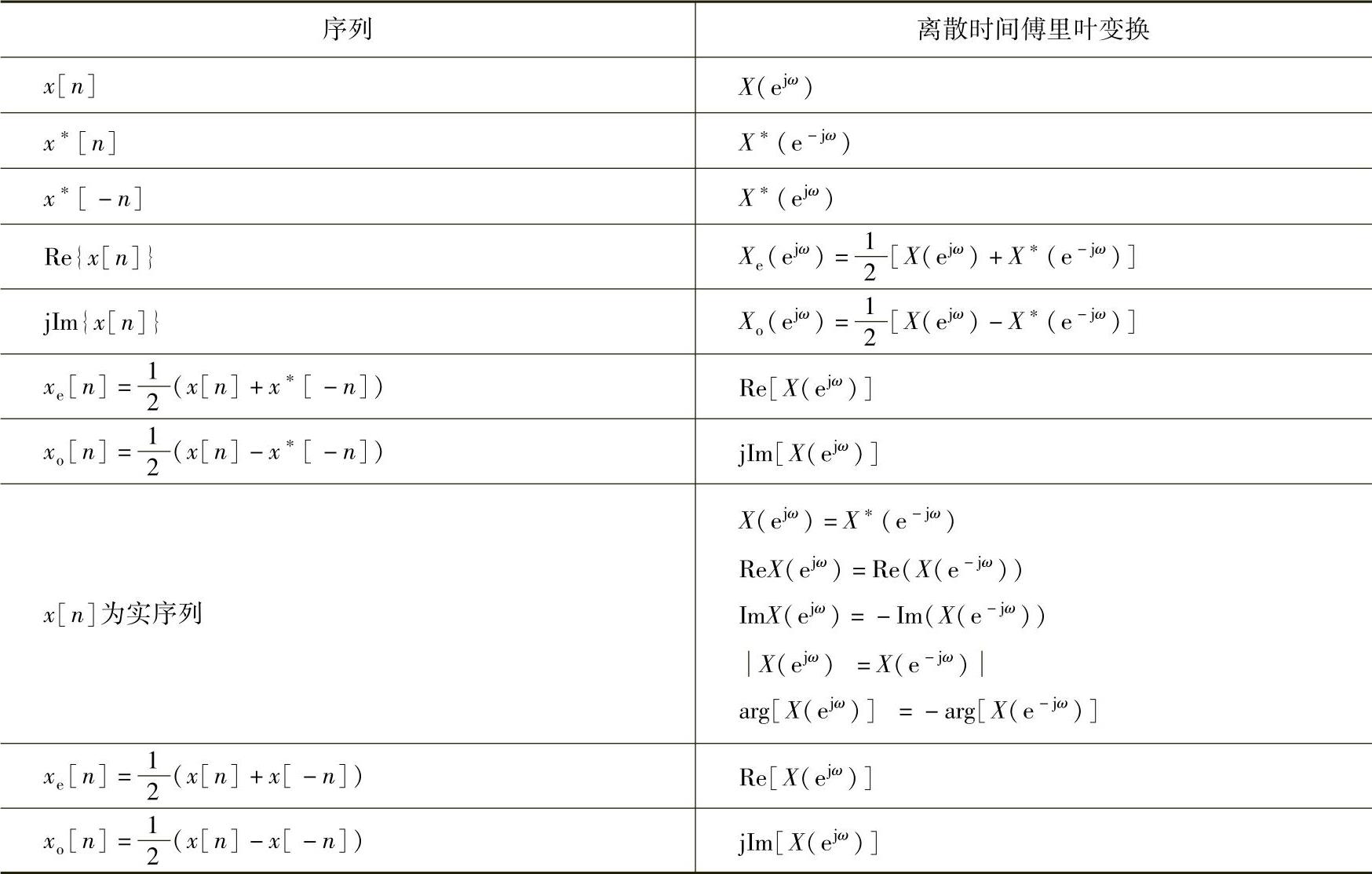
离散时间傅里叶变换的对称性见表2.2.2。

表2.2.2 离散时间傅里叶变换的对称性