【摘要】:离散时间傅里叶变换是离散时间信号频谱分析和离散时间系统频率响应求解的基础。图2.2.4 指数序列x[n]波形那么则方法二:设x[n]的波形与图2.2.3类似,则u[n]的奇部为那么则3.累加器的离散时间傅里叶变换累加器是数字电路中的重要系统,累加器的输入输出满足如下关系从式可以求出累加器系统的单位抽样响应h[n]为从式可知累加器系统的单位抽样响应是单位阶跃序列,所以y[n]=h[n]x[n]=u[n]x[n] 则y的离散时间傅里叶变换为
阶跃信号是某些物理现象从一个状态瞬间变化到另一个状态的理想化数学抽象,是信号与线性系统分析中不可缺少的典型基本信号模型之一。其中单位阶跃序列u[n]是离散时间信号与线性系统分析的典型基本信号模型。离散时间傅里叶变换是离散时间信号频谱分析和离散时间系统频率响应求解的基础。
1.奇偶分解
u[n]=ue[n]+uo[n] (2.2.13)
其中偶部
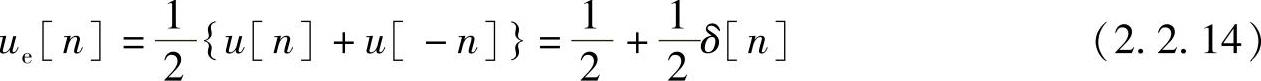
奇部
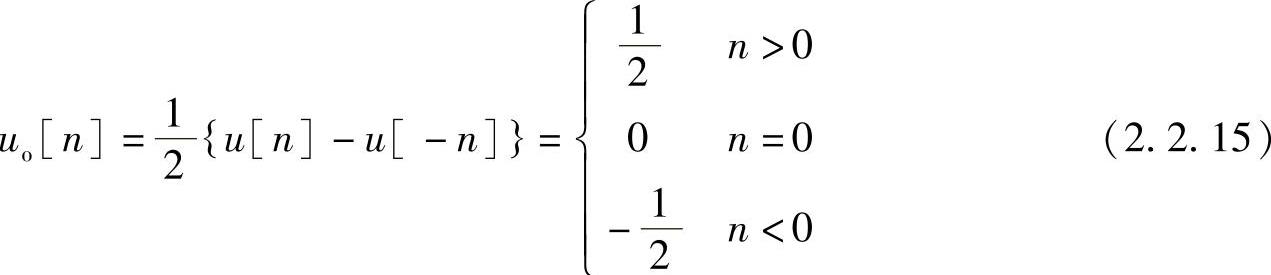
偶部与奇部序列如图2.2.3所示
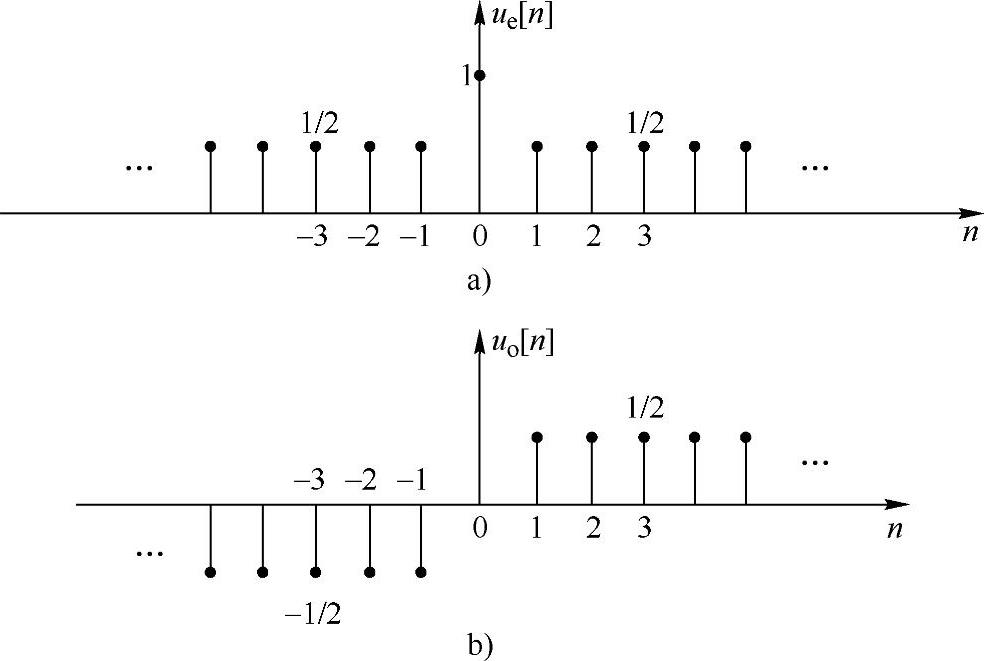
图2.2.3 单位阶跃序列的奇偶分解
a)偶部 b)奇部
2.u[n]的离散时间傅里叶变换
分别求偶部和奇部的傅里叶变换,则ue[n]的傅里叶变换为

关于奇部uo[n]可以看做指数序列求极限,可用如下两种方法求解。
方法一:
设
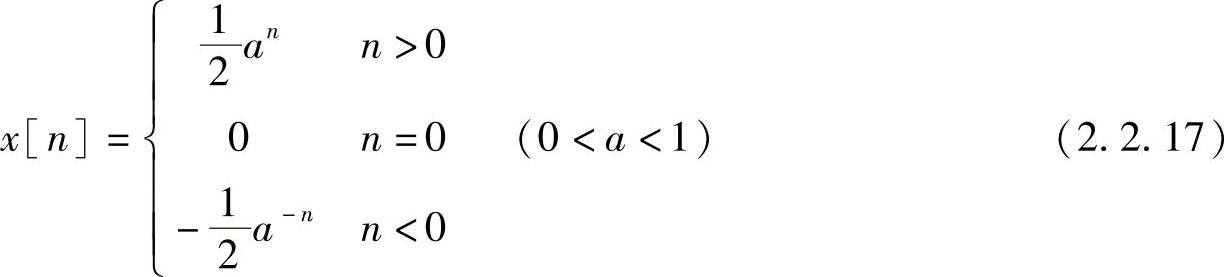
x[n]的波形如图2.2.4所示。
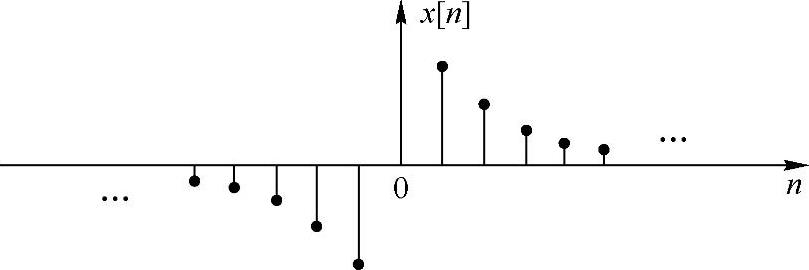
图2.2.4 指数序列x[n]波形
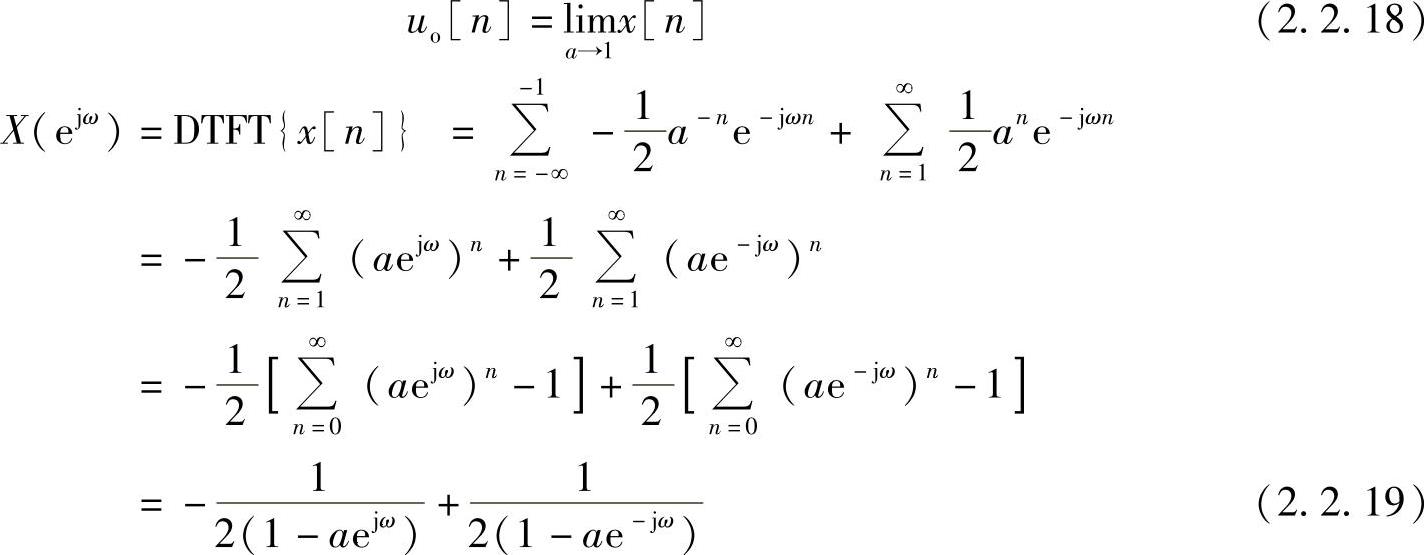
那么(https://www.xing528.com)
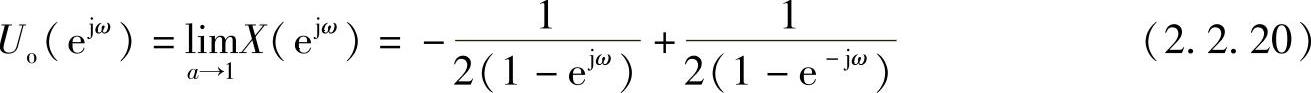
则
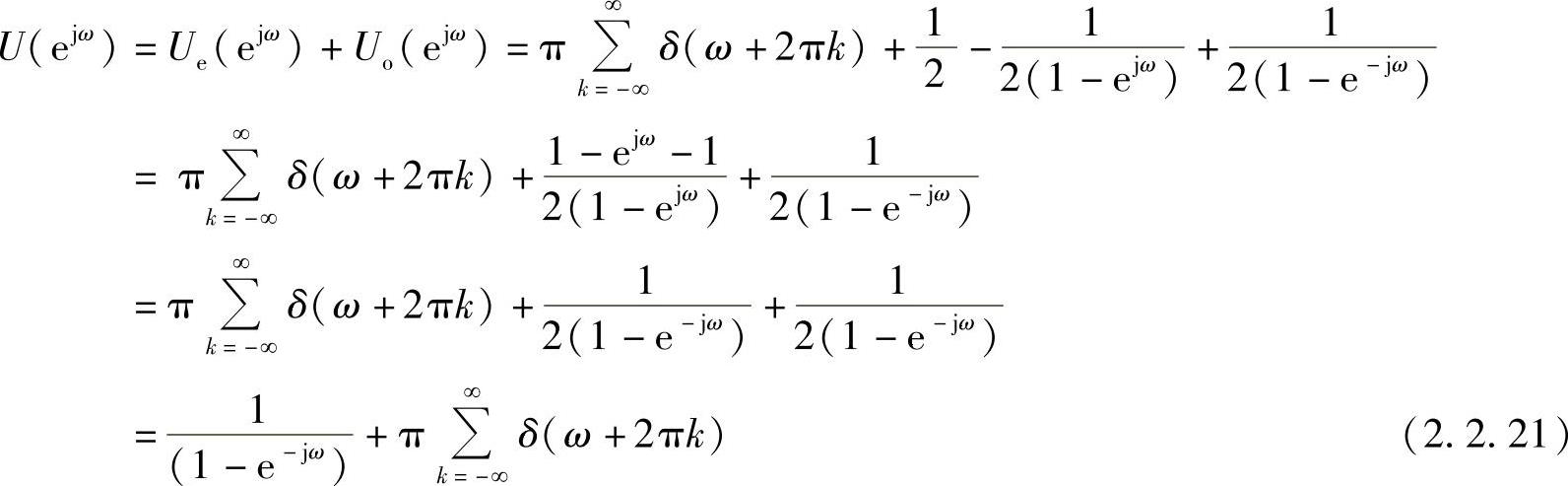
方法二:
设

x[n]的波形与图2.2.3类似,则u[n]的奇部为
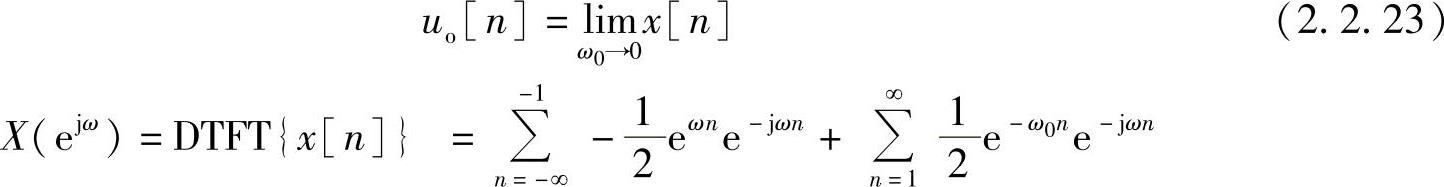
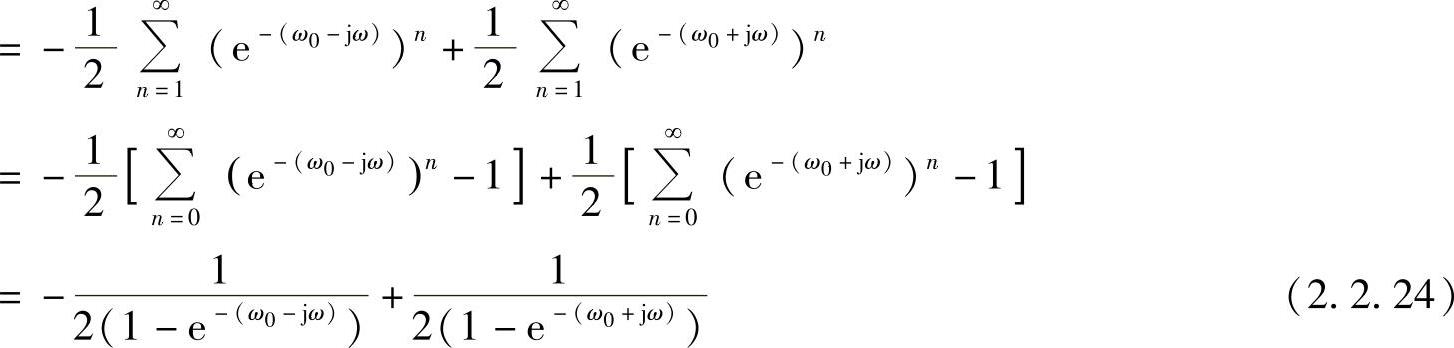
那么
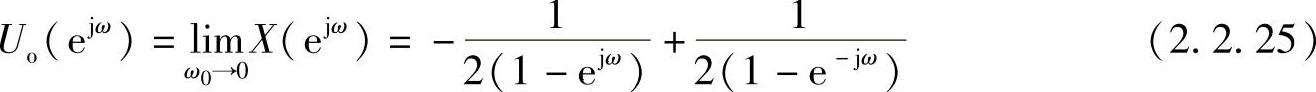
则
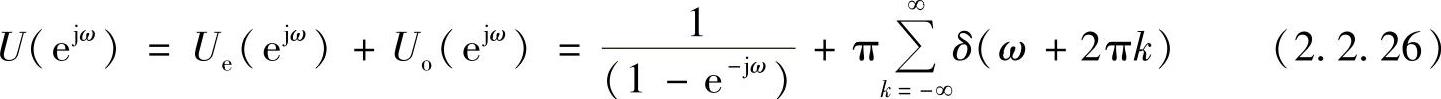
3.累加器的离散时间傅里叶变换
累加器是数字电路中的重要系统,累加器的输入输出满足如下关系

从式(2.2.27)可以求出累加器系统的单位抽样响应h[n]为

从式(2.2.28)可知累加器系统的单位抽样响应是单位阶跃序列,所以
y[n]=h[n]∗x[n]=u[n]∗x[n] (2.2.29)
则y(t)的离散时间傅里叶变换为
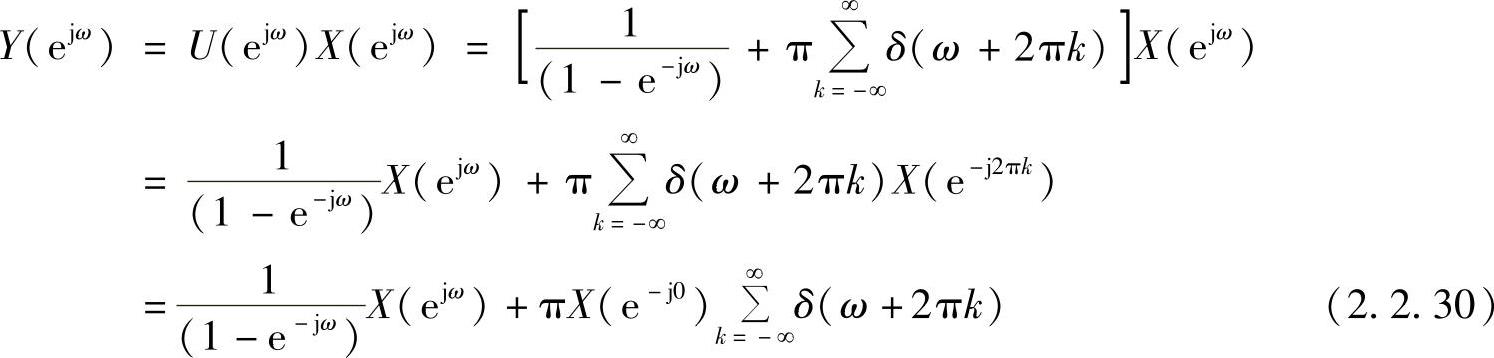
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




