离散时间傅里叶变换的定义和收敛性

离散时间傅里叶变换的定义为

从式（2.2.1）可以看出，序列的傅里叶变换的基函数e^jωn是定义在区间[-π，π]上的绝对可积函数空间的一组完备正交基，即

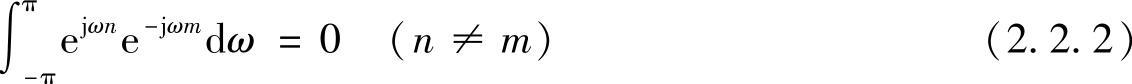
式（2.2.2）也称为两个函数的内积。又由于e^jωn=e^{j（ω+2π）n}，即e^jωn是ω以2π为周期的正交周期性函数，因此序列的傅里叶变换X（e^jω）也是以2π为周期的周期性函数，它是ω的连续函数。由于X（e^jω）的周期性，式（2.2.1）可以看做频域周期性函数X（e^jω）的傅里叶级数展开，其傅里叶系数就是x[n]。

对式（2.2.1）两边乘以e^jωm，然后在区间[-π，π]做积分，得

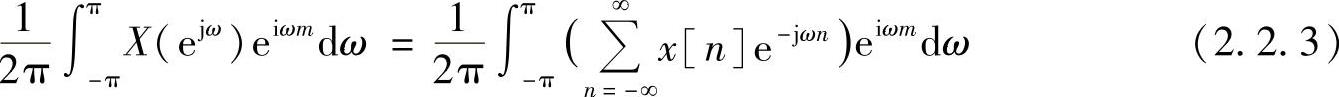
如果式（2.2.1）的展开式满足一致收敛条件，即

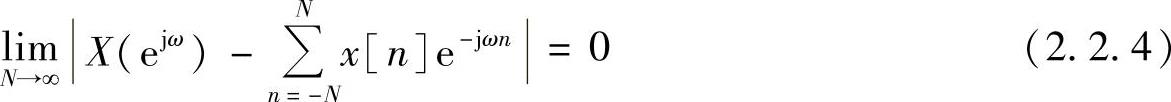
则按级数理论，求和符号和积分符号可以交换，从而得到

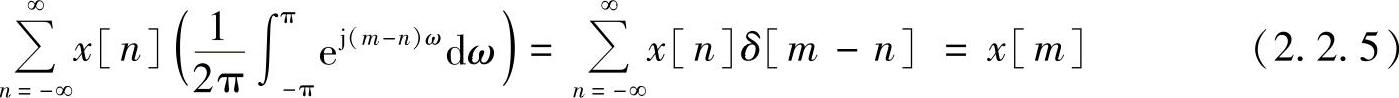
或表示成

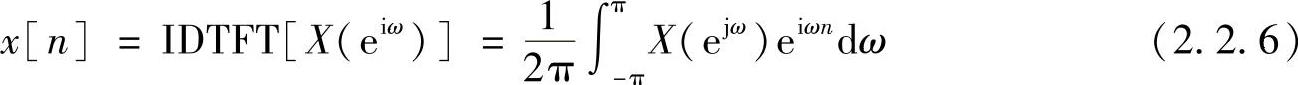
通常称式（2.2.1）为序列的傅里叶正变换，式（2.2.6）为X（e^jω）的傅里叶逆变换，用符号IDTFT表示。

X（e^jω）是ω的复函数，所以可以表示为

X（e^jω）=ReX（e^iω）+jImX（e^jω）=X_R（e^jω）+jX_I（e^jω）

=|X（e^jω）|e^{jargX（ejω）} （2.2.7）

X（e^jω）表示x[n]的频域特性，称为x[n]的频谱；|X（e^jω）|为幅度谱，φ（ω）=argX（e^jω）为相位谱，二者都是ω的连续函数，且是以2π为周期的周期性函数。

值得注意的是，如果式（2.2.1）的展开式不满足一致收敛条件，则可以定义z变换为

令z=re^jω，那么式（2.2.8）变为

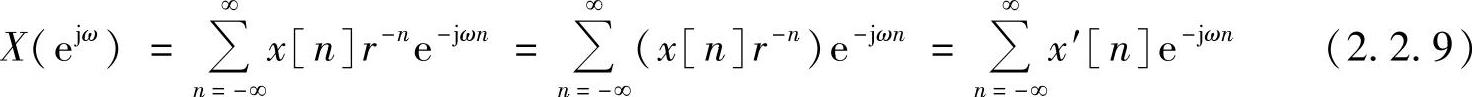
从式（2.2.9）可以看出，通过适当选取r的值，就能保证级数收敛。但需要注意，z变换不是两个无穷序列的内积，并且无穷序列之间不再是彼此正交。因此，z变换不具备正交变换的性质，但是，z变换对于研究离散系统的性质较方便，因此在离散系统分析中广泛应用。

【例2.2.1】 设x[n]是5点矩形序列，x[n]=R₅[n]，求它的傅里叶变换X[e^jω]。(www.xing528.com)

解 按定义式（2.2.1）直接写出R₅[n]的傅里叶变换式，得

式中，幅频特性为

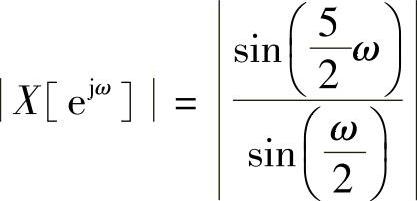
相频特性为

图2.2.1a～c分别画出了R₅[n]的波形、幅频特性和相频特性。

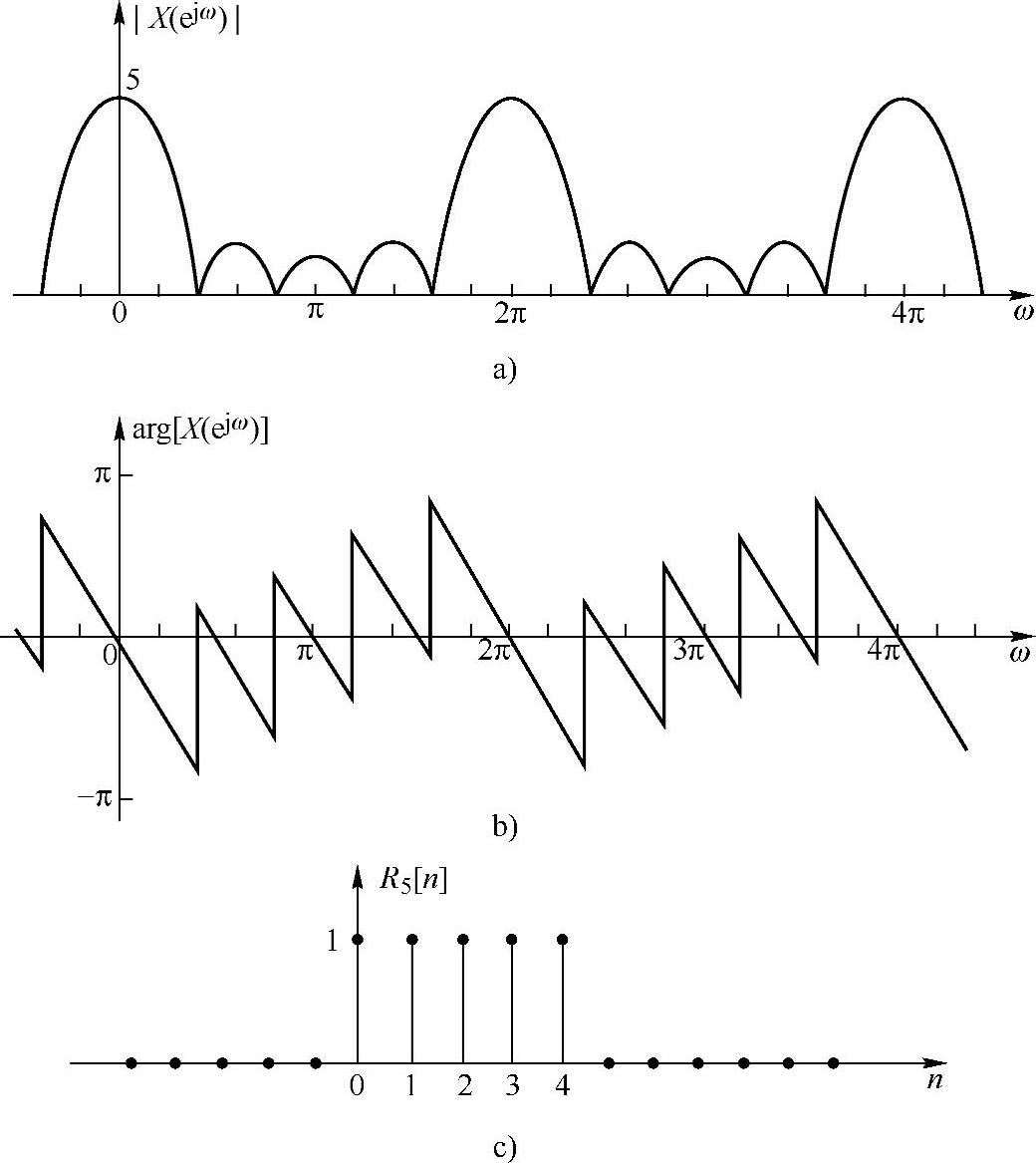
图2.2.1 序列R₅[n]的傅里叶变换

图2.2.2 理想低通滤波器特性

【例2.2.2】 给定如图2.2.2a所示的理想低通滤波器频率特性H（e^jω），求其傅里叶逆变换h[n]，即单位抽样响应。

解 按式（2.2.6）可得

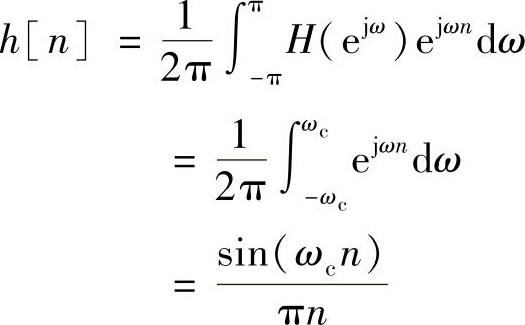
所求单位抽样响应h[n]如图2.2.2b所示。

x[n]绝对可和只是傅里叶变换存在的充分条件。式（2.2.1）所表示的频域傅里叶级数展开，只要其展开系数x[n]的表示式（2.2.6）存在，则X（e^jω）总是可以用傅里叶级数表示。例2.2.2是傅里叶变换的另一种情况，由H（e^jω）得出的h[n]不是绝对可和的，但h[n]的二次方可和，即

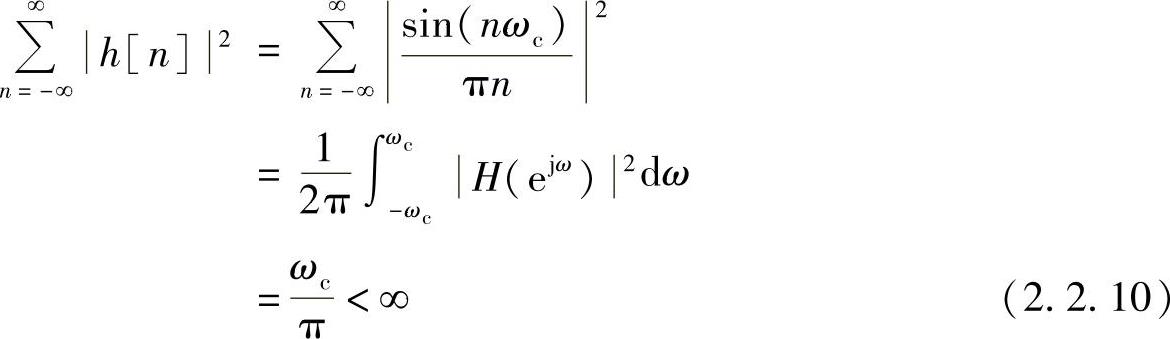
即h[n]是能量有限的，因此级数

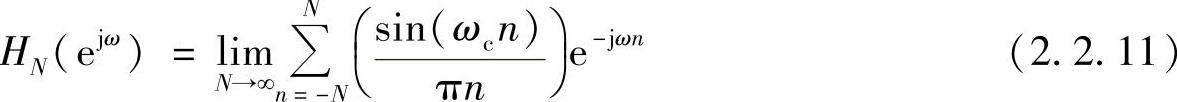
不能一致收敛于H（e^jω）。如图2.2.2c所示，在ω=ω_c的不连续点存在吉布斯（Gibbs）现象，式（2.2.1）表示的级数不能一致收敛于ω=ω_c的不连续点。但由于h[n]的二次方可和，从而导致式（2.2.1）对H（e^jω）以均方误差为零意义下的收敛，即

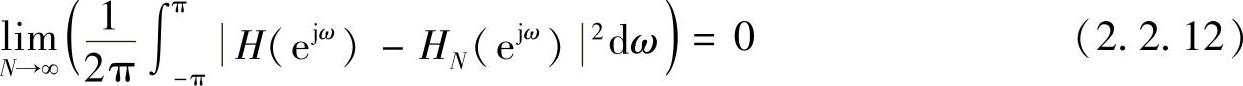
以上讨论的均匀一致收敛和均方误差为零方式收敛分别要求序列绝对可和或能量有限（绝对可和一定是能量有限，而能量有限不一定绝对可和），这是构成傅里叶变换存在的充分条件。不满足上列两个条件的某些序列（例如周期性序列），它们的傅里叶变换也可能存在，此时要引入奇异函数（即冲激函数）来表示傅里叶变换。