离散信号：连续时间信号的采样方法

在信号处理领域，采样是将信号从连续时间域上的模拟信号转换到离散时间域上的离散信号的过程。如果对模拟信号采样时间间隔是均匀的，即采样信号是周期性的，则称为均匀采样。模拟信号x_a（t）经采样后的离散信号表示为

x_a（nT）=x_a（t）|_t=nT=x[n] （1.6.1）由于是时域采样，信号频谱将由非周期性变成周期性频谱。

设原信号x_a（t）的傅里叶变换为

采样后序列的傅里叶变换为

按式（1.6.1）有

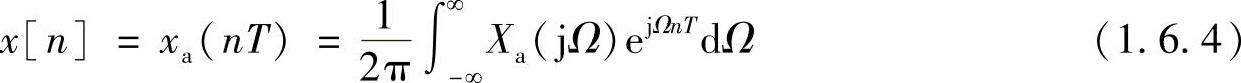
把上列积分进行一些变换，把Ω的积分区间分成无数邻接的子区间（见图1.6.1），中心位于，r为整数，于是有

图1.6.1 x_a（t）的傅里叶变换

令，同时设ω=Ω′T，则有

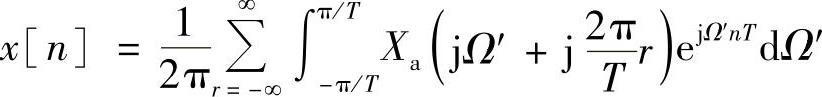
另外，序列x[n]的傅里叶逆变换为

对比式（1.6.6）有

式（1.6.8）表示连续信号和它的采样序列x[n]之间的傅里叶变换关系，即X（e^jω）是X_a（jΩ）在频域周期性重复叠加的结果，而数字角频率与模拟角频率满足ω=ΩT的关系，图1.6.2画出了二者频谱的关系。

若采样信号的周期（或采样信号频率，其中Ω₀是信号的最高角频率），则如图1.6.2b所示，X（e^jω）是X_a（jΩ）混叠的结果。若，则X（e^jω）周期性重复X_a（jΩ），没有频谱上的混叠，如图1.6.2c所示。满足采样频率是信号最高频率两倍的采样频率f_s，称为奈奎斯特采样率，即

图1.6.2 X_a（jΩ）与X（jω）之间的关系

这种情况下采样后序列的频谱可以表示为

限带的模拟信号用奈奎斯特采样率采样后，得到序列x[n]，由于频谱上不发生混叠，因而可以由x[n]来恢复原信号x_a（t），这只要让信号通过带宽为的低通滤波器即可。(https://www.xing528.com)

这一滤波过程也就是信号内插恢复过程（或称信号的重建过程）。

在满足奈奎斯特采样率的情况下，频谱不混叠，因而有

考虑到

得

式（1.6.11）表明，原信号x_a（t）是由一系列延时了的采样函数经加权后叠加而成，采样函数形式为

其加权系数是连续信号在采样点的采样值x_a（nT），因而在采样点处两者保持严格的一致，而其他点通过采样函数的内插来恢复，如图1.6.3所示。

用式（1.6.11）表示内插关系的另一优点是可以保持输入输出之间的卷积特性不变，如果连续系统有

当x_a（t）和h_a（t）代之以离散值x_a（nT）和h_a（nT）时，则采样后的y_a（nT）与x_a（nT）及h_a（nT）之间保持离散卷积和的关系，即

图1.6.3 由x_a（nT）恢复x_a（t）

这一关系意味着对连续时间线性时不变系统可以直接用离散时间线性移不变系统来实现。为此把式（1.6.13）表示成

可以证明上式中

因而有

令k=l+m并代入上式，得

可以看出y_a（t）离散化后与原x_a（nT）和h_a（nT）仍保持卷积关系。需要注意的是，连续系统离散化以后仍能维持卷积关系的条件是：①x_a（t）和h_a（t）必须是限带信号。②采样率满足奈奎斯特采样率，保证频谱不发生混叠。由上列采样关系得到的数字角频率ω与模拟角频率Ω之间满足线性关系ω=ΩT。