常系数线性差分方程的一般形式可表示为
式中,ak和br是常数,已知输入信号x[n]的位移阶次是M,输出响应y[n]的位移阶次即表示此差分方程的阶次N。
求解常系数线性差分方程的方法一般有以下5种:
(1)迭代法
包括手工计算逐次代入求解或利用计算机求解。这种方法概念清晰,比较简便,但只能得到其数值解,不能直接给出一个完整的解析表达式作为答案。
(2)时域经典法
与微分方程的时域经典法类似,先分别求齐次解与特解,然后代入边界条件求解待定的系数。这种方法便于从物理概念说明各响应分量之间的关系,但求解过程比较麻烦,在解决具体问题时不宜采用。
(3)分别求零输入响应与零状态响应
可以利用求齐次解的方法得到零输入响应,利用卷积和的方法求零状态响应。与连续时间系统的情况类似,卷积方法在离散时间系统分析中同样占有十分重要的地位。
(4)算子符号法
引入一系列算子及基于这些算子的运算,将差分方程转化为运算方程,从而简化差分方程的求解。算子符号法是由时域分析转向变换域分析的一种过渡形式。
(5)变换域方法
类似于连续时间系统分析中的拉普拉斯变换方法,利用z变换方法求解差分方程有许多优点,这是实际应用中简便而有效的方法。
下面将着重讨论时域经典法和求取零输入响应与零状态响应的方法。
1.时域经典法
差分方程的时域经典解法是把解分成齐次解yh[n]和特解yp[n],其完全解为
y[n]=yh[n]+yp[n] (1.5.14)
式(1.5.13)的差分方程对应的齐次方程为
可以证明其解具有yh[n]=Cαn的形式。称
a0αN+a1αN-1+…+aN-1α+aN=0 (1.5.16)
为上述差分方程的特征方程,此特征方程的根α1,α2,…,αN称为差分方程的特征根。在特征根没有重根的情况下,差分方程的齐次解为
yh[n]=C1αn1+C2α2n+…+CNαnN。 (1.5.17)
在有重根的情况下,齐次解的形式将略有不同。假定α1是特征方程的K重根,那么在齐次解中,相应于α1的部分将有K项,即
yh[n]=C1nK-1αn1+C2nK-2αn1+…+CK-1nαn1+CKαn1 (1.5.18)
当特征根为共轭复数时,齐次解的形式可以是等幅、增幅或衰减等形式的正弦(余弦)序列。
为求得特解,首先将激励函数x[n]代入方程式右端(也称自由项),观察自由项的函数形式来选择含有待定系数的特解函数式,将此特解函数代入方程后再求待定系数。一般情况下,若激励函数代入方程式右端出现nk形式的函数,则特解选
yp[n]=D0nk+D1nk-1+…+Dk (1.5.19)
出现an形式的函数,且a不是此差分方程的特征根,则特解选
yp[n]=Dan (1.5.20)
a是此差分方程的特征单根,则特解选
yp[n]=(D1n+D0)an (1.5.21)
a是此差分方程的r重特征单根,则特解选
yp[n]=(Drnr+Dr-1nr-1+…+D1n+D0)an (1.5.22)
在一般情况下,对于N阶差分方程,应给定N个边界条件,例如取y[0],y[1],…,y[N-1]。利用这些条件,代入完全解(齐次解+特解)的表达式,可以构成一组联立方程,求得N个系数C1,C2,…,CN。考虑没有重根的情况,此时方程的全解为
y[n]=C1αn1+C2αn2+…+CNαnN+D[n] (1.5.23)
式中,D[n]表示它的特解,其余各项之和为齐次解。引用边界条件可建立如下方程组
将此方程组写作矩阵形式
简写作
Y[k]|N×1-D[k]|N×1=VN|×NC|N×1 (1.5.26)
借助范德蒙特(Vandermonde)逆矩阵V-1可求得系数C的一般表达式为
C=V-1{Y[k]-D[k]} (1.5.27)
【例1.5.4】 求差分方程y[n]+2y[n-1]=x[n]-x[n-1]的完全解,其中x[n]=n2,y[-1]=-1。
解
由特征方程α+2=0得特征根为α=-2,所以有
yh[n]=C1(-2)n
激励信号=n2-(n-1)2=2n-1,故选特解为yp[n]=D0n+D1。
代入差分方程得
D0n+D1+2D0(n-1)+2D1=2n-1
3D0n+3D1-2D0=2n-1
解出系数为
所以
代入边界条件,求待定系数C1
得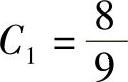
完全解的闭合表达式为
【例1.5.5】 求差分方程y[n]+y[n-1]-6y[n-2]=x[n]-x[n-1]的完全解,其中激励函数x[n]=n2-2n,且已知y[1]=1,y[2]=1。
解
由特征方程α2+α-6=0得特征根α1=2,α2=-3,所以有
yh[n]=C12n+C2(-3)n
激励信号=n2-2n-[(n-1)2-2(n-1)]=2n-3,故选特解为yp[n]=D0n+D1,代入差分方程得
D0n+D1+D0(n-1)+D1-6[D0(n-2)+D1]=2n-3
-4D0n-4D1+11D0=2n-3
比较两边系数得
所以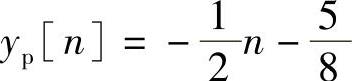
代入边界条件y[1]=1和y[2]=1,求待定系数C1和C2
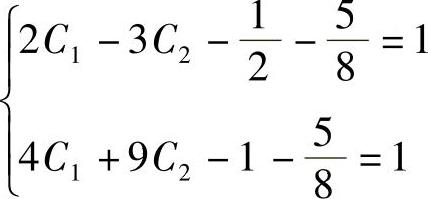 得
得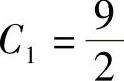 ,
,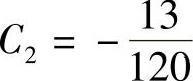 完全解的闭合表达式为
完全解的闭合表达式为
【例1.5.6】 已知差分方程y[n]+3y[n-1]+2y[n-2]=x[n]-x[n-1],初始条件为y[0]=0,y[1]=0,激励信号为
求其完全响应。
解
由特征方程α2+3α+2=0得特征根α1=-1,α2=-2,所以有
yh[n]=C1(-1)n+C2(-2)n
此类问题需分区考虑初始条件:
x[-1]=0,x[0]=1,x[1]=-2,x[2]=4,y[0]=0,y[1]=0
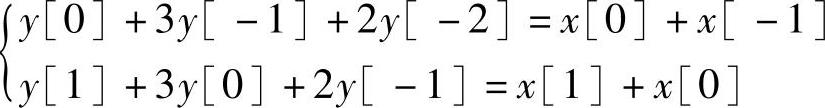 解得
解得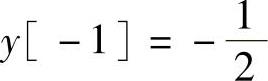 ,
,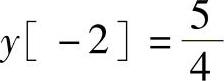 当n<0时(https://www.xing528.com)
当n<0时(https://www.xing528.com)
完全响应为y[n]=C1(-1)n+C2(-2)n代入初始条件得
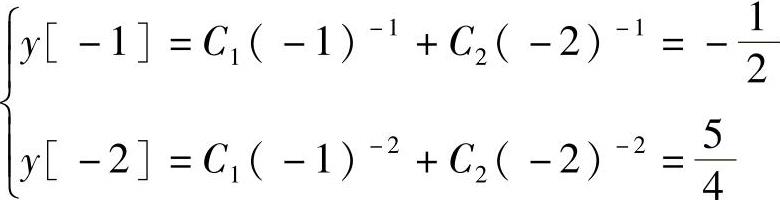 解得
解得 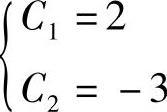
所以有
y[n]=2(-1)n-3(-2)n
当n=0时
因为x[n]=δ[n],故选特解为yp[n]=D,代入差分方程得
D+3D+2D=1
解出系数为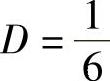 ,所以有
,所以有
代入初始条件y[0]=0,y[1]=0,得
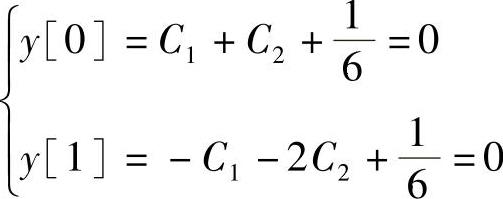 解得
解得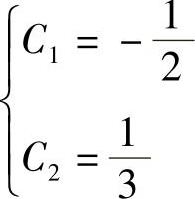
所以 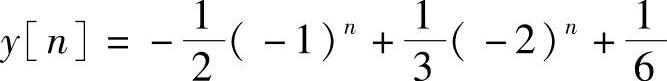
当n≥1时
因为-2是差分方程的特征单根,所以有
yp[n]=(D1n+D0)(-2)n
代入差分方程化简得
解出D1=1,D0=0,所以有
yp[n]=n(-2)n
应用递推法,从差分方程可得
y[2]+3y[1]+2y[0]=x[2]-x[1]求出y[2]=6
完全响应为y[n]=yh[n]+yp[n]=C1(-1)n+C2(-2)n+n(-2)n,代入初始条件y[1]=0,y[2]=6,得
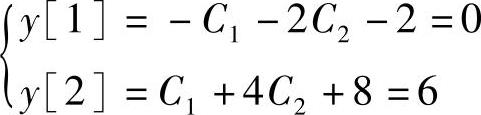 求出 C1=-2,C2=0
求出 C1=-2,C2=0
所以y[n]=-2(-1)n+n(-2)n
2.求零输入响应与零状态响应的方法
重写式(1.5.26)如下:
Y[k]|N×1-D[k]|N×1=V|N×NC|N×1
响应的边界条件y[k]可以分解为零输入响应的边界值yzi[k]与零状态的边界值yzs[k]两部分,即y[k]=yzi[k]+yzs[k],在零输入条件下有D[k]=0,于是得到相应的系数Czi值矩阵表示为
Czi=V-1Yzi[k] (1.5.28)
而在零状态下,系数Czs值矩阵表示为
Czs=V-1{Yzs[k]-D[k]}=V-1{Y[k]-Yzi[k]-D[k]} (1.5.29)
系数C与Czi、Czs之间满足
C=Czi+Czs (1.5.30)
于是完全响应由以下两部分组成:
零输入响应:
零状态响应:
还需指出,差分方程的边界条件不一定由y[0],y[1],…,y[N-1]这一组数字给出。对于因果系统,常给定y[-1],y[-2],…,y[-N]为边界条件。若激励信号在n=0时接入系统,所谓零状态是指y[-1],y[-2],…,y[-N]都等于零(N阶系统),而不是指y[0],y[1],…,y[N]为零。
【例1.5.7】 已知系统的差分方程表达式为
y[n]+2y[n-1]=u[n]
且y[-1]=1,求系统的零输入响应、零状态响应和完全响应。
解
1)求零状态响应,令y[-1]=0。
由系统的特征方程α+2=0,可得齐次解为C(-2)n,而特解为D,完全解的形式为y[n]=C(-2)n+D。将特解代入方程得D+2D=1,D=1/3。将y[0]=1代入求C:C+D=1,所以C=2/3。因此系统的零状态响应为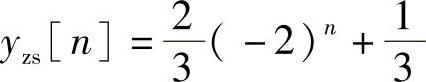 。
。
2)求零输入响应,令激励信号为0。
容易写出零输入响应为yzi[n]=Czi(-2)n,将y[-1]=1代入得Czi=-2,因此零输入响应y[n]=(-2)n+1。
3)系统的完全响应为
当差分方程阶次较低时,通常也用迭代法求解差分方程,比如差分方程为
y[n]=ay[n-1]+x[n],其中x[n]=δ[n],y[-1]=0,求其系统响应。
n=0 y[0]=ay[-1]+x[0]=0+δ[n]=1
n=1 y[1]=ay[0]+x[1]=a+0=a
n=2 y[2]=ay[1]+x[2]=a·a+0=a2
︙
n=ny[n]=ay[n-1]+x[n]=an
所以 y[n]=anu[n]
3.单位抽样响应
单位抽样响应属于零状态响应。在连续时间系统中,研究单位冲激δ(t)作用于系统引起的响应h(t)可以便于求取系统在任意信号作用下的响应。对于离散系统,基于同样的原因考察单位抽样序列δ[n]作为激励而产生的系统响应h[n]——单位抽样响应。
求取单位抽样响应时,可以把单位抽样激励信号等效为起始条件,这样就把问题转化为求解齐次方程。
由于单位抽样响应h[n]表征了系统自身的性能,因此,在时域分析中可以根据h[n]来判断系统的某些重要特征,如因果性、稳定性,以此区分因果系统和非因果系统,稳定系统和非稳定系统。
离散线性移不变系统作为因果系统的充分必要条件为
h[n]=0 (当n<0)
或
h[n]=h[n]u[n]
离散线性移不变系统作为稳定系统的充分必要条件为
既满足稳定条件又满足因果条件的系统是主要研究对象,这种系统的单位抽样响应h[n]是单边的而且是有界的,即
【例1.5.8】 已知系统的差分方程y[n]+y[n-1]-6y[n-2]=x[n]-x[n-1],求系统的单位抽样响应。
解
1)求齐次解。由特征方程α2+α-6=0解得α1=2,α2=-3,所以有
yh[n]=C12n+C2(-3)n
2)假定差分方程式右端只有x[n]项作用,不考虑x[n-1]项作用,求此系统的单位抽样响应h1[n]。因为起始时系统是静止的,容易推知h1[-2]=h1[-1]=0,h1[0]=δ[0]=1,h1[1]=-1。以h1[0],h1[1]作为边界条件建立方程组
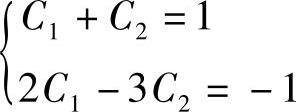 解得系数
解得系数 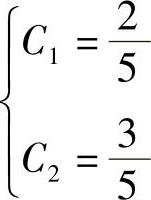
所以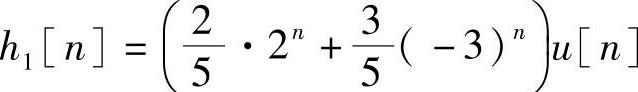
3)只考虑x[n-1]项作用引起的响应h2[n]。由线性移不变特性可知
4)将以上结果叠加,得到系统的单位抽样响应为
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




