离散时间系统的状态空间表述方式

系统的输入输出关系表示只考虑了系统的外部特性，但在很多情况下，还是希望知道系统的内部特性。比如，在数字系统中，由于计算过程中可能会有字长不够的问题，需要对系统内部状态进行分析；复杂数字系统因为在线测试的需要，要对处理过程中的中间结果进行监视等。

状态空间法是时间域方法，所以很适合于用计算机来计算。状态空间法能揭示系统内部变量和外部变量间的关系，因而有可能找出过去未被认识的系统的许多重要特性，其中能控性和能观测性尤其具有特别重要的意义。

图1.5.5 流图状态变量选取

在离散系统中，往往取延迟单元的输出作为状态变量，如图1.5.5所示，每个延时单元对应着一个状态变量。选定状态变量之后，就可以写出关于选定状态和输出的一阶差分方程，系统的状态空间表示。以图1.5.5表示的二阶系统流图为例，其状态方程和输出方程为

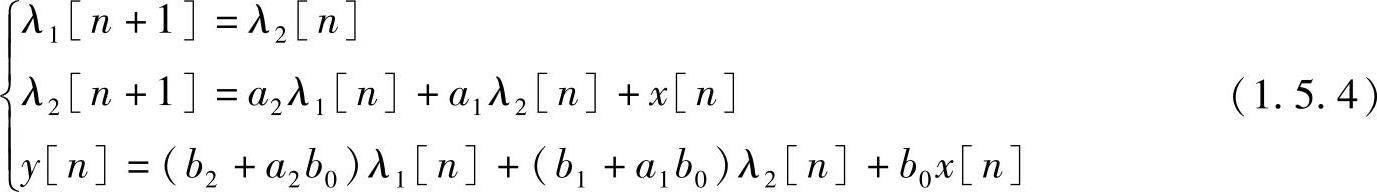
表示成矢量方程形式为

通常式（1.5.5）称为状态方程，且表示成

或

λ[n+1]=Αλ[n]+Βx[n] （1.5.8）

式（1.5.6）称为输出方程，表示为

式（1.5.7）和式（1.5.9）中，λ[n+1]表示系统状态矢量，y[n]表示系统输出，A、B、C和D分别表示相应矩阵。

对于一般多输入-多输出系统，状态方程和输出方程形式都是相同的，可表示为

或表示为

式中

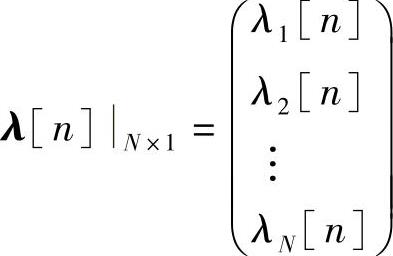
称为状态矢量，状态矢量所在的空间称为状态空间；

是N阶方阵，称为系统的特征矩阵；

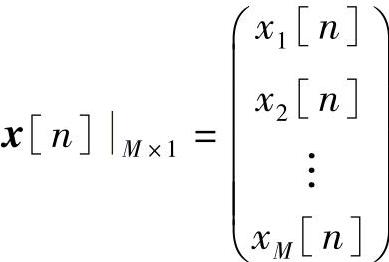
是M个输入信号列矢量；

是表示输入信号与状态矢量之间关系的矩阵；

是L个输出信号的矢量；(www.xing528.com)

是表示输出信号与状态矢量之间关系的矩阵；

是表示输入信号与输出信号之间关系的矩阵。

上述状态方程可用结构框图表示，如图1.5.6所示。由式（1.5.12）可知，离散系统用状态方程描述时，它的特性完全由A、B、C和D矩阵所确定。

图1.5.6 状态方程表示的结构框图

有很多方法可以得到离散系统的状态方程。式（1.5.5）和式（1.5.6）是根据系统的信号流图来编写状态方程，另外也可以根据系统的系统函数来直接编写系统的状态方程。

【例1.5.3】 对于用差分方程表示的离散系统

求其系统的状态方程。

解

对于给定的差分方程，两边求z变换，得

令

则

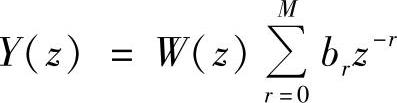
再分别求逆z变换，得

把序列{w[n]}的各项延迟结果取为状态变量，即

则有

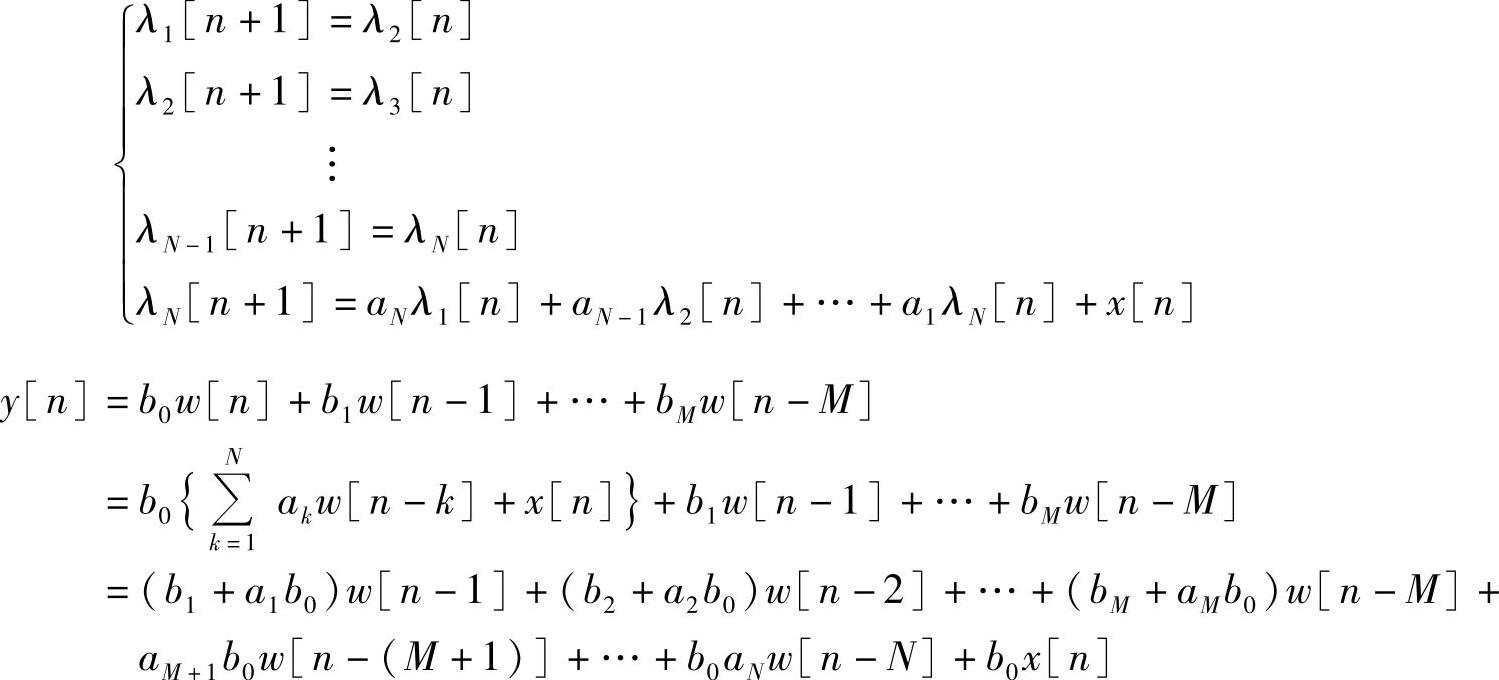
把状态变量代入上式，得输出方程为

y[n]=a_Nb₀λ₁[n]+a_N-1b₀λ₂[n]+…+a_M+1b₀λ_N-M[n]+（b_M+a_Mb₀）λ_N-M+1[n]+…+（b₂+a₂b₀）λ_N-1[n]+（b₁+a₁b₀）λ_N[n]+b₀x[n]

把状态方程和输出方程写成矢量方程形式为

例1.5.3给出的差分方程转换为状态方程的方法并不是唯一的，如果把H（z）用部分分式展开成并联结构形式，就可以得出另一种状态方程。事实上当给定系统的转移函数H（z）后，可以有多种形式的状态方程与之对应，在此不再赘述。