全通系统与最小相位系统：比较与优化

以上对稳定、因果性系统H（z）的分析中，并没有对其零点做任何约束，一般情况下给定系统的幅频特性|H（e^jω）|，可以有多个H（e^jω）与之对应，也就是不同的零点分布，可以有不同的相频特性与之对应。在众多的数字系统中，全通系统和最小相位系统在理论上和实践上都有特殊的意义。

全通系统定义为：如果一个因果系统的幅频响应对所有的频率都等于1（或者一个常数），即

|H（e^jω）|=1 （0≤|ω|≤π） （1.4.33）

则称系统H（z）为全通系统。

全通系统的频率响应还可表示为

H（e^jω）=e^jθ（ω） （0≤|ω|≤π） （1.4.34）

显然

H（z）=z^-k （1.4.35）

是最简单的全通系统，也是一纯延迟系统。

一阶全通系统可表示为

该系统的极点z_p=λ，零点z_z=1/λ，零、极点成镜像对称关系。

二阶全通系统可表示为

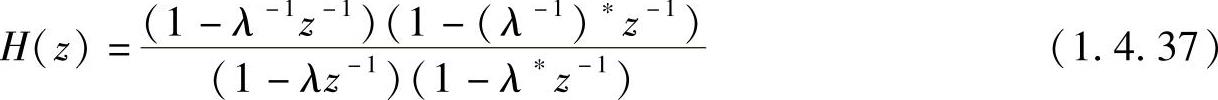
对于单位圆内的共轭极点，一对共轭零点和极点以单位圆为镜像对称。

N阶全通系统可表示为

或者

图1.4.10 全通系统的零、极点分布(www.xing528.com)

从式（1.4.39）可以看到全通系统零、极点分布的特点：如z_k为一个极点，则z^∗_k也是一个极点，1/z_k和1/z^∗_k必为系统零点，如图1.4.10所示。

由于

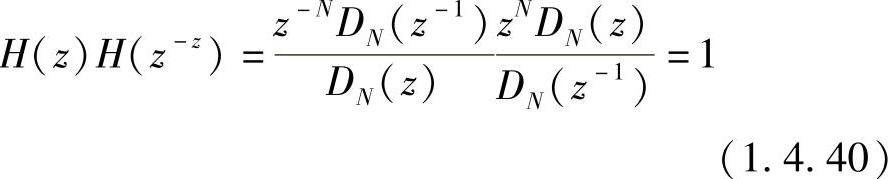
式中，令z=e^jω，则

|H（e^jω）|2=H（e^jω）H（e^-jω）=1 （1.4.41）从式（1.4.41）可知，该系统满足全通系统的条件。

此外，全通系统的相位有如下的特性：

性质1 全通系统相位特性θ（ω）随频率单调下降，即

性质2 对实稳定全通系统，当频率ω从0变化到π时，N阶全通系统的相位的改变为Nπ。

在实际应用中另一类重要的系统是最小相位系统，它定义为零、极点都在单位圆内的系统称为最小相位系统。这里的“最小相位”是相对于至少有一个零点在单位圆外的系统而言，当ω从0变化到2π时，最小相位系统具有最小的相位变化量。

设系统具有M个零点，单位圆内有m_i个，单位圆外有m_o个，有N个极点，单位圆内有n_i个，单位圆外有n_o个。对稳定系统n_o=0，N=n_i。当ω从0变化到2π时，稳定系统的相位改变量为

Δarg[H（e^jω）]=2π（N-M）+2π（m_i-N）

=2π（m_i-M）=-2πm_o （1.4.43）

当系统函数的所有零点都在单位圆内时m_o=0，所以，当ω从0变化到2π时，最小相位系统的相位改变量为0。

最小相位系统有下列几个主要特性：

性质1 任何非最小相位系统都可以由最小相位系统和全通系统相级联构成。即

H（z）=H_min（z）H_A（z） （1.4.44）

式中，H（z）为非最小相位系统；H_min（z）为最小相位系统；H_A（z）为全通系统的系统函数。

性质2 最小相位系统具有最小群延时和最小相位滞后特性。即最小相位系统的相位滞后总是小于所有其他具有相同幅频特性的系统的相位滞后，这也就是最小相位系统名称的来由。

推论 全通系统的相位在[0，π]范围内为非正值。

性质3 最小相位系统具有能量延时最小的特性。