离散时间系统变换域分析

系统的变换域分析是利用z变换或傅里叶变换对系统的性能进行分析。对于线性移不变系统，变换域分析方法更能简洁明了地表现出系统的各项性能。

线性移不变系统的主要性质往往可以用系统函数H（z）来体现。线性移不变系统的系统函数H（z）定义为：系统在零状态情况下，输出序列的z变换与输入序列的z变换之比，即

实际上它就是单位抽样响应h[n]的z变换，即

对于用差分方程形式给出的线性移不变系统，其输入输出关系为

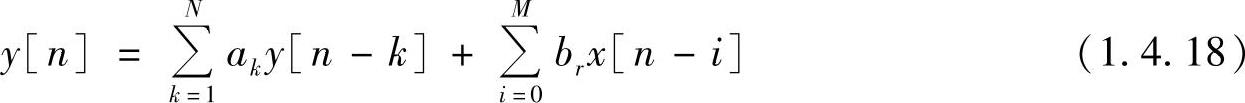
对方程两边取零状态下的z变换，就可以得到系统的系统函数为

如果对式（1.4.19）的分子、分母多项式进行因式分解，则有

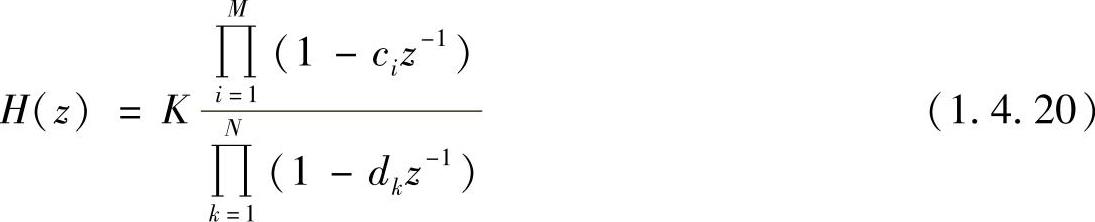
式中，c_i和d_k分别为H（z）的零点和极点。因此除了一个常数K之外，系统函数可完全由它的零、极点来决定。零、极点的分布及H（z）的收敛域决定了系统的很多特性，我们把这种分析方法称为零、极点分析法。

1.零、极点分布与系统的稳定性和因果性

对于线性移不变系统，在有界输入产生有界输出意义下稳定的充要条件是h[n]绝对可和，即

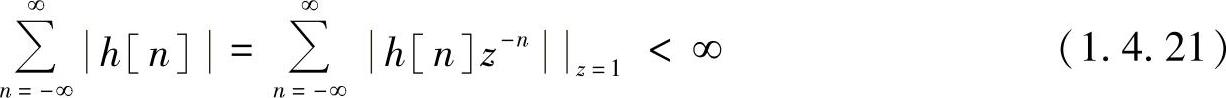
这表明稳定系统的系统函数H（z）的收敛域包含单位圆。

线性移不变系统是因果的，它的充分必要条件是h[n]=0（n＜0）。这一条件意味着H（z）的收敛域必须是某一圆外的全部z平面，包括z=∞在内，即

Rx-＜z≤∞ （1.4.22）

综合上述两点，如果系统是稳定因果系统，则系统函数H（z）的极点都必须在单位圆内。所以系统函数的极点分布与收敛域共同决定了系统的特性。

2.零、极点分布与系统的可逆性

给定线性移不变系统的系统函数H（z），它的逆系统的系统函数由式（1.4.15）关系可以得出

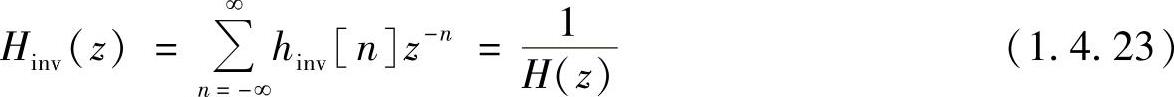
若H（z）由式（1.4.20）给出，则其对应的逆系统的系统函数为

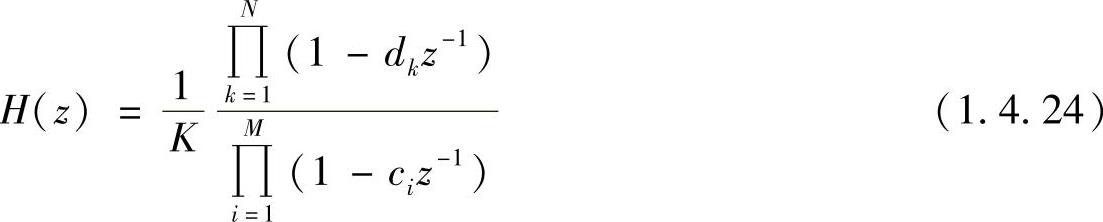
可见H（z）的零点c_i成为H_inv（z）的极点；H（z）的极点d_k成为H_inv（z）的零点。而H_inv（z）的收敛域，受到式（1.4.23）给出的关系约束，即

H（z）·H_inv（z）=1 （1.4.25）

式（1.4.25）成立的条件是H（z）和H_inv（z）有共同的收敛域，如果两者没有共同的收敛域，则原系统是不可逆的。

【例1.4.8】 已知某系统的系统函数为

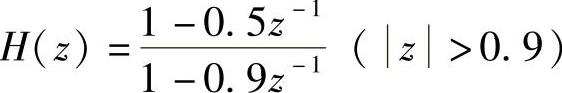
问系统是否可逆，若可逆，求出对应的h_inv[n]。

解 逆系统的系统函数是

由于H_inv（z）只有一个极点z_p=0.5，因而其收敛域只有两种可能：|z|＞0.5和|z|＜0.5。当|z|＞0.5时收敛域与H（z）有共同部分，因而H（z）的逆系统存在，而且逆系统对应的单位抽样响应为

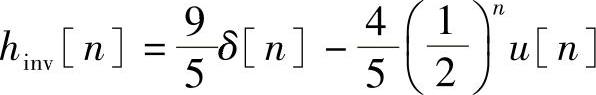
这一逆系统是稳定的而且是因果的。若H_inv（z）的收敛域|z|＜0.5，则与H（z）没有共同的收敛域，此时的H_inv（z）不能作为H（z）的逆系统。(www.xing528.com)

由式（1.4.23）可以得出，如果H（z）的所有零、极点位于单位圆内，即系统是稳定的因果性系统，则它的逆系统存在，而且是稳定的因果性系统。这种系统就是最小相位系统。

3.零、极点分布与系统的频率特性

系统的频率特性定义为：当输入为不同频率的正弦序列或复指数序列e^jωn时，系统的稳定响应与输入信号角频率ω之间的关系。对线性移不变系统，有

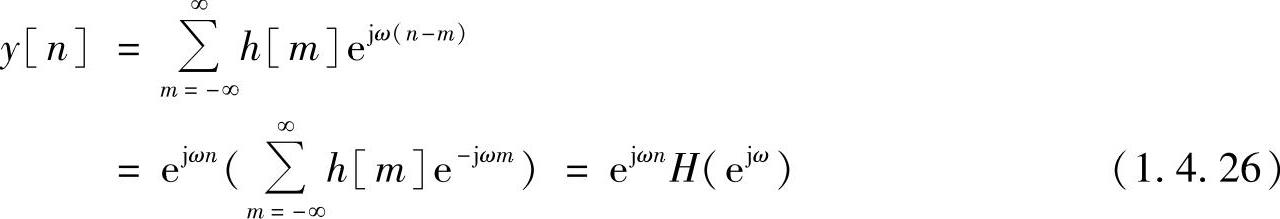
式中，H（e^jω）就是系统的频率特性。式（1.4.26）表明系统在稳定情况下，对e^jωn的输入信号，输出仍是e^jωn的形式，只不过被系统频率特性H（e^jω）加权。凡是具备这种特性的输入信号称为该系统的本征函数，对应的加权系数称为本征值。因而e^jωn是线性移不变系统的本征函数之一，对应的本征值H（e^jω）是系统的频率特性。

从频率特性的定义可以得出

也就是说系统的频率特性是单位抽样响应的傅里叶变换。如果系统是稳定的，其收敛域包含单位圆，则傅里叶变换存在，也就是说z变换在单位圆上的特性构成了系统的频率特性。

系统的频率特性可以根据系统函数H（z）的零、极点分布由几何方法直接地确定。在式（1.4.20）中，令z=e^jω，则有

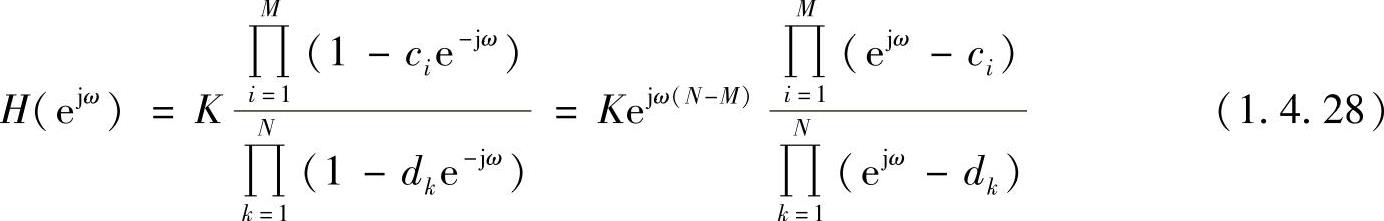
根据图1.4.7所示的几何关系，令

其中B点位于单位圆上，表示任意角频率ω，Qi和φ_i分别为矢量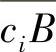的模和相角，而P_k和θ_k分别为矢量d_kB的模和相角。于是

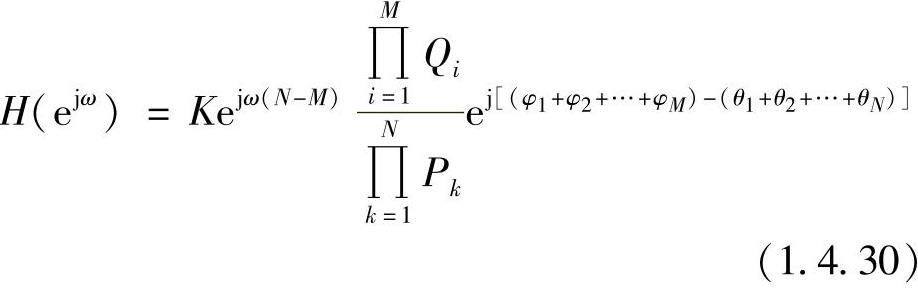
因此系统的幅频特性为

系统的相频特性为

arg[H（e^jω）]=arg[K]+ω（N-M）+（φ₁+φ₂+…+φ_M）-（θ₁+θ₂+…+θ_N） （1.4.32）

由式（1.4.31）可以看出：①当频率点变到极点附近时，P_k就变小，在该极点附近的频率就会出现峰值，极点越接近单位圆，峰值就越尖锐；同样，当频率点变到零点附近时，Q_i就变小，在该零点附近的频率就会出现低谷，当零点在单位圆上时，该零点就是传输零点。可见在单位圆附近的零极点对系统的幅频特性有较大的影响。②零点可在单位圆内、外，但极点只能在单位圆内，否则系统将不稳定。③而系统的相位响应对幅频特性没有影响。

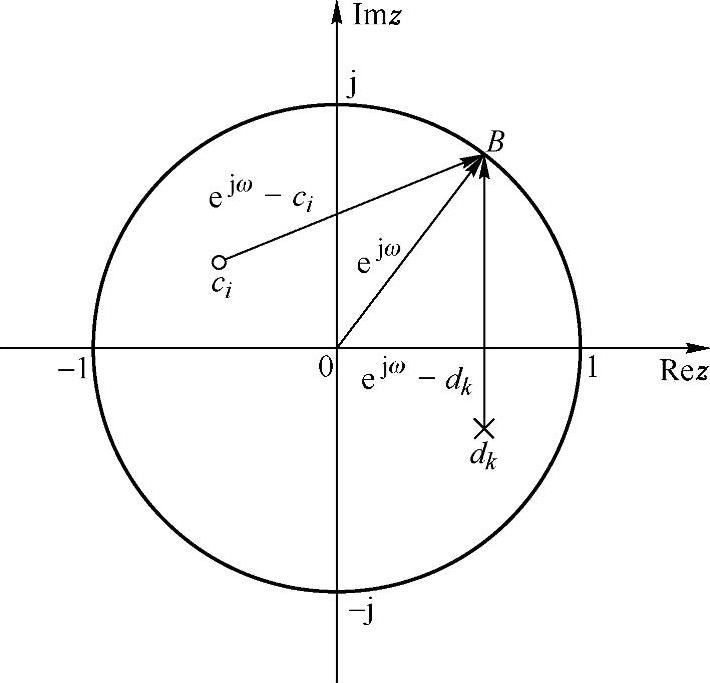
图1.4.7 频率特性的几何法确定

【例1.4.9】 已知系统的差分方程为y[n]-ay[n-1]=x[n]（0＜a＜1），指出系统函数的零、极点并分析系统的频响特性。

解 系统的传输函数为

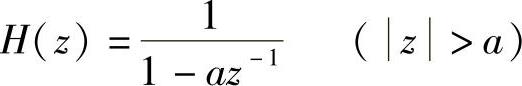
所以，系统的极点z_p=a，零点z_z=0，其分布如图1.4.8所示。由图可知，当e^jω在单位圆上从ω=0逆时针旋转一周时：①在ω=0处，极点到单位圆的距离最短，所以ω=0频率点幅度最大，成为波峰。②在ω=π时，极点到单位圆的距离最长，所以ω=π频率点幅度最小，成为波谷。③在原点处的零点，对幅频特性没有影响。

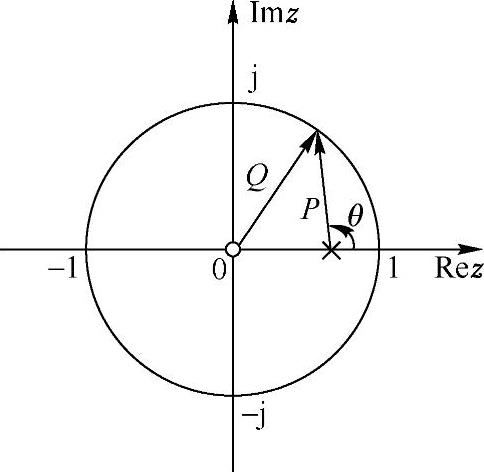
图1.4.8 一阶系统零、极点分布

对应的幅频特性和相频特性为

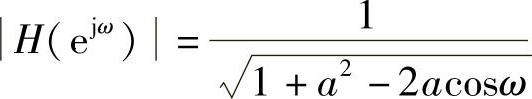
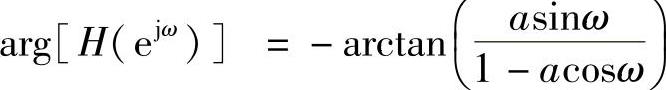
其幅频和相频特性如图1.4.9所示。

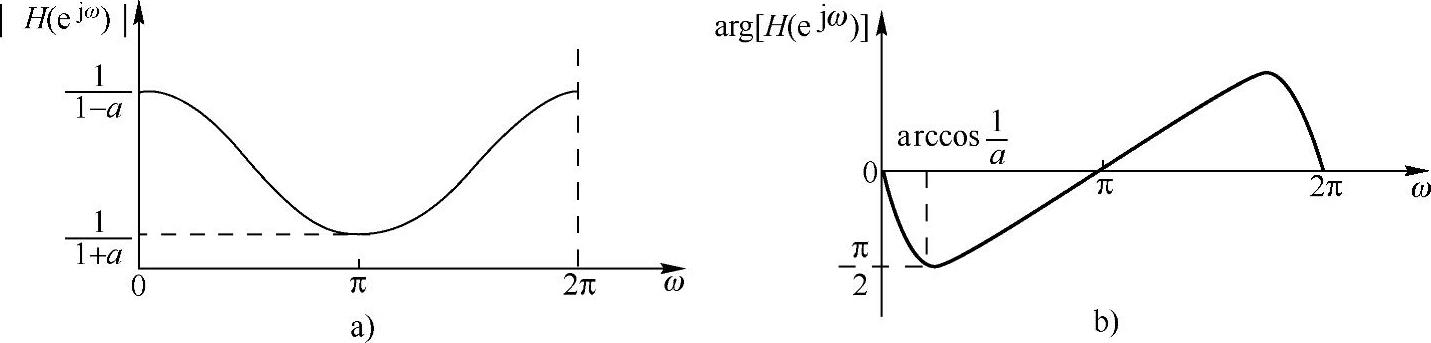
图1.4.9 一阶系统幅频和相频特性