线性移不变系统的特性探析

既满足线性，又满足移不变条件的系统是线性移不变系统。这是一种最常用、也最容易理论分析的系统。这里约定：此后如不加说明，所说的系统均指线性移不变系统，简称LSI系统。对于线性移不变系统，很多特性可以用它的单位抽样响应h[n]来表征。

系统单位抽样响应定义为：当系统的输入是单位抽样序列δ[n]时，系统的零状态输出称为单位抽样响应，用h[n]表示。

单位抽样响应是系统固有的，反映了系统特征，即

h[n]=T{δ[n]} （1.4.3）

由于任何输入序列都可写成以自身为权值的、抽样序列δ[n-n₀]的x[n]加权和，即

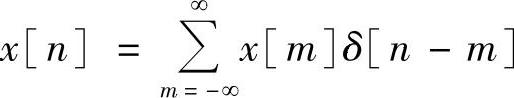
由线性移不变特性，对照式（1.4.3）可得

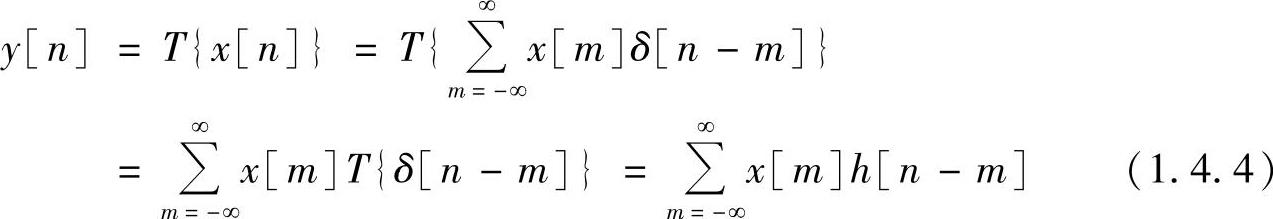
式（1.4.4）说明线性移不变离散系统的输出序列等于输入序列和系统单位抽样响应的线性卷积和。

线性移不变系统的串、并联关系可以由卷积和性质导出。

卷积和满足交换律

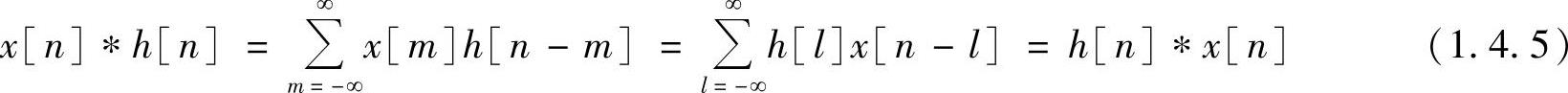
这说明对线性移不变系统，单位抽样响应h[n]和输入信号x[n]可以相互交换位置，即用x[n]表示系统单位抽样响应，以h[n]作为系统的输入，其效果和原来一样。这也进一步说明了信号与系统的等价性，即信号就是系统，系统就是信号。

卷积和满足结合律

x[n]∗h₁[n]∗h₂[n]=x[n]∗（h₁[n]∗h₂[n]） （1.4.6）

式（1.4.6）可记为h[n]=h₁[n]∗h₂[n]，这表明系统级联总的单位抽样响应h[n]等于各级联子系统单位抽样响应的卷积和，如图1.4.3所示。

图1.4.3 系统的级联

卷积和满足分配律

x[n]∗（h₁[n]+h₂[n]）=x[n]∗h₁[n]+x[n]∗h₂[n] （1.4.7）

式（1.4.7）可记为h[n]=h₁[n]+h₂[n]，这表示系统并联总的单位抽样响应h[n]等于各子系统单位抽样响应之和，如图1.4.4所示。

当一个系统被确定为线性移不变系统后，它的稳定性和因果性就可以用单位抽样响应h[n]唯一确定。

如果一个线性移不变系统是稳定的，它的充分必要条件是单位抽样响应h[n]绝对可和，即

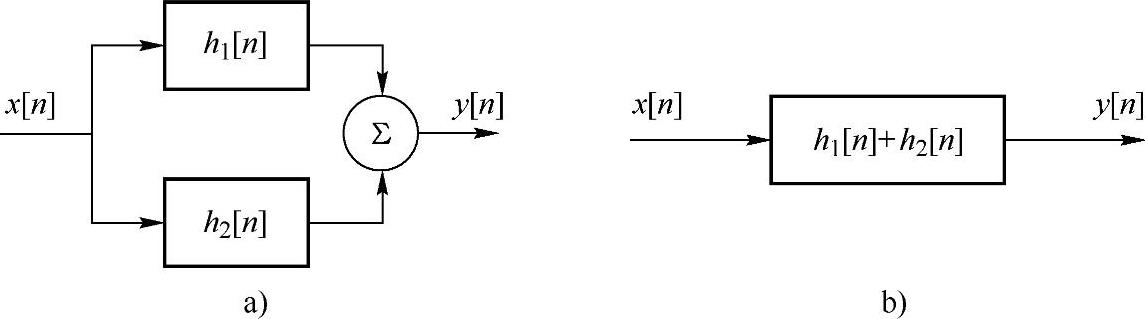
图1.4.4 系统的并联

式中，S为有限正值。

证明 充分性：设输入x[n]是有界的，且对全部n满足x[n]≤B_x，则(www.xing528.com)

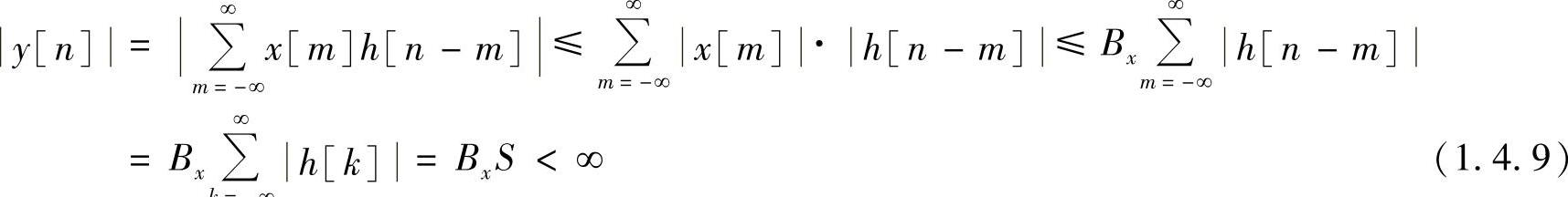
这表明，若系统的单位抽样响应h[n]绝对可和，则有界输入一定对应有界输出，系统是稳定的。

必要性：利用反证法。如果系统稳定，但是有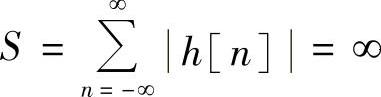，则系统对下列有界输入信号

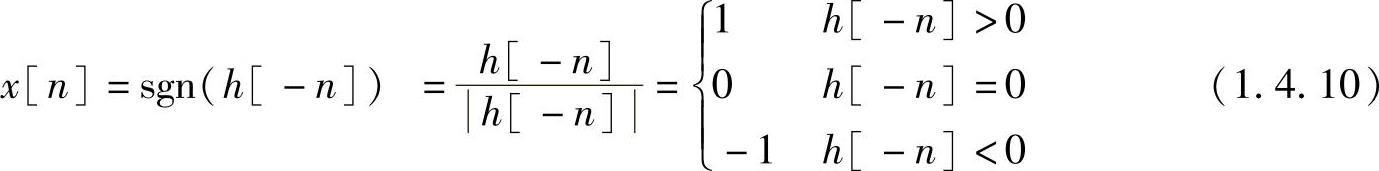
对应的输出响应在n=0时的值为

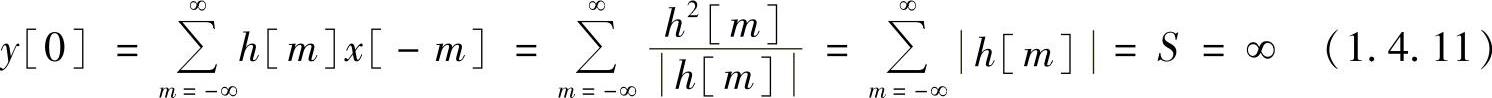
这与假设是矛盾的，因而若系统稳定，必有单位抽样响应h[n]绝对可和。

如果一个线性移不变系统是因果的，则它的充分必要条件是

h[n]=0 （n＜0） （1.4.12）

证明 把y[n]改写为两项求和形式，即

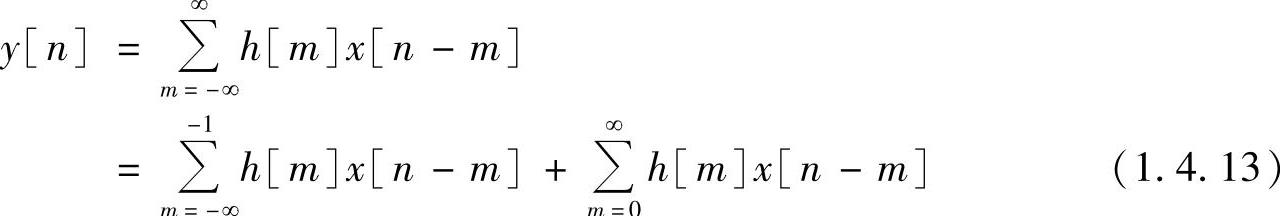
式中，第一求和项表示与x[n]将来值有关的项；第二求和项表示与x[n]的当前输入及以前输入有关的项。

充分性：若h[n]=0，n＜0，则式（1.4.13）中第一求和项恒为零，系统的响应只和第二求和项有关，因而系统是因果的。

必要性：如果系统是因果的，则y[n]只与x[n]的当前输入值及以前输入值有关，与x[n]将来输入值无关，因而式（1.4.13）中第一求和项必等于零。要保证这一点，只有h[n]=0，n＜0条件成立。必要性得证。

在数字信号处理系统中，非因果前项差分系统通过级联一个延时系统就能把它转换成因果系统。例如，y[n]=x[n+1]-x[n]，该系统是非因果的，其单位抽样响应如图1.4.5a中h₂[n]，但如果与h₁[n]=δ[n-1]的单位延时因果系统相级联，则系统的单位抽样响应为

h[n]=h₁[n]∗h₂[n]=δ[n-1]∗（δ[n+1]-δ[n]）

=δ[n]-δ[n-1] （1.4.14）

整个级联系统是一因果的后向差分系统，如图1.4.5b所示。

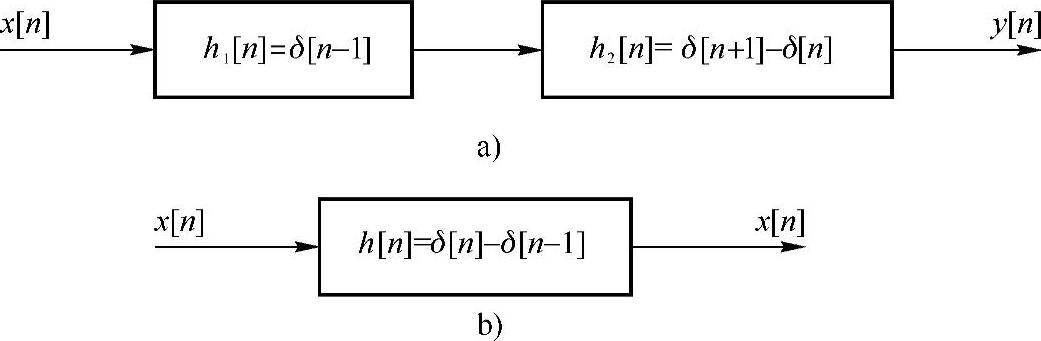
图1.4.5 非因果系统通过系统级联而成为因果系统

一般来说，任何非因果的有限冲激响应（Finite Impulse Response，FIR）系统只要与它级联一个足够长的延时系统，就可以构成一个因果系统。这就是数字系统优于模拟系统之处。

由系统的级联还可以得出一些关于可逆性有用的结论。如果系统是线性移不变的，且它的逆系统存在，而且也是线性移不变的，则这样两个系统的级联可以用来恢复输入信号，如图1.4.6a所示。设原系统的单位抽样响应为h[n]，其对应的逆系统（如果存在的话）单位抽样响应表示为h_inv[n]，则有

h[n]∗h_inv[n]=δ[n] （1.4.15）

系统如图1.4.6b所示。逆系统经常可以用来补偿系统的失真，但根据式（1.4.15）求h_inv[n]一般是困难的，有时只能进行逼近。

图1.4.6 逆系统对原系统的补偿作用