如何计算逆 z 变换：围线积分法

1.围线积分法

逆z变换是从复变函数X（z）求序列x[n]的过程，理论上的方法就是求复变函数的罗伦级数展开的过程。根据罗伦级数展开定理

式中

根据留数定理

根据留数的计算规则，如果z_k是一阶极点，那么

如果z_k是m阶极点，那么

按照此规则计算高级极点处的留数一般过程比较复杂。如果围线外没有高阶极点，则可以用变量替换来修正式（1.3.25），使计算n＜0时的留数得以简化，避免计算高阶极点留数的麻烦。为此可以令z=p^-1，代入式（1.3.25），则有

式中，围线取顺时针方向，而应用留数所取围线方向是逆时针方向。所以经变换方向后有

这一变量代换结果，相当于z平面的映像以倒置的形式映射到p平面。如果原先在z平面中的围线C的半径为r，则经映射在p平面中的围线C′是一个半径为1/r的圆；X（z）在围线外的极点映射为p平面围线C′内的极点。此外在原点或无限远外可能增加一些新的零点和极点，这是无关紧要的。这一变换使计算n＜0时的留数大为简化。

2.部分分式展开法

对于X（z）是有理分式这一类z变换，用部分分式展开求其逆z变换是方便的。设

则其部分分式展开为

式中，z_j为X（z）的一个r阶极点；各个z_k（k=1，2，…）是X（z）的单极点；B_n是X（z）的整式部分系数，当M≥N时，B_n存在，M=N时只有B₀项；M＜N时B_n=0。B_n的值可以用长除法获得。

展开式（1.3.31）的第二、第三项系数A_k、C_j，可以根据留数定理求得

或(www.xing528.com)

展开式各项确定以后，根据收敛域的不同，分别求出对应的逆z变换。原序列就是各个序列的和。

用部分分式求逆z变换，比较方便的方法是把X（z）转换成z的正幂次表示，然后按式（1.3.32）或式（1.3.34）的求解要求把X（z）表示成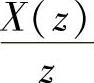（单极点情况）或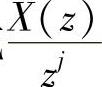（r阶重极点情况，j=1，2，…，r）形式，再按部分分式展开，求出各个系数。

3.幂级数展开法

求逆z变换也可以直接根据收敛条件把X（z）展开成幂级数形式，根据z变换的定义，对应z^-n项的系数即为x[n]。对于有理分式的情况，如果分母为1，则可以直接展开成幂级数形式；如果有极点，则可以通过长除法展开成幂级数，具体展开成正幂还是负幂级数取决于收敛域。

【例1.3.1】 给定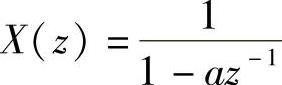，求分别在收敛域|z|＞|a|和|z|＞|a|内的x[n]。

解 收敛域为|z|＞|a|时，这是因果序列，用长除法展成负幂级数为

得到

所以有

x[n]=aⁿu[n]

收敛域为z＜a时，这是非因果序列，用长除法展成正幂级数为

得到

所以有

x[n]=-aⁿu[-n-1]

长除法的缺点是在比较复杂的情况下，难以得到x[n]的闭合表达式。