序列运算：重排和高级差分

序列x[n]作为自变量n的函数可以做各种运算，这些运算也是在信号处理中要经常遇到的处理方法。

1.序列相加

序列x₁[n]与x₂[n]相加，是指两个序列同序号的数值逐项相应相加，而构成一个新的序列y[n]，即

y[n]=x₁[n]+x₂[n] （1.2.18）

2.序列相乘

序列x₁[n]与x₂[n]相乘，是指两个序列同序号的数值逐项相应相乘，而构成一个新的序列y[n]，即

y[n]=x₁[n]·x₂[n] （1.2.19）

【例1.2.1】 设两个序列分别为

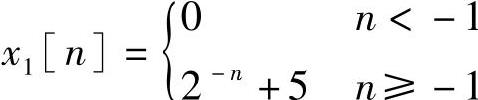和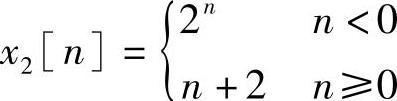

求x₁[n]+x₂[n]和x₁[n]·x₂[n]。

解

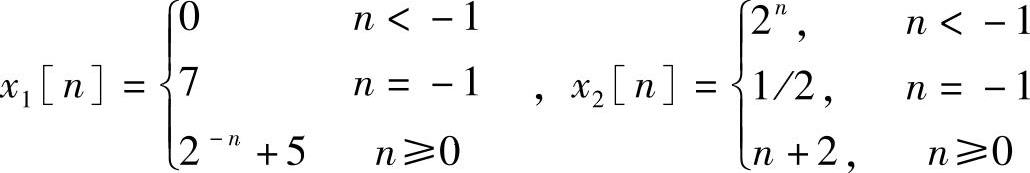
则

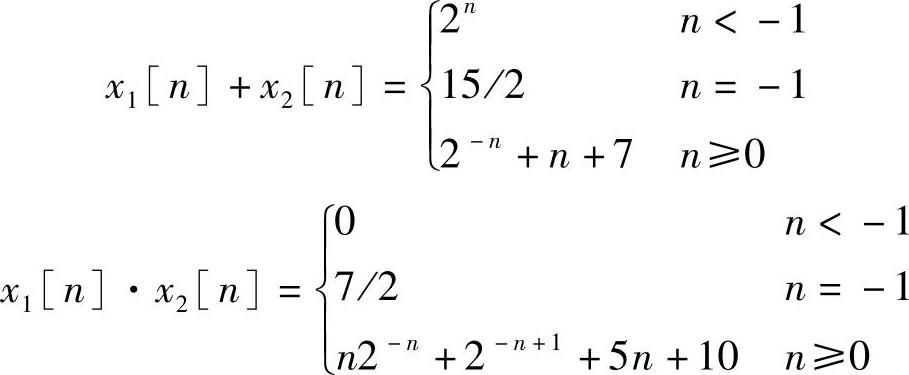
3.序列时延

序列时延是指原序列x[n]逐项依次向后移（右移）m位后，给出一个新序列

y[n]=x[n-m] （1.2.20）

若向前移（左移）m位为

y[n]=x[n+m] （1.2.21）

图1.2.9中分别描述了原序列（见图1.2.9a）、右移序列x[n-1]（见图1.2.9b）和左移序列x[n+1]（见图1.2.9c）的图形。

图1.2.9 序列的延时运算

4.序列反褶

序列反褶表示将自变量n换为-n，即

y[n]=x[-n] （1.2.22）

图1.2.10表示了反褶运算的过程，图1.2.10b表示对图1.2.10a序列的反褶。

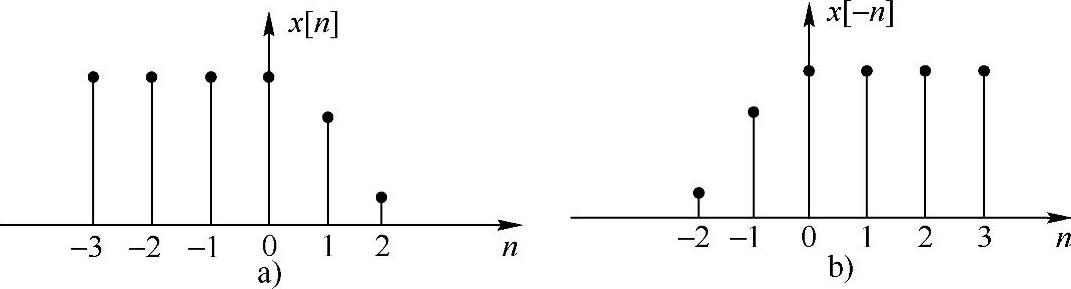
图1.2.10 序列的反褶

5.尺度变换

将波形压缩或扩展，这时要按规律去除某些点或补足相应的零点值，这种运算又称序列重排。

若将自变量n乘以整数M，则构成序列

y[n]=x[Mn] （M为整数） （1.2.23）

称为序列的压缩，也称为序列的抽取，它是把序列的某些值去除掉，余下的序列按次序重新排列。

序列的延伸正好与压缩变换相反，它是在原序列两相邻值之间插入零值，所以也称为序列内插零值。其表示式为

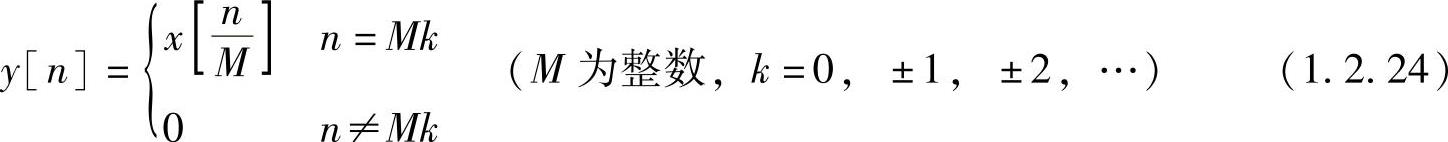
【例1.2.2】 已知序列x[n]如图1.2.11a所示，请画出x[2n]和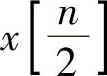的波形。

解 依题意序列x[n]以整数倍2抽取的序列x[2n]和以整数倍2内插的序列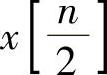的波形分别如图1.2.11b所示。

6.序列差分（对应于连续信号的微分）

在离散时间信号中的差分运算是指同一序列中相邻序号的两个序列幅度之差，按所取序号次序不同可以分为前向差分和后向差分。

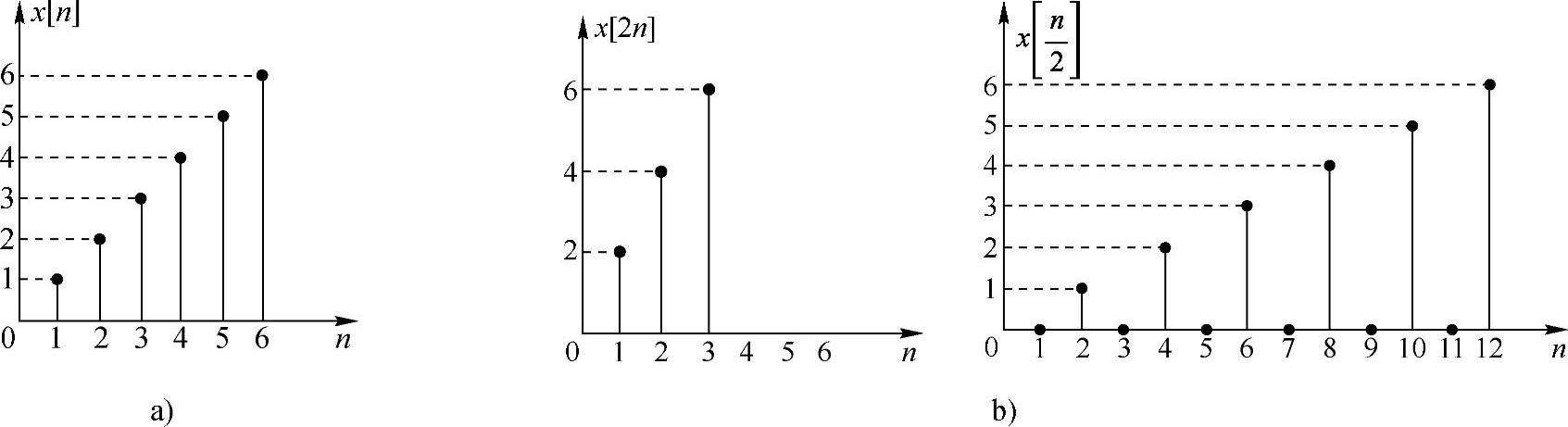
图1.2.11 例1.2.2图

前向差分表示为

Δx[n]=x[n+1]-x[n] （1.2.25）

后向差分表示为

▽x[n]=x[n]-x[n-1] （1.2.26）

式中，Δ和▽分别为前向差分和后向差分运算符号。

如果对序列x[n]进行多次差分运算，就成为高级差分，表示为

▽^mx[n]=▽（▽^m-1x[n]） （1.2.27）

式（1.2.27）表示对序列x[n]做m次后向差分运算。

例如二阶前向差分(www.xing528.com)

Δ（Δx[n]）=Δ²x[n]=Δx[n+1]-Δx[n]

=x[n+2]-2x[n+1]+x[n] （1.2.28）

二阶后向差分

▽（▽x[n]）=▽²x[n]=▽x[n]-▽x[n-1]

=x[n]-2x[n-1]+x[n-2] （1.2.29）

7.序列的求和（对应于连续信号的积分）

求和（累加）运算定义为

它表示序列y[n]在时刻n的值等于x[n]当前时刻n的值和x[n]以前所有值的总和。比如x[n]的值如图1.2.12a所示，则求和值y[n]如图1.2.12b所示。

8.序列的能量

序列的能量定义为序列各抽样值的二次方和，即

9.序列的卷积和

在连续时间线性时不变系统中，卷积积分是求零状态响应的主要方法。在离散时间系统分析中卷积和同样也是求线性移不变系统零状态响应的主要方法。

设两个序列x[n]和h[n]的卷积和定义为

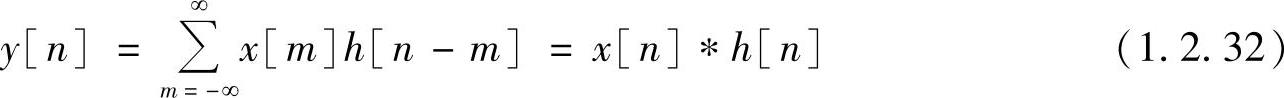
式中，“*”表示两个序列做卷积运算。

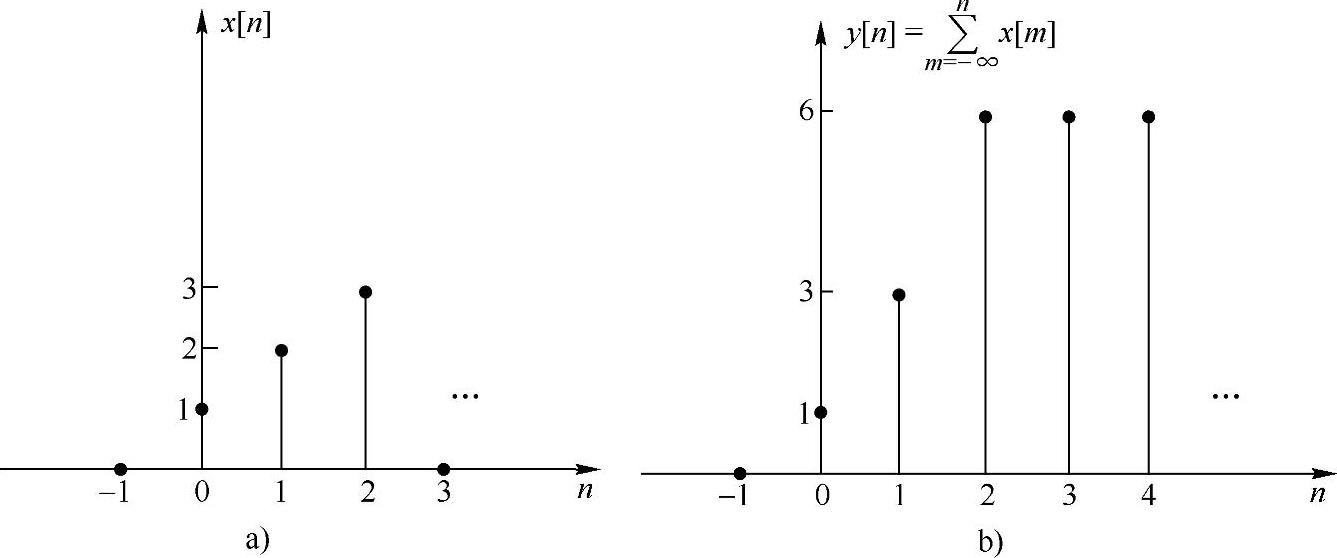
图1.2.12 序列求和运算

卷积运算的求解过程可以通过如下步骤进行：

第一步：换坐标，把x[n]和h[n]用x[m]和h[m]表示。

第二步：将其中一个序列加以反褶，比如h[m]进行反褶，形成h[-m]。

第三步：将反褶后的序列移位n，表示成h[n-m]。当n＞0时，序列右移；当n＜0时，序列左移。

第四步：将x[m]和h[n-m]相同m的序列值对应相乘后，再相加，即得到卷积结果y[n]。

【例1.2.3】 设x[n]=R₄[n]，h[n]=R₄[n]，求y[n]=x[n]∗h[n]。

解

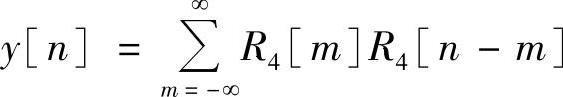
上式中矩形序列长度为4，求解上式主要根据矩形序列的非零值区间确定求和的上、下限，R₄[m]的非零值区间为0≤m≤3，R₄[n-m]的非零值区间为0≤n-m≤3，其乘积值的非零值区间，要求m同时满足下面两个不等式

0≤m≤3

n-3≤m≤n

因此

当0≤n≤3时，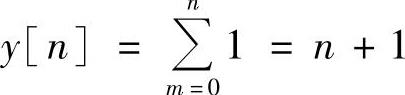

当4≤n≤6时，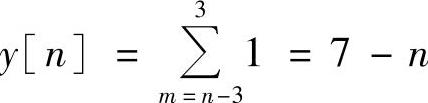

卷积过程以及y[n]波形如图1.2.13所示，用公式表示为

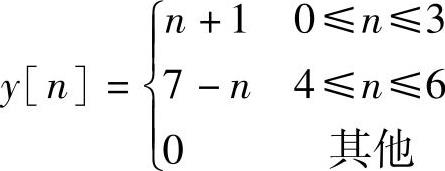
对两个有限长序列，例如序列x[n]的长度为N点，h[n]的长度为M点，则y[n]=x[n]∗h[n]结果序列的长度为N+M-1点。

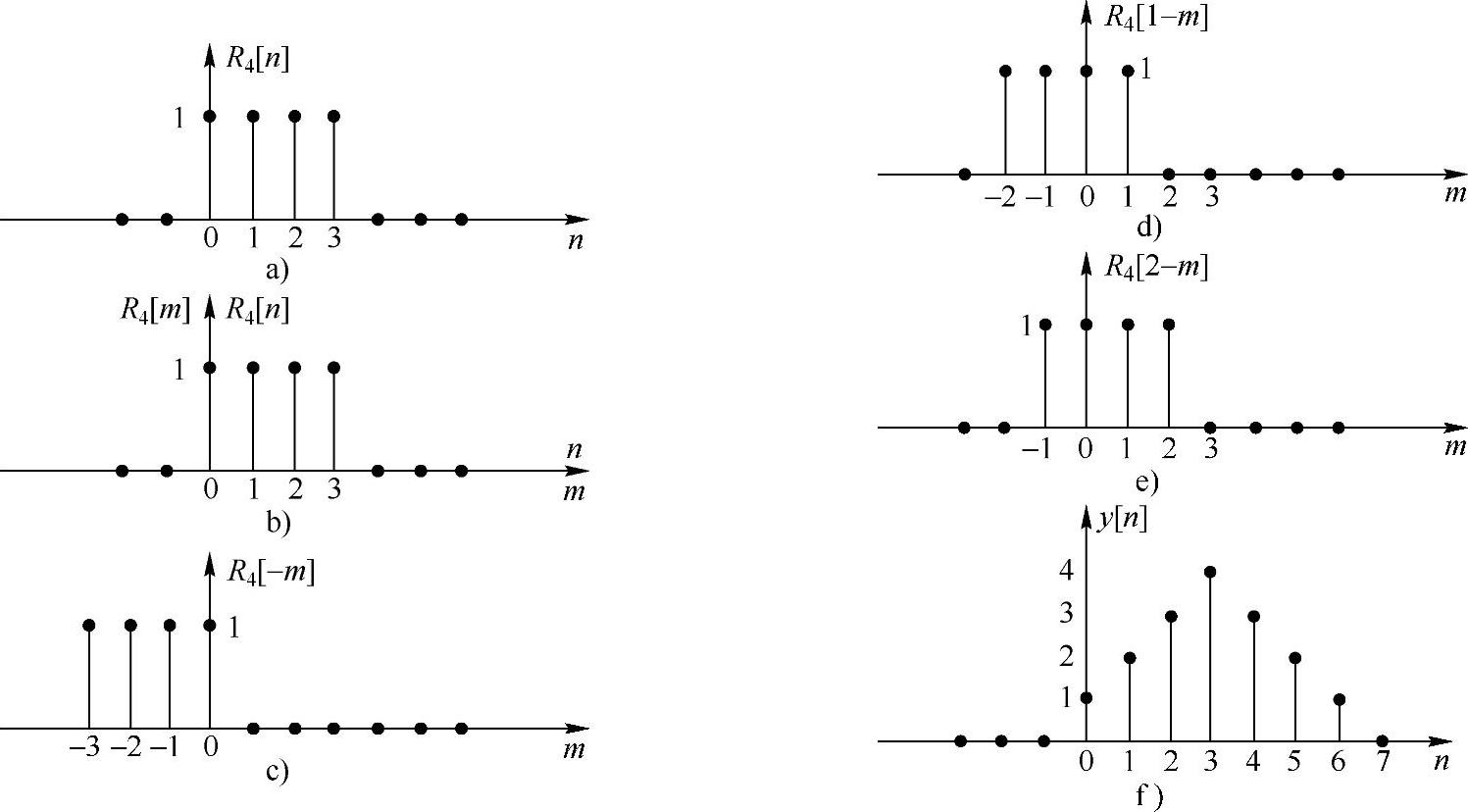
图1.2.13 x[n]和h[n]卷积和的图形运算

10.两序列的相关运算

设两个序列x[n]和y[n]的相关运算定义为

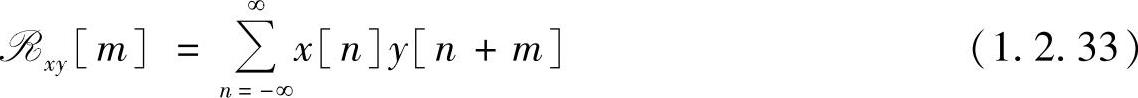
从式（1.2.33）可以看出，相关运算是一个序列相对于另一个序列进行位移，然后相乘求和。它与序列卷积运算是相似的，但没有像卷积运算中有反褶的过程。于是可以用卷积符号“*”来表示相关运算，即有

R_xy[m]=x[m]∗y[-m] （1.2.34）

在信号分析中往往用到自相关序列，令式（1.2.33）中的y[n]=x[n]，则有自相关序列

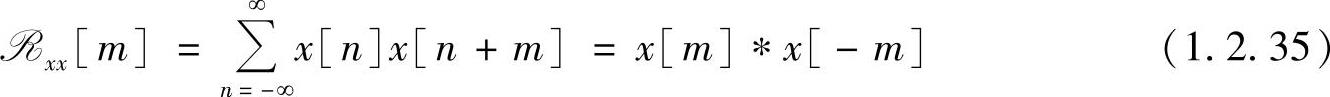
自相关序列的一个重要特性是，自相关序列是偶对称序列，即

在式（1.2.35）中，当m=0时，即为序列的能量，此时