基本序列：单位抽样、单位冲激、矩形、实指数、周期正弦、余弦

在讨论离散时间信号与系统理论时，有几个基本序列是特别重要的，下面分别予以讨论。

1.单位抽样序列δ[n]

δ[n]类似于连续时间信号中的单位冲激信号δ[t]，因而也称为单位冲激序列，它们的作用是相同的，所不同的是，δ[t]是广义函数，在t=0时刻幅度趋向于无穷大，即无幅度可言，只有用面积表示的强度。而δ[n]在n=0时刻有确定的幅度值，就是1。单位抽样序列和单位冲激信号如图1.2.2所示。

图1.2.2 单位抽样序列和单位冲激信号

a）单位抽样序列 b）单位冲激信号

一般情况下，任何序列都可以表示为

在离散时间线性系统分析中，将会用到式（1.2.4）。

2.单位阶跃序列u[n]

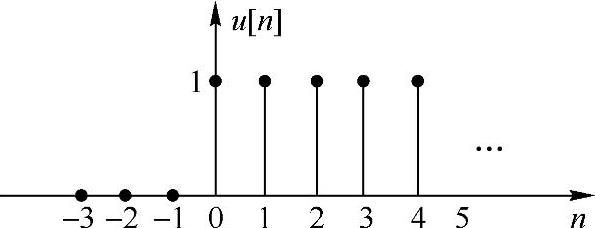
图1.2.3 单位阶跃序列

单位阶跃序列如图1.2.3所示。它类似于连续时间信号中的单位阶跃信号u（t），它是一个右边序列，经常和其他序列相乘，组成一个因果序列。δ[n]与u[n]之间的关系为

或者

3.矩形序列R_N[n]

式中，N称为矩形序列的长度，其波形如图1.2.4所示。如果用单位阶跃序列来表示矩形序列，则有

R_N[n]=u[n]-u[n-N] （1.2.10）

4.实指数序列aⁿu[n]

x[n]=aⁿu[n] （1.2.11）

这是单边指数序列，其中|a|为实数。当a＜1时，序列是收敛的；当|a|＞1时，则序列是发散的。图1.2.5是0＜a＜1时aⁿu[n]的波形。

图1.2.4 矩形序列

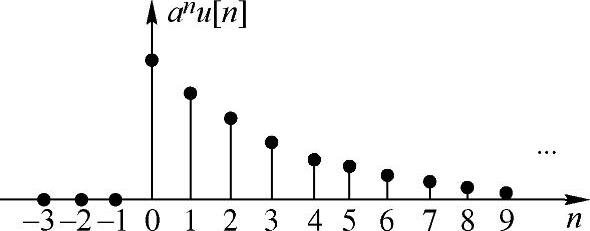
图1.2.5 实指数序列（0＜a＜1）

5.周期序列

若对所有n存在一个最小的正整数N，满足(www.xing528.com)

x[n]=x[n+N] （-∞＜n＜∞） （1.2.12）

则称此序列为周期序列，其周期为N。图1.2.6表示以N=6为周期的3点矩形周期序列。

6.正弦序列

正弦序列也是一个非常重要的序列，它的一般形式可表示为

x[n]=Acos（ω₀n+φ） （1.2.13）

式中，A是幅度；φ是初始相位；ω₀是数字角频率，单位是弧度，它表示序列变化的速率，或者说表示相邻两个序列值之间变化的弧度数。

图1.2.6 周期序列

连续的正弦信号是周期性信号，但正弦序列不一定是周期序列，只有满足某些条件时，才是周期序列。

由于

x[n]=x[n+N]=Acos[ω₀（n+N）+φ）=Acos[ω₀n+ω₀N+φ] （1.2.14）

若

ω₀N=2πk （k为整数） （1.2.15）

则有

Acos[ω₀（n+N）+φ）=Acos[ω₀n+φ]

此时正弦序列是周期序列，且周期为

当k=1时，N=2π/ω₀为最小正整数，此时正弦序列是以N为周期的正弦序列。图1.2.7表示周期N=12的余弦序列。

若，此时要使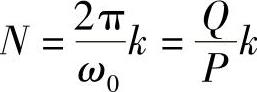为最小整数，只有k=P，所以周期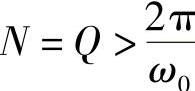。图1.2.8表示了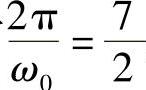周期N=7时的正弦序列。

图1.2.7 周期性余弦序列

图1.2.8 周期性正弦序列（N=7）

若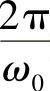为一无理数，则任何k值都不能满足N为正整数，此时正弦序列就不可能是周期性序列。

不管正弦序列是否是周期性序列，统称ω₀为正弦序列的角频率，而且其主值范围规定在-π≤ω₀≤π或0≤ω₀≤2π区间内，这是因为正弦序列作为ω₀的函数，是以2π为周期的周期性函数。

7.复指数序列

复指数序列表示为

当σ=0时，复指数序列和正弦序列一样，只有当2π/ω₀为整数或有理数时，才是周期性序列。

复指数序列e^jωn和连续时间信号的复指数信号e^jωt一样，在信号分析中扮演重要角色，是序列进行傅里叶变换时所用的，作为完备正交函数集。