LC正弦波振荡电路设计优化

LC振荡电路用来产生高频正弦信号，一般由放大器、选频网络和反馈电路三部分组成。振荡电路可分为变压器耦合式振荡器和三点式振荡器两大类。

1.LC并联谐振回路的选频特性

LC和RC振荡电路产生正弦波振荡的原理与结构相似，LC振荡器也有放大电路、正反馈网络、选频网络和稳幅环节。只是其选频网络是LC谐振电路，并且工程中LC谐振电路有串联和并联两种形式。这里介绍的LC振荡器采用LC并联谐振回路。先简要复习电路课程中LC并联谐振回路的选频特性。

图9-7 并联谐振回路及其谐振曲线

a）LC并联谐振回路 b）并联谐振曲线 c）考虑电路损耗的LC并联谐振回路

图9-7a所示电路发生谐振时

由此解得谐振频率为

如果考虑电感线圈的损耗，则用电阻R表示线圈损耗，见图9-7c。可得到并联谐振回路的导纳为

LC并联谐振回路产生谐振时，上式的虚部为零，即

则谐振角频率ω₀为

式中，Q为并联谐振回路的品质因数

品质因数Q是谐振回路的主要品质指标，其典型值为几十至数百。Q值越大，谐振回路的选频性能越好。例如，对于图9-7b的谐振曲线，图中Q₁＞Q₂，Q值大的曲线较陡峭，因而谐振回路的选频性能更好，抑制干扰的能力越强。

当Q＞＞1时，，则谐振频率f₀的表达式和式（9-14）相同。将ω₀代入式（9-15）可得

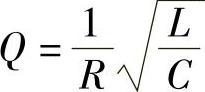
上式表明，相同谐振频率下，选频网络的损耗越小，电容容量越小，电感数值越大，LC并联谐振回路的品质因数就越大，则谐振回路的选频性能越好。

LC并联谐振回路产生谐振时，ω=ω₀，则谐振回路的等效电抗为

当Q＞＞1时，Z₀=RQ²

2.变压器耦合式LC正弦波振荡器

变压器耦合式LC振荡器如图9-8a所示，BJT组成分压式偏置稳定共射放大电路，电路具有合适的静态工作点且工作在放大状态。LC并联谐振回路作为BJT的集电极负载，反馈线圈L₂与电感线圈L耦合，将反馈信号送到共射放大电路的输入端。

图9-8 变压器耦合式LC振荡电路

a）振荡电路 b）同名端的极性标注

根据瞬时极性法可判断电路是否满足自激振荡的相位平衡条件：将图9-8的反馈支路（L₂到电容C_B的线路）断开，在放大电路的输入端加入频率为f₀的电压信号，假设其极性瞬时为正，用（+）表示。由于LC并联回路谐振时为纯电阻性，故BJT的集电极和基极的电位相位差为180°，即BJT的集电极和基极的电位极性相反，所以BJT的基极电位极性为（+）而集电极电位极性为（-）。根据变压器绕组间“同名端同极性”（图9-8b）的标注原则，线圈L₂的电压为上“正”下“负”。可见，线圈L₂上的反馈电压与的极性相同，电路引入正反馈，所以放大电路满足自激振荡的相位平衡条件。

从自激振荡的幅值平衡条件看，只要合理选择变压器一次、二次侧线圈的匝数比和电路其他电路参数，电路很容易满足幅值平衡条件。

变压器耦合式LC振荡器的振荡频率f₀表达式与式（9-14）相同。(www.xing528.com)

变压器耦合式LC振荡器的优点是易于起振，输出电压的波形失真较小；缺点是磁路耦合不紧密，损耗较大，振荡频率的稳定性不高。

3.LC三点式正弦波振荡器

（1）电感三点式LC振荡电路

图9-9为电感三点式LC振荡电路（基本放大电路为共基组态）。电感线圈L₁和L₂是一个线圈，②点是中间抽头。因为图中反馈回路的三个端点分别接到BJT的三个电极，故取名为三点式振荡器。如果设某个瞬间集电极电流减小，线圈上的瞬时极性如图所示。反馈到发射极的极性对地为正。图中晶体管是共基极接法，所以使发射结的净输入减小，集电极电流减小，符合正反馈条件。若L₁、L₂之间的互感为M，且品质因素Q远大于1时，则以上两种电路的振荡频率均为

图9-9 电感三点式LC振荡电路（基放CB）

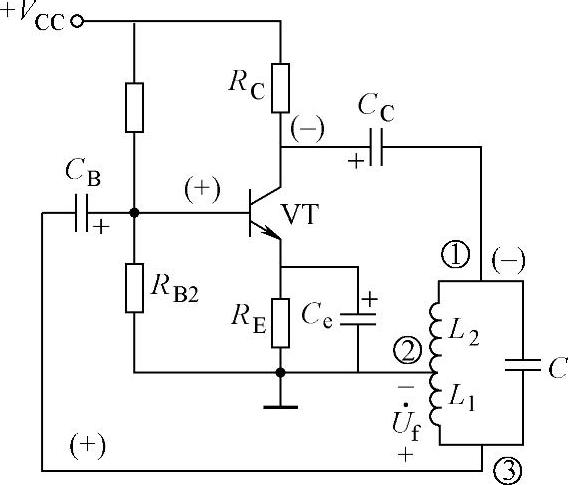
图9-10 电感三点式LC振荡电路（基放CE）

这两种振荡电路的工作频率范围可从数百千赫到数十兆赫。以上电路的特点是：L₁、L₂之间有互感，耦合紧密，反馈较强，容易起振，振幅大。调整电容C的大小，可获得调节范围较宽的振荡频率，而且C的改变基本上不影响电路的反馈系数，但此类电路振荡波形不好，故振荡频率不能做得太高。

（2）电容三点式LC振荡电路

电容三点式LC振荡器也有两种常用的电路，如图9-11所示。

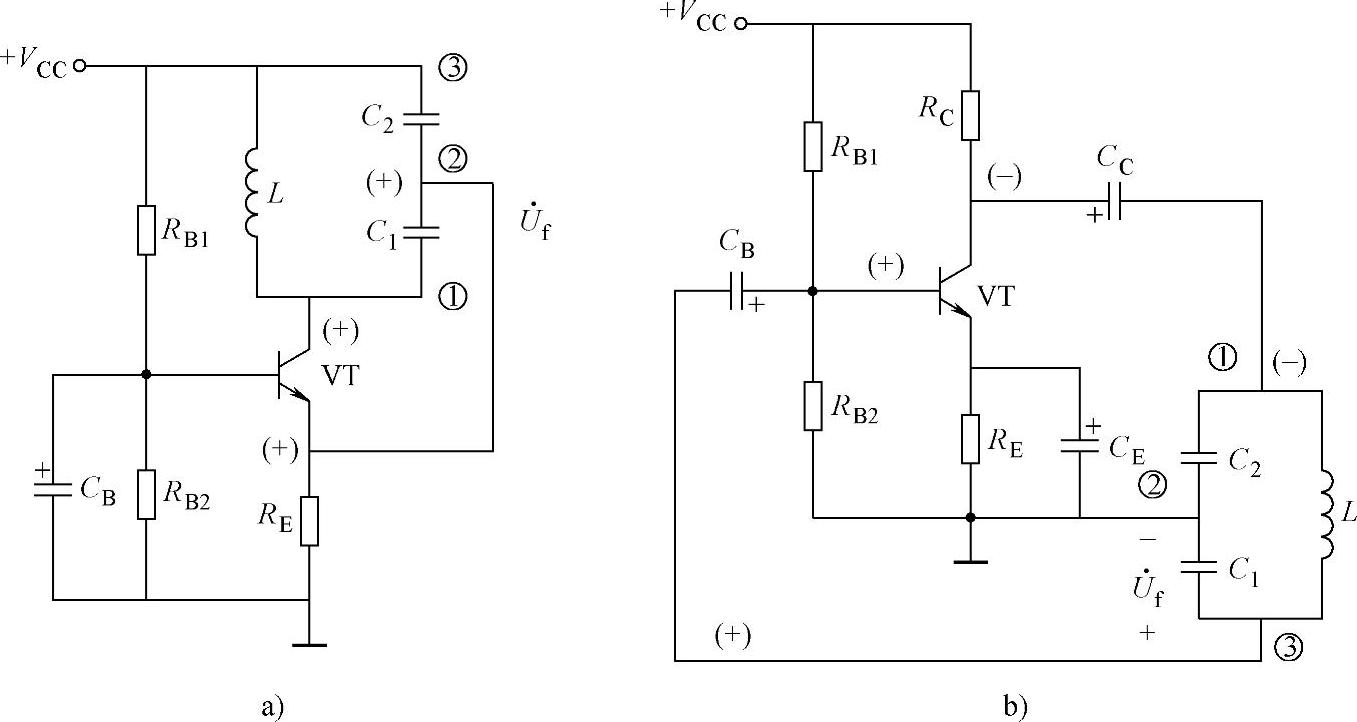
图9-11 电容三点式LC振荡电路

a）共基组态 b）共射组态

利用瞬时极性法可判断出此两电路均为正反馈（图上标注了瞬时电位极性），故满足了相位条件。

当由L、C₁和C₂所构成的选频网络的品质因素Q远大于1时，电容三点式LC振荡器的振荡频率估算式为

这种电路的特点是，振荡波形好，频率稳定度较高，工作频率可以做得较高，但调整C₁或C₂来改变振荡频率时，反馈系数也将改变。

【例9-3】判断图9-12中两个电路能否振荡，如能振荡，估计其振荡频率。已知两个电路中L=0.4mH，C₁=C₂=25pF。

图9-12 例9-3图

解：图9-12a所示电路不能振荡。

图中共射放大器是基本放大器部分，同时具有选频功能，电容C₁、C₂构成反馈网络。但当LC并联谐振回路谐振时，φ_A=180°，又知，φ_F=0°，从而有φ_A+φ_F=180°，不满足振荡的相位条件。

图9-12b所示电路能振荡。

本电路属于电容三点式LC振荡器。选频放大器是共基极组态，LC并联谐振回路谐振时φ_A=0°，又知，φ_F=0°，从而有φ_A+φ_F=0°，满足振荡的相位条件。振荡频率

图9-13 例9-4的振荡电路

【例9-4】图9-13是集成运放构成的LC振荡电路，试判断它们能否产生正弦波振荡。

解：图9-13a和图9-13b中反馈回路①、②、③三个端点分别接到集成运放的两个输入端和一个输出端，故两图电路均为三点式振荡电路。

通过以上电感三点式和电容三点式LC振荡电路的学习，可以总结组成三点式LC振荡电路的一些规律。由BJT组成放大电路的三点式LC振荡电路，与BJT发射极相连的电抗是同性质的电抗。如图9-9和图9-10所示，与BJT发射极相连的电抗是电感L₁和L₂；如图9-11所示，与BJT发射极相连的电抗是电容C₁和C₂。由集成运放组成放大电路的三点式LC振荡电路，与集成运放同相输入端相连的电抗是同性质的电抗，如图9-13所示。