模拟乘法器在运算电路中的优化应用方案

利用模拟乘法器与其他器件相组合，通过各种不同的外接电路，可实现各种运算电路，还可组成函数发生器，调制和解调电路等。下面介绍几种基本应用。

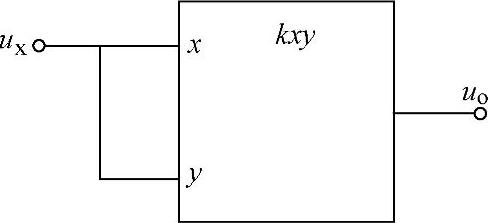
图7-29 平方运算电路

1.平方运算电路

利用四象限模拟乘法器能够实现平方运算，如图7-29所示，将模拟乘法器两个输入端并联在一起后接上输入电压u_i，即可组成平方运算电路。

输出电压为

u_o=ku²_i （7-55）

如果输入信号为正弦波时，则

输出电压u_o中含有输入信号u_i的2倍频交流电压信号，为了得到纯交流电压信号，可在输出端加耦合电容，以隔断直流分量。

2.平方根运算电路

将平方运算电路接在集成运放的反馈回路中，可以构成反函数型的平方根运算电路，如图7-30所示。

根据“虚地”和“虚断”的概念，可得

所以，输出电压为

(www.xing528.com)

由式（7-56）可知，模拟乘法器的k＞0，则u_i＜0，即输入电压u_i必须为负值。如果因某种原因使u_i＞0，从而使反馈极性为正，最终使集成运放电路内部的晶体管工作在截止区或饱和区，输出电压接近电源电压，以至于即使u_i变得小于零，晶体管也不能回到放大区，电路不能恢复正常工作，集成运放出现闭锁（或称锁定）现象。为了解决这个问题，常在输出回路中接一个二极管和一个电阻R_L，如图7-31所示。

图7-30 平方根运算电路

图7-31 防止锁定的平方根运算电路

为使u_i＞0时平方根运算电路也能工作，在乘法器输出电压u_o1经一反相器再加到集成运放的输入端。

3.除法运算电路

图7-32为除法运算电路，图中模拟乘法器的接入必须使集成运放的外部电路引入负反馈，这样电路才能正常工作。如图7-32所示，必须保证i₁=i₂时，电路引入的反馈才是负反馈。由于u_o和u_i1反相，故要求u_o与u_o1同极性。因此，当采用同相模拟乘法器时，u_i2应该大于零；而当采用反相模拟乘法器时，u_i2应该小于零。

根据“虚地”和“虚断”的概念，i₁=i₂，即

得输出电压为

在图7-32所示的除法电路中，u_i2必须小于零，即这样的除法器是两象限的。

图7-32 除法运算电路