1.晶体管的高频等效模型及其简化
图5-4a为晶体管结构示意图及混合参数π等效模型。
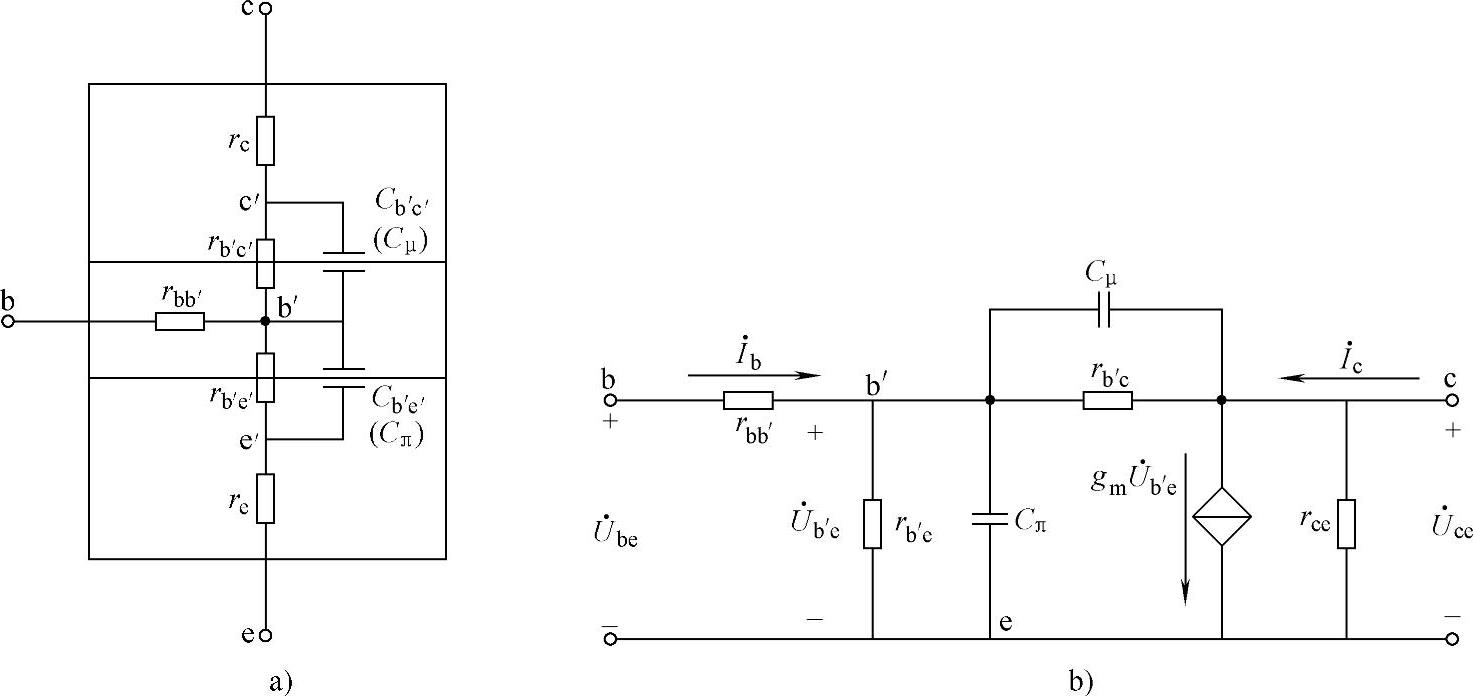
图5-4 晶体管结构示意图及混合参数π等效模型
a)晶体管结构示意图 b)混合参数π等效模型
Cμ为集电结的结电容,约几十到几百皮法;Cπ为发射结的结电容,约几个皮法;rb′c′为集电结的结电阻,rb′e′为发射结的结电阻,rbb′为基区体电阻。re为发射区体电阻,由于发射区掺杂浓度高,re数值较小,常忽略不计。rc为集电区体电阻,数值比与其串联的rb′c′小得多,也忽略不计,则rb′c≈rb′c′,rb′e≈rb′e′。结电阻rbe分为基区体电阻rbb′和发射结动态电阻rb′e两部分,即rbe=rbb′+rb′e。图5-4b为晶体管的混合参数π等效模型,简称混合π模型。
一般情况下,rce远大于集电极与发射极之间所接的负载电阻,rb′c也远大于Cμ的容抗,因此rce和rb′c可视为开路。简化后的混合参数π等效模型如图5-5所示。
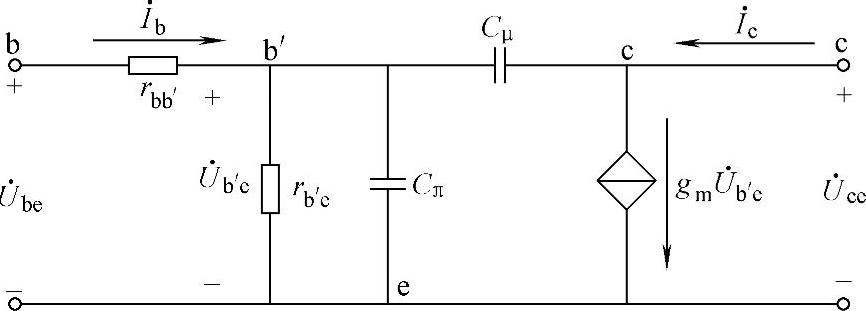
图5-5 简化的混合π模型
受结电容影响,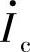 与
与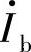 比值的大小、相位均与频率有关,
比值的大小、相位均与频率有关,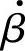 为频率的函数,而
为频率的函数,而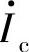 与
与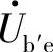 有线性关系,因此引入参数gm,用
有线性关系,因此引入参数gm,用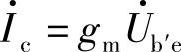 描述
描述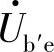 对
对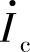 的控制关系。gm称为跨导,量纲为电导,它是一个常数,定义为
的控制关系。gm称为跨导,量纲为电导,它是一个常数,定义为

简化的混合h参数等效模型与简化后的混合π模型电阻和受控源的物理意义是相同的,因而参数大小也相等。则
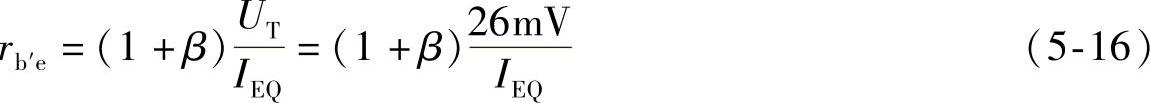
且

式中,β0为低频段晶体管的电流放大系数。由式(5-17)得
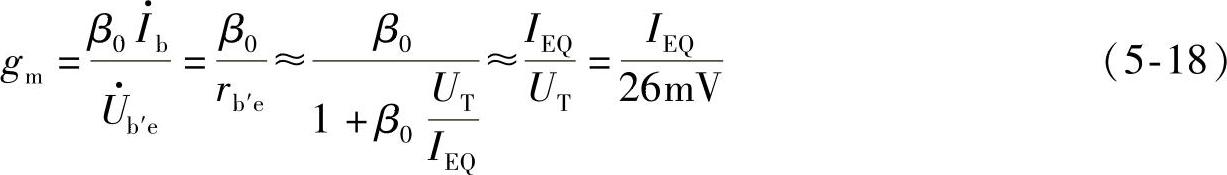
Cob是晶体管为共射接法且发射极开路时C—B之间的结电容,可由手册查得,近似计算时Cμ可用Cob近似。Cπ的值往往需要通过计算得到。
2.晶体管共射电流放大系数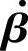 的频率响应
的频率响应
由图5-5所示混合π模型可知,当输入信号频率处于低频段或者中频段时,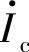 与
与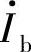 的比值为常数,与频率无关。当输入信号处于高频段时,
的比值为常数,与频率无关。当输入信号处于高频段时,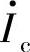 与
与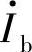 的比值随频率发生变化,即
的比值随频率发生变化,即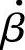 是频率的函数。
是频率的函数。
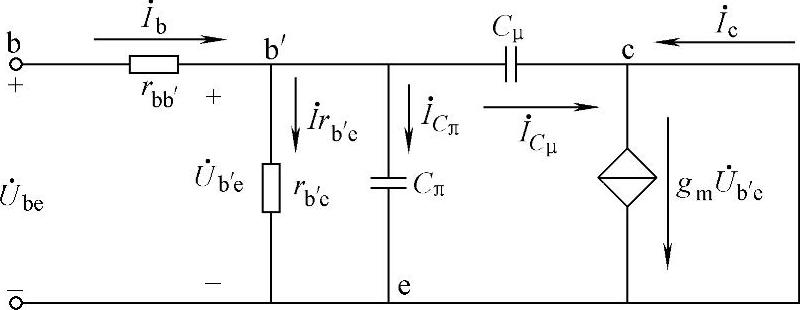
图5-6 分析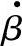 频响的等效电路
频响的等效电路
根据共射电流放大系数的定义,有
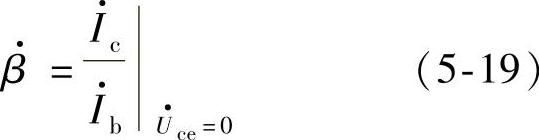
根据式(5-19),将c、e之间短路,得如图5-6所示电路。
在图5-6中
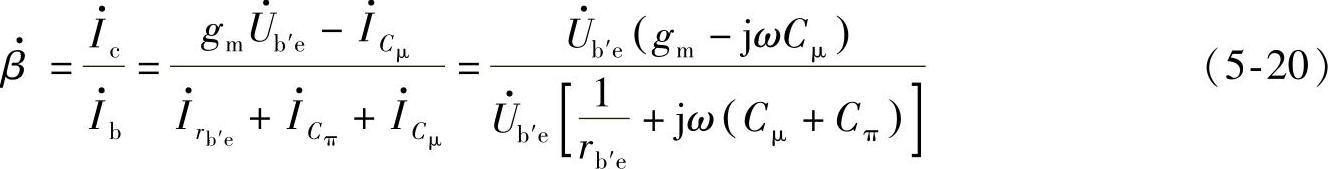
在混合π模型有效范围内,gm>>ωCμ,则
 (https://www.xing528.com)
(https://www.xing528.com)
由式(5-18),β0=gmrb′e,得
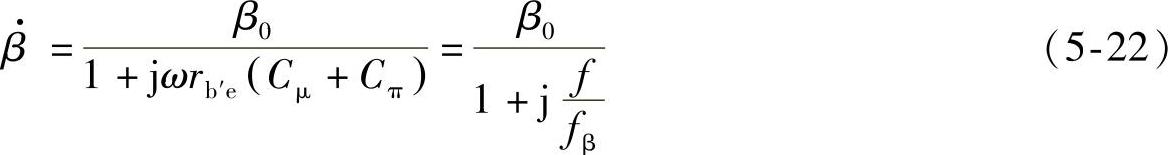
上式与式(5-12)形式一样,所以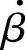 的响应与低通电路相似,fβ称为
的响应与低通电路相似,fβ称为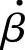 的截止频率。
的截止频率。

一般情况下,Cπ>>Cμ,则

可求得Cπ

由式(5-22)写出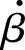 的频率响应特性
的频率响应特性
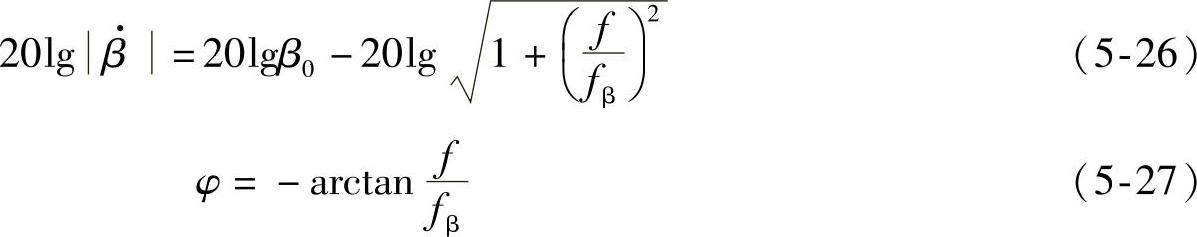
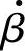 的波特图如图5-7所示。
的波特图如图5-7所示。
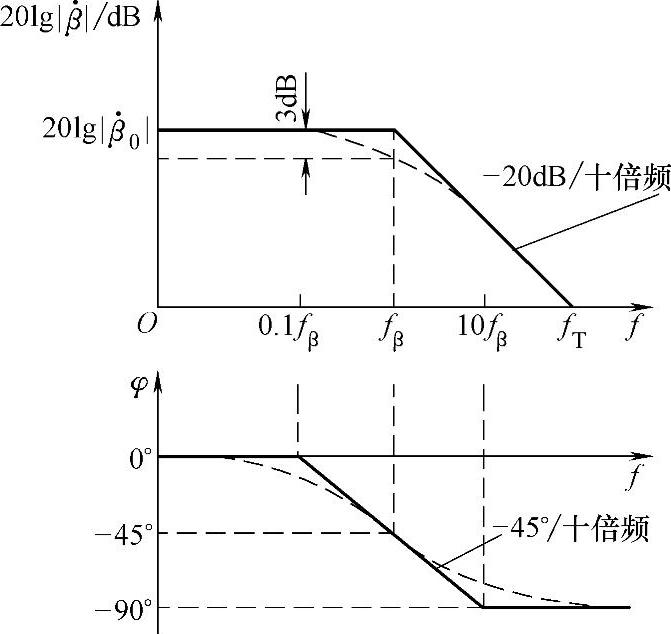
图5-7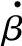 的波特图
的波特图
如图5-7所示,fT是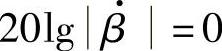 时的频率,称为BJT的特征频率,f=fT时,
时的频率,称为BJT的特征频率,f=fT时,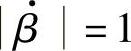 。
。
在式(5-26)中,令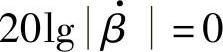 ,则f=fT,可
,则f=fT,可
得
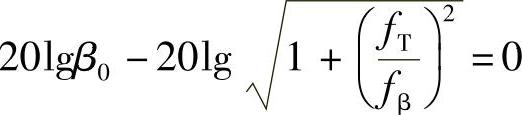
则
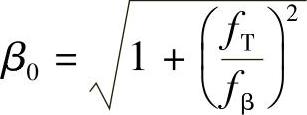
由图5-7可知,fT>>fβ,所以有
fT≈β0fβ (5-28)
将上式代入式(5-24),得

根据式(5-29),Cπ又可用fT表示

根据元件手册中查出的fβ或者fT,运用式(5-25)和式(5-30),可以计算出Cπ的值。
为了方便计算晶体管的高频等效模型参数,式(5-31)归纳了相关参数的计算公式。
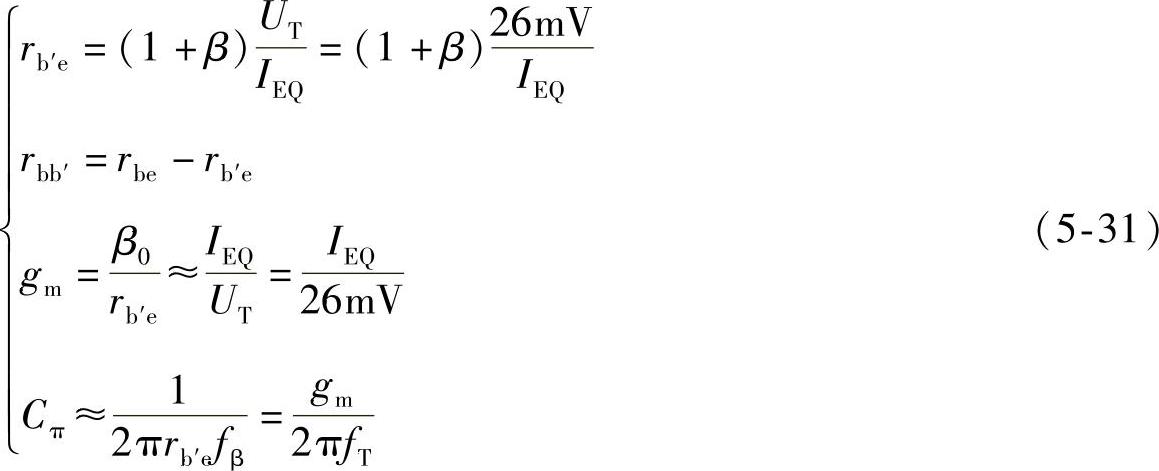
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




