使用非晶态铁氧体设计磁开关，以宽高比与包扎因子为参考

1.磁心材料

软磁材料如硅钢、铁镍合金等传统材料大都是液态金属以10^-5～10³K／s的冷却速度在平衡或平衡凝固条件下得到的。1970年前后，材料的快速冷凝技术获得重大突破。用冷却速度高达10⁸K／s的快速冷凝技术可以得到平衡或亚平衡凝固条件下不可能得到的亚稳态材料——非晶（Amorphous）、纳米晶（Microcrystallites，也称微晶）材料。由于非晶、纳米晶材料的磁晶各向异性近似为零，因此它具有一般磁晶体所没有的、独特的软磁特性。而且非晶材料的制备工艺是将液态金属快淬成薄带，省去了锻造、热轧、冷轧等工序，有利于节约能源，提高材料的成材率。近年来，非晶和纳米晶材料得到了迅速的发展，成为不可替代的软磁材料，它可通过快淬、真空蒸镀、化学沉积、电沉积以及等离子体溅射等方法制成。它与晶态合金材料相比有许多优点。如电阻率较高，可达120～270×10^-6Ω·cm；矫顽力较小，经过磁场热处理的H_c可达数个1／（4π）A／m；此外，还具有强度高、韧性好、耐磨、耐腐蚀等特点，且通过材料成分、工艺等调节，还可控制或改变磁滞回线的形状，以适应各种场合的需要。这类材料可用作磁头、磁屏蔽、变压器、转换器、传感器、漏电保护、磁开关、脉冲变压器以及其他磁性元件。非晶磁性材料的不足之处是起始磁导率低和居里温度不高，而且由于是处于亚稳态，故稳定性也是个问题。非晶磁性材料有铁基材料、铁镍基材料与钴基材料之分。3种磁性材料中钴基合金材料的磁导率高，故功耗较小，而且它的初始非饱和磁通较小，故响应速度快，宜于做磁开关和仪表磁性元件。但其最大磁感应强度较小，故用它做磁开关，磁心体积较铁基和铁镍基非晶态材料大，但响应速度较两者快。图5-10所示，是以上3种非晶磁性材料部分牌号热磁补偿合金的B-T曲线。

图5-10 一些热磁补偿合金的B-T曲线

非晶态合金、纳米晶合金、磁粉心金属氧化物等磁心材料，与硅钢磁心材料相比，铁损非常小，这一特性引起人们的极大重视。早在1960年，波尔帕威兹（PolPuwez）用大约10℃／s的淬火速度研制出来。1973年，美国的阿拉德公司，以麦特格拉斯（Metglass）的名字制出了成品。它与硅钢相比，其铁损曲线如图5-11所示。不过非晶态材料中铁基的最便宜，尤以非晶态铁氧体为最，而钴基非晶态合金磁价格则十分昂贵，故在此项研究中，更倾向于使用廉价的非晶态铁氧体做磁开关，但脉冲变压器经常采用非晶态合金磁心来设计绕制。

图5-11 铁损曲线

磁开关的磁心选择原则：高频特性好，且高频损耗小；初始磁导率高；磁感应强度变化量ΔB（＝B_r＋B_s）大（B_r为剩余磁感应强度，B_s为饱和磁感应强度），但B_r又不能太大，否则磁复位困难；电阻率高，即磁滞回线越窄越高越好。

脉冲变压器与磁开关的设计方法一样，除了与磁性材料的选择有关，还与其磁路的设计有关，但磁性材料的性能参数决定了磁路的计算与设计，它主要考虑磁介质物质的磁化曲线、磁导率、气隙磁导、漏磁、涡流与涡流损耗、磁滞损耗、集肤效应等，然后根据磁路的计算模型，形成电压、电流、脉宽、磁路、损耗、频响的模型，从而为脉冲功率系统电路建模打下基础。

2.磁开关磁心体积与结构的确定

磁开关所要求的磁心体积由下式给出：

式中，μ_sat为饱和磁导率；E_s为磁开关的能量；G为磁开关的增益（与磁开关压缩比成正比）。

由此可见，磁开关的磁心体积与绕线匝数和磁心的高宽比无关，也就是说，我们在设计磁开关时，对于磁心的高宽比有较大的选择范围，而不必考虑会导致要求增加磁心体积。但在实际应用中，因为高宽比不同，对于磁开关绕线截面积是有影响的，所以这也会影响到磁心体积的选择。

典型环形磁心的截面积如图5-12所示，该磁心为环形结构，其厚度和高度分别为Δr和h。磁心与绕线间的间隙为X／2。该磁开关的饱和电感是

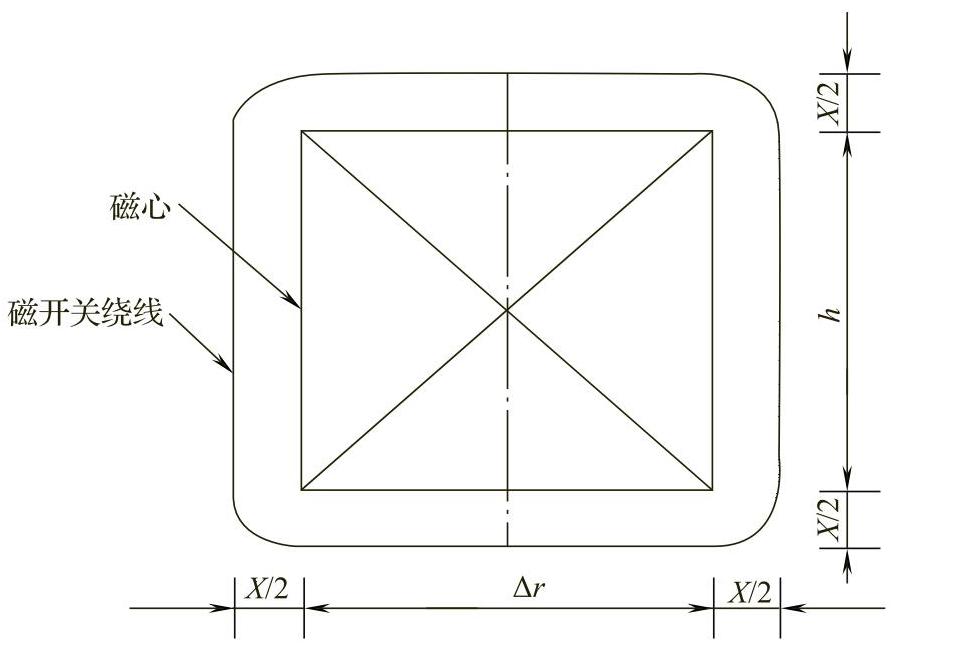
图5-12 环形磁开关截面积视图

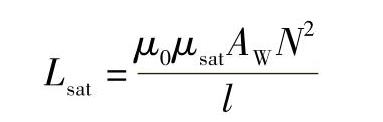
式中，μ₀、μ_sat分别为初始磁导率和磁心饱和相对磁导率；A_W为绕线封闭的截面积；N为绕线匝数；l为磁心的平均磁路长，l＝U_c／A_c，U_c为磁心体积，A_c为磁心截面积。

磁开关的包扎因子可定义为

则

或者

假设通过磁开关两端的电压波形为

U_L(t)＝U₀(1-cosωt)

则由法拉第定律得到

式中，α为磁心的叠层因子；t_sat为磁开关饱和时间。

所以

将上式代入得到

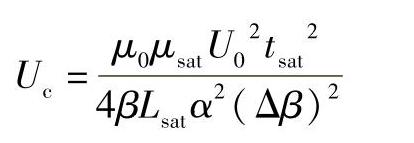
由于

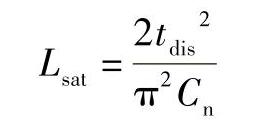
式中，t_dis是磁开关的放电时间。

故而

或有

由以上过程可知，除了分母中因子β和α²以外，式（5-7）与式（5-6）类似。既然定义式中有两个因子，那么磁开关设计所要求的体积就与β和α有很大的关系，因为叠层因子是由磁心结构决定的，设计者没有较大的α值变化余地。然而，可以通过调整磁心的高宽比值来实现包扎因子β的最大化，从而使得满足某种磁开关所需要的磁心体积最小。定义包扎因子为

令

此处m定义为磁心截面的宽高比，若m＝1，即Δr＝h，则磁心截面为正方形；若m＜1，则磁心截面的高度较其宽度大；若m＞1，其宽度较高度大。将式（5-9）代入式（5-8）中，有

定义

式中，γ为间隙与磁心宽之间的关联因子。式（5-10）可变为

式（5-11）可用图5-13所示来描绘，反映出对于几个不同的典型γ值，对应不同宽高比的包扎因子的变化情况。我们期望γ＝0，是绕线直接贴着磁心的情况，包扎因子是所有宽高比的集合。

(www.xing528.com)

图5-13 宽高比与磁开关包扎因子函数关系

然而，图5-13所示随着绕线与磁心的间隙增加，磁开关的包扎因子就急剧下降。另外，对于给定γ值时，磁开关的包扎因子是宽高比的函数，特别是对于给定γ值时，宽高比从1开始逐渐减小，磁开关的包扎因子急剧减小。对于γ不等于零时，包扎因子的最大值是在宽高比大于1的情况下得到的，此时包扎因子的减小速度相对于宽高比的增大速度慢一些。值得注意的是，随着γ值的增加，包扎因子的减小速度较宽高比的增加速度要快得多，这意味着随着绕线与磁心间间隙的增加，磁心体积对于磁心的宽高比的依赖性就会更大。

3.饱和时间的确定

磁开关饱和时间为

t_sat＝ΔBNA_c／U₀

即磁开关的饱和时间与选用磁心材料、N、A_c和磁开关输入端电压等有着密切的关系。这里ΔB＝B_r＋B_s，B_r为剩余磁感应强度，B_s为饱和磁感应强度。以磁开关L₁为例，其饱和的时间应该与C₁电荷转移至C₂时，C₂的电压上升时间（C₂充电时间）相比拟。C₂的电压上升时间为

t_L1＝π（L_1satC）^1／2

式中，C＝C₁C₂／（C₁＋C₂）。

4.磁开关压缩比的确定

设I_m为流过RSD的最大电流，那么总压缩比为

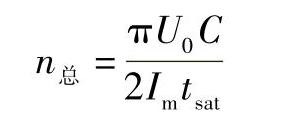
其中，t_sat既是磁开关的饱和时间，也是电容放电的电流上升时间。

磁开关电感值应满足下面条件

20L_ks≤L_（k-1）s≤L_k／20

又因为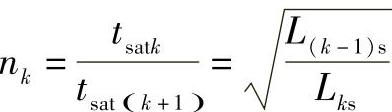，将其代入上式得到

设μ_k为初始磁导率；μ_ks为饱和磁导率；令μ_k＝μ_rμ₀，由于μ_ks＝μ₀，则上式即为

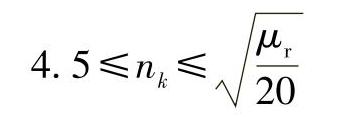
因为总压缩比n_总＝n₁n₂…n_k，故有

可以证明，若以最小磁心体积为目标函数，则每一级磁开关的压缩比为是最佳的。C₃的电压上升时间和下降时间为

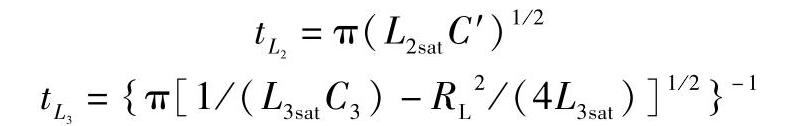
这里C′＝C₂C₃／（C₂＋C₃）。所以总脉冲压缩比为，第一级磁开关的脉冲压缩比为，为了提高R_L上的输出电压和电流上升率，可以考虑只用三级压缩后面以及R_L上并联一个电容C₄。因此第一级压缩的磁心体积可写为

5.磁开关截面积的确定

考虑包扎因子β和叠层因子α后磁开关截面积为

若使用环形磁心，设单个磁心的截面积为A_s时，则所需磁心个数即为

n＝A_c／A_s

这里，A_c与A_s的宽度相等。

6.磁心的工作损耗

仍以磁开关L₁为例，磁心损耗主要是磁开关未饱和阶段形成的，其铁耗功率为

式中，Δr为磁心宽度。

由于磁开关的匝数较少，所以重复频率不是很高，其铜耗比铁耗小得多，暂可忽略。

7.磁开关复位电路的设计

如图5-14所示，仍以三级磁压缩为例，当C₁向C₂充电时，脉冲电流流经磁开关时耦合至复位侧的电压与电流为

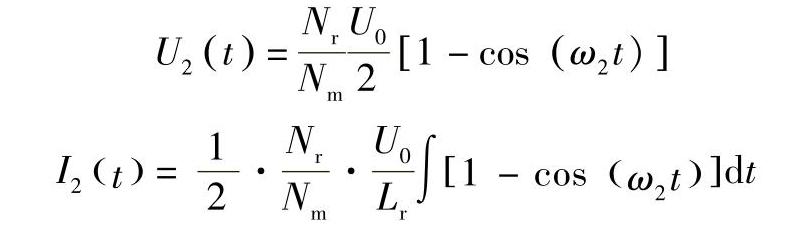
式中，U₀为磁开关两端的工作电压；N_m为主回路中磁开关线圈匝数；N_r为复位电路中磁开关线圈匝数；L_r为复位回路限流电感。

图5-14 用于磁开关复位的典型电路

如图5-15所示，磁开关饱和所形成的峰值电流为

式中，I₀为复位电源提供的复位电流。t＞t_sat时的复位电流为

i(t)＝I_pk[cosω(t-t_sat)]

式中，。磁开关复位所需要的时间为

式中，I_pk为复位线圈中的峰值电流，I_pk＝I₀＋ΔI＝I₀＋〈ut〉_rst／L_r；〈ut〉为通过磁开关复位线圈的复位电压时间积，〈ut〉_rst＝L_rI_pk[cos(ωt_sat)-1]。现以I_D＝0时的复位时间为标准，对复位时间进行标幺化，得到标幺复位时间为

图5-15 磁开关工作时复位回路中流经L_r的复位电流