电子空穴动力学在SOS效应模式下的探讨

SOS是借助于可控等离子层换流的思想来进行工作的。为说明SOS效应并研究SOS中的关断过程，S.A.Darznek等人建立了可分析大注入条件下电子—空穴动力学的模型。模型考虑了P^＋PNN＋结构的掺杂剖面及以下电子—空穴基本过程：强场中载流子的扩散和漂移、深能级杂质的复合、俄歇复合、密集等离子体的碰撞离子化。

在如图4-72所示电路中，描述电流的基尔霍夫方程为

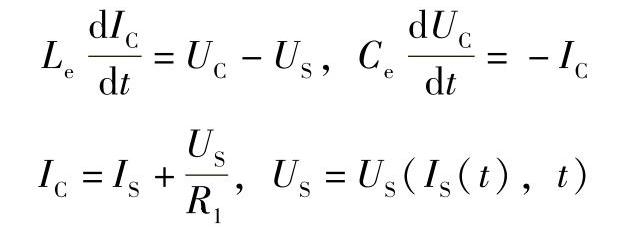
式中，U_C和I_C为等效电容上的电压和流过电容的电流；U_S和I_S为SOS上的电压和电流；C_e和L_e为电路的等效电容和电感，正向泵浦过程中分别为C^＋和L^＋，反向泵浦过程中分别为C^-和L^-。

变量U_C，I_C和U_S的初始条件为

U_C（0）＝U₀，I_C（0）＝0，U_S（0）＝0

图4-77为典型的SOS掺杂剖面结构，包括4个特征区域：通过扩硼获得的高掺杂P^＋区Ⅰ；通过扩铝获得的中等水平掺杂的P区Ⅱ；磷轻掺杂的N区Ⅲ；扩磷的N^＋区Ⅳ。二极管P^＋PNN＋结构在SOS效应机制下运行时，采用准中性等离子体近似，对非均匀掺杂半导体剩余等离子体浓度p有如下表达式

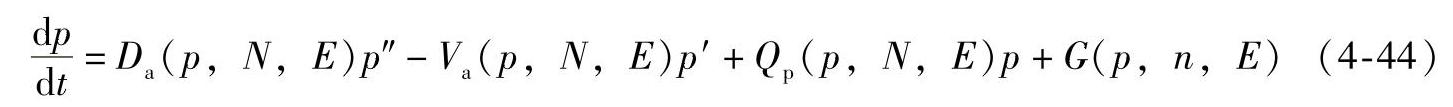
式中，D_a为双极扩散系数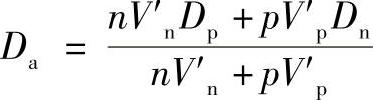，；V_a为双极漂移速率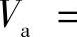，；Q_p为频率参数，；G为电子-空穴对的体产生率；电子和空穴的扩散系数分别为：D_n＝40cm²／s，D_p＝12cm²／s；符号“′”表示对其求导。

图4-77 SOS掺杂剖面图

在SOS的典型泵浦条件下，P^＋PNN^＋结构中会出现很高的电场，所以必须考虑函数V_n（E）和V_p（E）中漂移速率饱和的情况。采用插值公式：

式中，V_ns和V_ps分别为电子和空穴的饱和速率，V_ns＝107μm／ns，V_ps＝83μm／ns，在迁移率近似恒定情况下，V_n＝μ_nE和V_p＝μ_pE仍然有效；E_ns和E_ps为特征电场，E_ns＝7kV／cm，E_ps＝18kV／cm；β_n和β_p为调节系数，β_n＝1.11，β_p＝1.21。

式（4-44）适用于二极管结构的N区，位于PN结边界X_p的右边，这个边界相应于P型和N型杂质发生完全补偿的地方：N（x_p-n）＝0，空穴是少数载流子。在PN结左边的P区，电子是少数载流子，可得到类似的公式

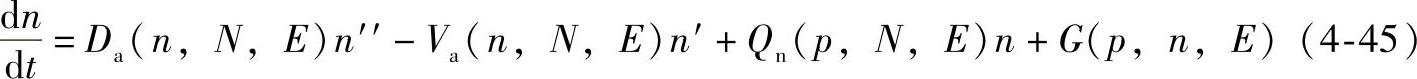
其中D_a，V_a为与式（4-44）中相同的双极系数。

为与Q_p有相似含义的频率参数。

以电子和空穴密度的平衡值作为函数n（x，t）、p（x，t）的初始条件，方程式（4-44）和式（4-45）的边界条件由二极管结构x＝0和x＝L处的金半接触特性决定，L为P^＋ PNN^＋结构的总长度。假设所有接触均为理想欧姆接触，载流子在二极管边界的密度相应于平衡密度：

n（0，t）＝n²_i／N_A（0）

p（L，t）＝n²_i／N_D（L）

其中n_i＝1.45×10¹⁰cm^-3为硅中本征载流子密度。(www.xing528.com)

电子—空穴对的体产生率是离子化率I和载流子复合率R的差值：

G（n，p，E）＝I（n，p，E）-R（n，p）

离子化率可表示为

I（n，p，E）＝α_n（n，p，E）n｜V_n（E）｜＋α_p（n，p，E）p｜V_p（E）｜式中，α_n0（E）和α_p0（E）为半导体中无移动载流子时的标准离子化系数，α_n（n，p，E）＝α_n0（E）β（n，p，E），α_p（n，p，E）＝α_p0（E）β（n，p，E）；β（n，p，E）为考虑载流子的影响。

α_n0（E）和α_p0（E）的插值公式为

α_n0（E）＝A_nexp（-B_n／｜E｜）

α_p0（E）＝A_pexp（-B_p／｜E｜）

式中，A_n，B_n，A_p，B_p均为调整系数，A_n＝7.4×10⁵cm^-1，B_n＝1.16×10⁶V／cm，A_p＝7.25×10⁵cm^-1，B_p＝2.2×10⁶V／cm。

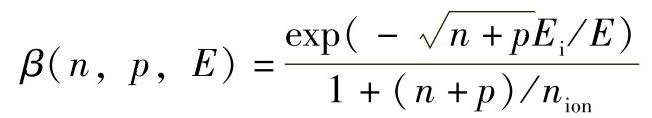
式中，E_i为硅离子化势能，E_i＝1.5V；n_ion为具有密度量纲的参数，n_ion＝2.4×10¹⁷cm^-3。

在高密度电子-空穴等离子体中，主要的复合过程为深能级杂质复合R_imp和俄歇复合R_Aug：

R_Aug＝（np-n²_i）（C_nn＋C_pp）

式中，τ_imp为粒子寿命；C_n，C_p为复合常数，C_n＝6×10^-31cm⁶／s，C_p＝3×10^-31cm⁶／s。

为了计算准中性等离子体模型的电场，引入总电流方程

j_d（t）＋j_c（t）＝j（t）

式中，j_d（t）为位移电流密度，j_d（t）＝ε·E；ε为硅电介质常数，ε＝11.7；j_c（t）为传导电流；j_c（t）＝q（D_nn′＋nV_n（E）-D_pp′＋pV_p（E））；电场的平衡剖面认为是初始分布E（x，0）。

通过二极管结构的电压计算公式为

U_L＝U_cont＋∫₀^LE（x）dx

式中，U_cont为接触电动势差，U_cont＝U_Tln（n（L）／n（0））；U_T为热电动势，U_T＝26mV。

U_S＝N_stU_L为SOS堆上的电压，N_st为串联二极管芯片数目。