非对称晶闸管最小长基区宽度WN（min）

非对称晶闸管的长基区宽度是协调通态电压与断态电压的重要参数，它还直接影响到器件的开通、关断时间和反向恢复特性，是设计晶闸管的基础。这里我们分两种情况对W_N（min）进行大致的定量讨论。

1）当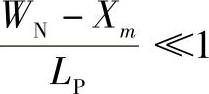，采用如普通晶闸管的近似设计方法。根据晶体管原理有

令γ＝1，将上式代入U_BR＝U_B（1-α₁）^1／n式得

又P^＋N单边突变结的空间电荷区宽度式可简化为

对Si而言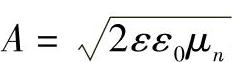，，当ε₀＝8.854×10^-14F／cm，ε＝11.7，A＝0.53，单位为μm。将人们常用的GE经验公式U_B＝Cρ^a与式（2-8）一起代入联解得

函数存在极小值，令dW_n／dρ＝0有

称ρ^∗为最佳电阻率。

以ρ^∗值代入式（2-9）可确定最小长基区宽度为

取常数α＝3／4、n＝6，上式可简化为

W_N（min）＝BL^2P／11·U_BO^21／22

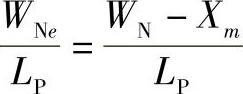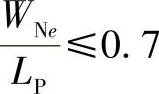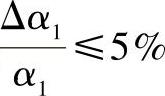代入各常数得到B＝0.0798。上式表明，最小长基区宽度决定于L_P与转折电压。当L_P较大，即越小时，由这种传统设计方法可以得到较为精确的W_N（min），通过计算分析认为，当，误差，当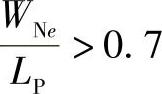甚至大于1的时候，传统的近似方法不再适用。

2）当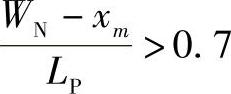，采用优化设计方法。与传统的近似设计相比，所不同的是引入优化比值K，

以U_B＝Cρ^a代入式（2-8）并表示为K值的形式，则

式中Q为常数，当U_BO给定，有

当W_Ne也表示K的形式，由晶闸管中的U_BR＝U_B（1-α₁）^1／n式得

α₁＝1-Kⁿ （2-10）(www.xing528.com)

假定γ＝1，由晶体管原理中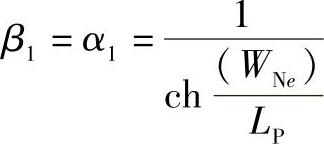，则有

由W_Ne和X_m可得到晶闸管长基区宽度W_N的表达式

分析计算表明，W_N（K）存在极值，且有

W″_N（K）＞0

有极小值存在。令W_N′（K）＝0，并代入各常数得

上式决定的极值点就是使W_N取得极小值的位置。以式（2-10）代入上式得

式（2-11）与式（2-12）即为用K表征和用α₁表征的晶闸管长基区优化设计公式。

可以代入各常数得到：

（1-α₁）^2／3＝4.1×10^-3（1／L_P）U_B0^7／6α₁（1＋α₁）^1／2

解上述超越方程可得到α₁，依次可求出K、U_B、ρ、X_m及W_eN。

所以长基区宽度为：

W_N＝X_m＋W_eN

假定一次扩散结深为X_jp，则硅片厚为

δ＝W_N＋X_jP

对于给定的U_BO和基区少子寿命，可以由求解上述两个超越方程，得到优化的K值或者α₁值，从而得到W_N（min）。理论和实践的结果表明，当τ_P较长或W_eN／L_P≪1时，传统的近似公式与实际有较好地吻合。在快速器件中，当W_eN／L_P＞1或在1附近的情况下，优化公式是很适用的。