GTO工作原理解析

图2-3所示为GTO的双晶体管模型，与普通的晶闸管的等效模型基本一样。

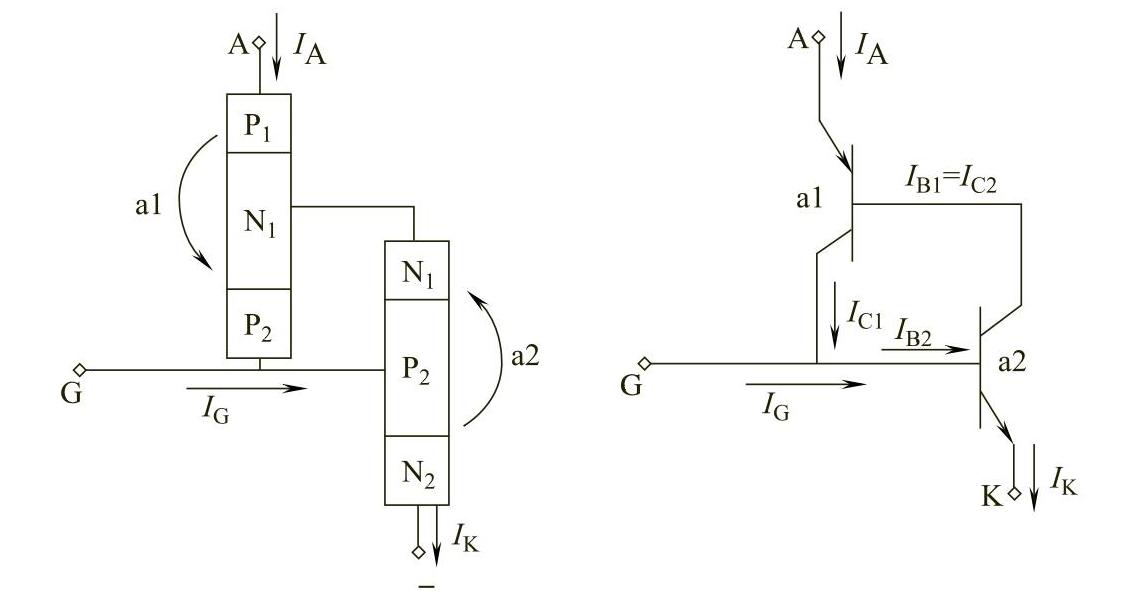
图2-3 GTO的等效模型

1.GTO的开通特性

GTO的开通特性与普通晶闸管相同，给门极加上一个正向电压，就可以使其进入开通状态，如图2-4所示，加上门极电流后，产生一系列的正反馈，使得GTO上的电流达到其维持电流，GTO开通。此外，GTO也可能因为其他的原因而开通，而其关断特性则和晶闸管有很大的不同。下面将重点介绍其关断特性。

图2-4 开通正反馈过程

2.GTO的关断原理

我们知道，对于PNPN结构的晶闸管，其维持导通的条件是电流放大系数α₁＋α₂＞1，这样才能使器件处于正反馈状态。当α₁＋α₂＜1，则晶闸管将会处于一个负反馈状态，流过器件的电流将会逐渐变小，最后关断。而对于GTO，其关断相比较于晶闸管要简单得多，可以方便地从门极加上一个负电压来使阴极电流减小，进一步导致阳极电流变小，使得α₁＋α₂＜1，引起关断负反馈，最后阳极电流减小为0，GTO关断。

在其双晶体管模型中，阳极电流可以表示为

I_A＝α₁I_A＋α₂I_K＝α₁I_A＋α₂（I_A-I_G）

则

由此，定义关断增益G_off为阳极电流和门极电流的比值，有

G_off表征GTO的关断能力的强弱。为了增强GTO的控制性，能够有效关断，希望G_off大一些，则α₁＋α₂必须尽可能接近1，而且α₂要大一些。对于同样的G_off，门极电流越大，其关断越有效。通常大功率的G_off做到5左右比较合适。

如图2-5所示，在GTO稳定开通后，在门极加上负的电压后，开始了抽取P基区过剩载流子，此阶段即为存储阶段t_s，GTO的所有等效晶体管均未退出饱和状态，J₁，J₂，J₃3个PN结都处于正向偏置状态，阳极电流仍然保持原先的稳定电流，管压降也基本保持开通时的水平。

当阳极电流下降到其开态电流的0.9倍时，存储时间结束，开始了下降时间阶段，此时，其两个等效的晶体管将退出饱和状态而进入放大状态，GTO的管压降从通态压降逐渐上升。由于阳极电流下降迅速，其di／dt太大，通过回路电感在GTO上产生一个电压突升的现象，此时，GTO上高电压可能使其恢复导通而引起关断失败，同时也会造成GTO的关断损耗增大。而实际上，通常在电路中会添加一个吸收电路（也称为缓冲电路）来限制器件上的电压变化率。当阳极电流下降为零时，器件关断。变为其通态电流的0.1倍时，下降时间结束。剩下的即为尾部时间，在此阶段，如上所述，GTO的关断首先是要从P基区抽取空穴，降低P基区的电位，使得J₃结开始反偏，关断区从近门极区域向远门极区域扩展，直到面积可以用载流子的扩散长度L_n的数量级来表示，这就是GTO关断的第一阶段，即存储阶段，也被称为二维关断阶段。

图2-5 关断时的波形图

对于PNPN型器件的关断，Wolley早期提出的一个理论描述了当横向电流主要由扩散电流构成时的关断模型。

如图2-6所示，GTO在关断的过程中，沿X轴方向被分为3个区域：通流区、关断区和通态区与关断区域之间的载流子扩散区。

对于P区域的过剩载流子浓度分布为二维分布，沿x-z平面过剩载流子浓度可以写为

n（x，z）＝n（z）f（x）

由于z方向电流主要为扩散电流，可以写为

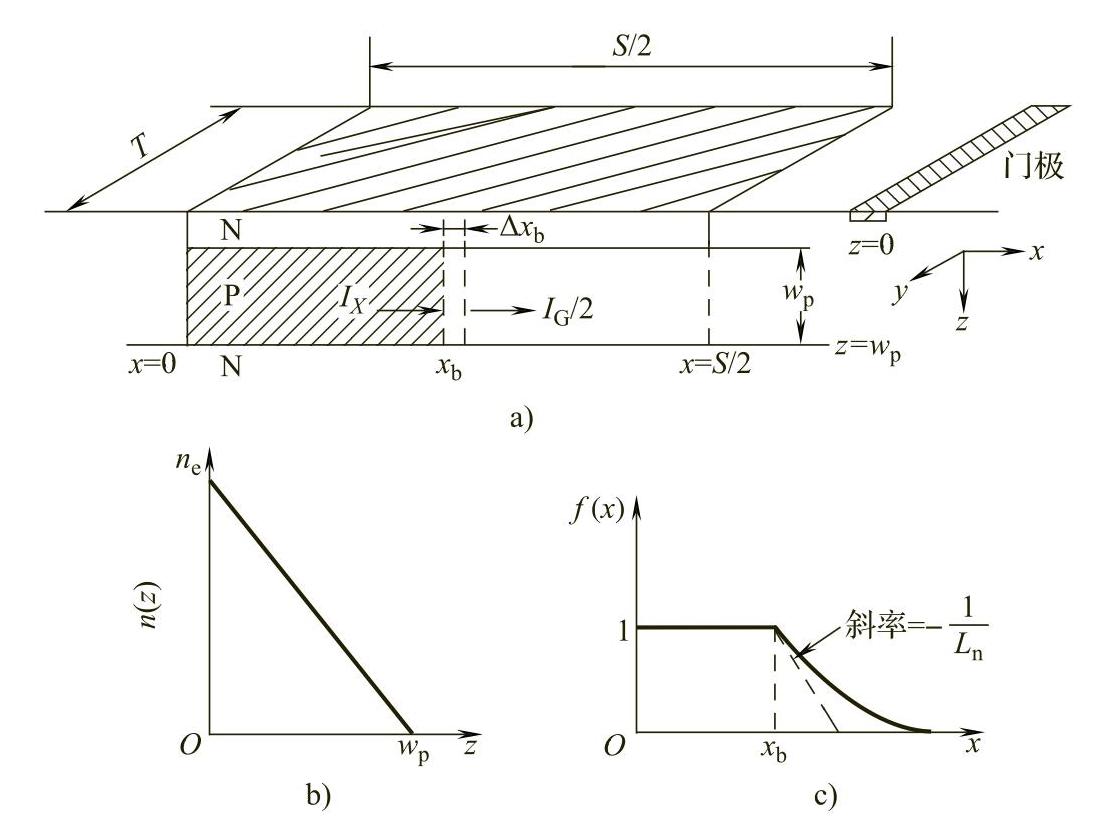
图2-6 Wolley模型简图

开通区域z方向电流恒定，其浓度梯度恒定，可写为

式中，n_e为J₁结面处的电子浓度。

解该方程可以得到

在x方向

这样，阴极电流可以写为

对（2-1）式进行移项变换可以得到

在x_b处沿X轴方向的扩散电流为

(www.xing528.com)

又在x_b处，横向电流和位置的关系可以表示为

将式（2-4）代入式（2-3）可以得到

在x_b处Δx_b宽度内少数载流子数目可以表示为

在x_b处，可近似取f（x_b）＝1，可得

而单位时间内过剩载流子的电荷的变化可以写为

将式（2-5）和式（2-6）的表达式代入式（2-7）可以得到

可以整理后得到

将其代入式（2-2），对Δx_b取极限可以得到

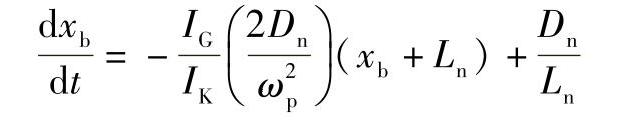
定义

得

定义存储时间为阴极区域被压缩到小于其扩散长度范围的时间，则

即为

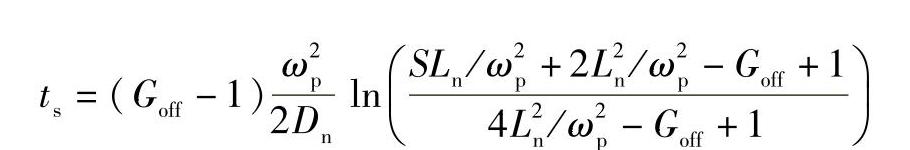
式中，S为阴极条宽；ω_p为P基区的厚度。

由上可以知道，当对数函数的分母接近于0时，存储时间会趋向于无穷大，限制了关断增益的值，由此可得

G_off（max）＝4L²_n／ω²_p＋1

式中，L_n为P₂区的少子寿命。对于大容量GTO，设计时一般取ω_p＝L_n。

当导通区域被压缩到很小时，此时的关断仅与阳极电流、门极电流和α₁＋α₂有关，称这一阶段为一维关断模型。一维关断原理和普通晶闸管的关断原理基本相似，可以根据双晶体管模型中的电流和α₁＋α₂的变化进行分析。此过程中，α₁＋α₂由大变小，当小于1后，回路由正反馈状态进入负反馈状态，最后GTO关断。

由于P₂区域的横向电流的作用，GTO的最大可关断阳极电流受到限制。如图2-2所示，I_G／2的电流流过P₂区域时，将会产生一个横向压降为

在关断中可以看到，外加的反向电压越高越有利于关断，但是由于J₃结两边的掺杂浓度比较高，这样J₃结的雪崩击穿电压就比较低，在正常的掺杂水平下，一般在20V左右。在J₃结的关断中，必须保证结面两边的电压低于J₃结的雪崩电压。这样，就限制了门极和阴极上所加的反向电压，一般为十几伏左右。

ΔU＜U_GR

这样可以得到门极的最大抽取电流为

I_G（max）＜4U_GR／R_b

由G_off＝I_A／I_G，可以得到

I_A（max）＜4U_GRG_off／R_b

上式表明，为了获得高的阳极可关断电流，基区横向电阻R_b要小，因此P₂区的掺杂浓度比普通晶闸管中的要高。但过高的掺杂浓度也会导致发射结击穿电压降低；通态电压增大，门极触发电流增大。所以必须选取最佳的P₂区掺杂浓度，据资料，P₂区的掺杂在0.5×10¹⁸～1.5×10¹⁸cm^-3值可以获得令人满意的折中。为了提高该最大电流，还可以在一定范围内减小阴极条的条宽，这样就缩短了横向距离，也达到减小横向电阻的目的。

为了减小R_b，GTO一般采用多阴极结构，实际的GTO中多采用多叉指结构。研究表明，最大的门极关断电流与GTO的单元数的平方根成正比。同时，最大的门极关断电流随阴极指宽的减小而增加，现今GTO的指宽通常在250～300μm。双叉指层图形由浅和深的扩散N±阴极层交错形成，以使关断期间阴极指中心电流分布最佳。利用该图形，其最大阳极电流可以提高20％，且有很高的du／dt耐量。