二阶系统频率响应优化指南

将传感器看作二阶系统，其微分方程的拉普拉斯变换表达式：

传递函数表达式：

频响函数表达式：

其幅频特性表达式：

取对数后表达式为

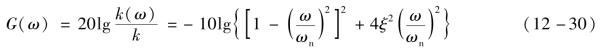
相频特性表达式：(www.xing528.com)

二阶系统的频响伯德图如图12-12 所示。

(1)当ω/ωn ≤1(即ω ≪ωn )时，k(ω)= k，φ(ω)= 0 ，即近似于理想的系统(零阶系统)。要想使工作频带加宽，最关键的是提高无阻尼固有频率ωn。

(2)当ω/ωn →1(即ω →ωn )时，幅频特性、相频特性都与阻尼比ξ 有着明显的关系。可以分为三种情况：

①当ξ ＜1(欠阻尼)时，K(ω)在ω/ωn ≈1(即ω →ωn )时出现极大值，即出现共振现象。当ξ =0 时，共振频率就等于无阻尼固有频率ωn ；当ξ ＞0 时，有阻尼的共振频率为 ，值得注意的是，这与有阻尼的固有频率是稍有不同的，不能混为一谈。另外，φ(ω)在ω →ωn 时趋近于-90°。一般在ξ 很小时，取ω ≪ωn/10 的区域作为传感器的通频带。

②当ξ ≈0.7(最佳阻尼)时，幅频特性K(ω)的曲线平坦段最宽，而且相频特性φ(ω)接近于一条斜直线。这种条件下若取ω = ωn/2 为通频带，其幅度失真不超过2.5%，但输出曲线要比输入曲线延迟Δt = π/2ωn。

③当ξ =1(临界阻尼)时，幅频特性曲线永远小于1。相应地，其共振频率ωd = 0 ，不会出现共振现象。但因为幅频特性曲线下降太快，平坦段反而变得小了。值得注意的是，临界阻尼并非最佳阻尼，不应混为一谈。

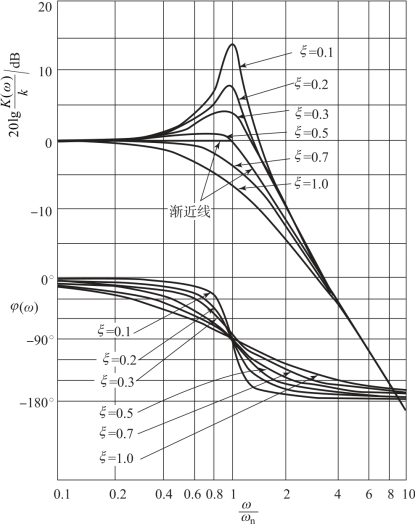
图12-12 二阶系统的频响伯德图

(3)ω/ωn ≫1(即ω ＞ωn )时，幅频特性曲线趋于零，几乎没有响应。

综上所述，用二阶系统描述的传感器动态特性的优劣主要取决于固有频率ωn 或共振频率ωd =。对于大部分传感器因为ω ≪1 ，故ωn 与ωd 相差无几就不再详细区分。另外，适当地选取ξ 值也能改善动态响应特性，它可以减少过冲、加宽幅频特性的平直段，但相比之下不如增加固有频率的效果更直接更明显。