【摘要】：给传感器输入阶跃信号并记录其响应曲线，确定其时间常数，多种确定方法如下。图12-10 一阶系统阶跃响应图12-11 一阶系统冲击响应作图法：根据一阶系统阶跃响应曲线，在输出yn= 0.632k 时，其对应的时间t =τ。只要记录足够长的阶跃响应曲线，可以得到稳态响应值的幅值，取该幅值的63.2%作一水平线与曲线相交，相交点对应的时间即为时间常数。
一阶系统只要确定其时间常数τ，其传递函数就可以确定。给传感器输入阶跃信号并记录其响应曲线，确定其时间常数，多种确定方法如下。一阶系统的阶跃响应和冲击响应曲线如图12-10 和图12-11 所示。
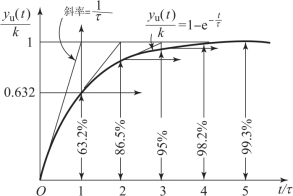
图12-10 一阶系统阶跃响应
图12-11 一阶系统冲击响应
(1)作图法：根据一阶系统阶跃响应曲线，在输出yn(t)= 0.632k 时，其对应的时间t =τ。只要记录足够长的阶跃响应曲线，可以得到稳态响应值的幅值，取该幅值的63.2%作一水平线与曲线相交，相交点对应的时间即为时间常数。
(2)计算法：一阶系统阶跃响应函数为yu(t)= k(1- e-t/τ)，化简为(www.xing528.com)
当
时yu/k →1 ，取响应曲线的稳态值为1，就相当于得到了(yu/k)作为t 的函数曲线。取新变量z：z = 
实验得到阶跃响应曲线上取若干个点，测量每个点相应的t 和(yu/k)值并计算z 值，得到n 组数据，就可在t 和z 组成直角坐标图上标出n 个点，对n 个点拟合一条直线，该直线的斜率就是时间常数τ：
该方法利用了响应曲线上多个点，通过直线拟合有效地消除了随机干扰的影响和零点难以准确判断等困难，其结果较可靠。同时，通过z-t 图上数据点与直线靠近的程度，判断该传感器响应特性是否适宜用一阶系统可靠描述。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
