热电偶的物理原理及应用

1.热电效应

两种不同导体A 与B 串接成闭合回路，如果两结合点1 和2 存在温差，在回路中就有电流产生，这种由于温度不同而产生电动势的现象称为热电效应或塞贝克效应，这两种不同导体的组合称为热电偶，如图7-1 所示。

接点1 通常用焊接的方法连接在一起，测温时置于被测温场中，称为测温端、热端或工作端。接点2 处于恒定不变的温度场，称为参考端、冷端或自由端。热电偶产生的热电势EAB(T，T0)是由两种导体的接触电势(珀尔帖电势)和单一导体的温差电势(汤姆逊电势)所组成。

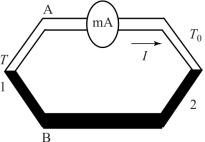
图7-1 热电效应示意图

1)两种导体的接触电势(珀尔帖电势)

导体中含有大量的自由电子，不同金属自由电子密度不同。假设金属A、B 的自由电子密度分别为nA、nB，并且nA ＞nB ，A、B 金属接触在一起时，A 中自由电子向B 扩散，这时A 失去电子而具有正电，B 得到电子而带负电，扩散达到动态平衡，达到稳定的接触电势，如图7-2 所示。

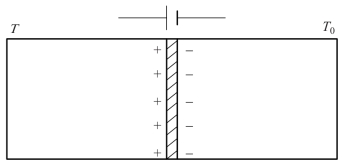
图7-2 两种导体接触电势

珀尔帖电势数学表达式为

式中，k 为玻耳兹曼常数(1.38 ×10 -23 J·K)；e 为电子电荷量( 4.803 ×10-10 静电单位)；T 为接触点绝对温度；nA、nB 为金属A、B 中的自由电子密度。

热电偶回路总的接触电势：

T = T0 时，总的接触电势为零。

2)单一导体的温差电势(汤姆逊电势)

对单一均质导体来说，两端温度不同(如T ＞T0 )，则在两端也会产生电动势EA(T，T0)，这个电势叫作单一导体的温差电势，也称汤姆逊电势，如图7-3 所示。

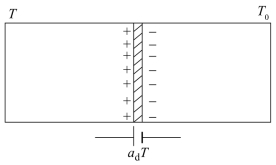
图7-3 汤姆逊电势

汤姆逊电势的形成是由于高温端导体内自由电子有较大的动能，因而向低温端扩散，由于高温端失去电子而带正电，低温端得到电子而带负电，从而形成汤姆逊电势，数学表达式为

式中，σA 为汤姆逊系数，与金属材料有关。

A、B 导体构成的热电偶回路，总汤姆逊电势数学表达式为

这个电势与热电材料A、B 和温度T、T0 有关。若T = T0 ，积分为零，即汤姆逊电势为零。若A、B 相同，则σA = σB ，汤姆逊电势也为零。

3)总热电势

总热电势由珀尔帖电势和汤姆逊电势构成，数学表达式为

式(7-5)表明：

(1)如果热电偶两电极材料相同，虽两端温度不同，热电偶总输出热电势仍为零，因此热电偶必须由两种不同材料构成。

(2)如果热电偶两端点温度相同，则总热电势为零。

(3)热电势的大小与热电偶尺寸、形状及沿热电极温度分布无关，只与材料和端点温度有关。若热电极本身材质不均匀，由于温度梯度存在将会有附加电势产生。

2.热电偶基本定律

1)均质导体定律根据总热电势数学表达式，由一种均质导体组成闭合回路，尽管两端有温差存在，但由于nA =nB，σA =σB，所以：

(www.xing528.com)

上式表明：均质导体构成回路总热电势为零，不能用于测温。

2)中间导体定律

热电偶实际测温过程必须在回路引入测量导线和仪器仪表，能否影响热电势测量?

中间导体定律表明：热电偶测温回路，只要中间导体两端点温度相同，接入中间导体后对热电偶回路的总热电势没有影响。

图7-4 所示为热电偶回路中接入中间导体C 的情况。图7-4(a)表明，中间导体C与导体A、B 两个接点处保持相同温度T0。

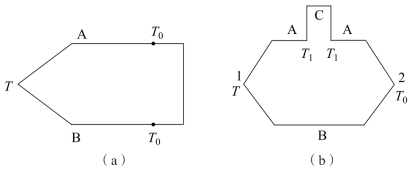
图7-4 热电偶接入中间导体的回路

未接入中间导体C 之前，冷端(参考端)T0 的热电势为

接入C 后热电势为

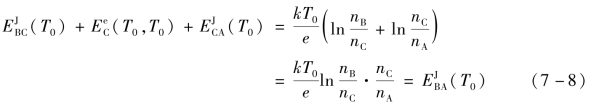
图7-4(b)表明：A 断开处和C 两端点温度均为T1 ，引入后无影响。

3)连接导体定律

如图7-5 所示，连接导体定律指出：在热电偶回路中，如果热电极A、B 分别与连接导线An、Bn 相连接，端点和接点温度为T、Tn、T0，回路热电势EAB(T，Tn)为连接导线An、Bn 在温度Tn、T0 时的热电势EAnBn(Tn，T0)的代数和，数学表达式为

4)中间温度定律

根据式(7-9)，当A 与An，B 与Bn 材料分别相同，且接点温度为T、Tn、T0 时，该回路的热电势为

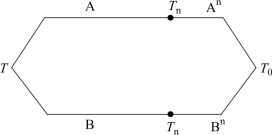
图7-5 用连接导线的热电偶回路

上式表明：热电偶在接点温度为T、T0 时热电势EAB(T，T0)，等于热电偶在(T，Tn)、(Tn，T0)时，相应热电势EAB(T，Tn)与EAB(Tn，T0)的代数和，这就是中间温度定律，Tn 称为中间温度。

同一种热电偶参考端温度不同，其产生的热电势也不同，要将对应各种(T，Tn)温度的热电势-温度关系都列成图表烦琐，中间温度定律为简化热电偶分度表的制定奠定了理论基础。根据中间温度定律，只要列出参考端温度为0℃时的热电势-温度关系，那么参考端温度不为零度时的热电势测出后，可按上式查分度表确定测端温度T。

假设用镍铬-镍硅热电偶测量某温度，参考端温度Tn =25℃，仪表测得热电势E(T，Tn)为28.55 mV，试求实际被测温度T 值。

解答：先查镍铬-镍硅热电偶分度表，得到下式：

依据中间温度定律：

E(T，T0)= E(T，Tn)+(Tn，T0)= 28.55 +1.00 =29.55(mV)

所得29.55 mV 才是热电偶工作端温度为T，参考端温度为0℃时产生的热电势，以此热电势再查上述分度表，就可得工作端温度，即被测温度T=710℃。

在用热电偶实际测温时，往往参考端不是0℃，此时不能由仪表所测得的热电势直接去查分度表，应该修正后再查表得工作端温度。

5)参考电极定律

如图7-6 所示，已知热电极A、B 分别与参考电极C 组成的热电偶在接点温度为T、T0时的热电势，在相同接点温度( T，T0 )，由A、B 两种热电极配对后的热电势数学表达式为

图7-6 参考电极回路

参考电极定律简化了热电偶选配工作，只要我们获得有关热电极与标准铂电极配对的热电势，任何两种热电极配对时的热电势便可按式(7-12)求得，而不须逐个测定。