1.理想液体和稳定流动
研究液体流动必须考虑黏性和压缩性的影响,但由于问题复杂,可以假设液体是没有黏性和不可压缩的,然后通过实验验证的方法在理想结论的基础上进行修正。这种假设液体称为理想液体。
液体流动时,若液体中任一点处压力、速度、密度都不随时间而变化,这种流动称为稳定流动。反之,只要压力、速度、密度有一个随时间变化,就称为非稳定流动。
2.过流断面、流量和平均流速
过流断面:液体在管道内流动,垂直于液流方向的截面。其面积常用A 表示,单位为m2。
流量:单位时间内流过某一过流断面的液体体积。用qv表示,单位为m3/s 或L/min。
假设理想液体在一直管内做稳定流动,管道截面积为A,过流断面上各质点的流速u 相等,则时间t 内流过某一过流断面的液体体积V=Aut,所以流量为
![]()
由于液体的黏性,过流断面上各点的速度并不相等,也难以确定,如图1-4-1 所示。为此,科学家提出了平均流速的概念,用υ 表示,即假设过流断面上各点流速均匀分布,且有如下流量关系式:
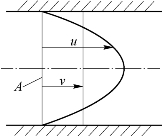
图1-4-1 平均流速
![]()
从而得出过流断面上的平均流速为
![]()
在液压缸工作时,活塞的运动速度等于缸内液体的平均流速。因此,活塞运动速度υ活与液压缸有效面积A、qv 之间的关系为

当液压缸有效面积一定时,活塞运动速度取决于进入液压缸的流量。
3.层流、紊流、雷诺数(https://www.xing528.com)
实际液体流动时具有两种状态,即层流和紊流。可以通过雷诺实验观察这两种现象。
实验装置如图1-4-2 所示,实验时保持水箱中水位恒定,然后将阀门8 微微开启,使少量水流流经玻璃管,玻璃管内平均流速υ 很小。这时,如将容器的阀门4 (实验中使用红色水)开启,使水流入玻璃管内,在玻璃管内看到一条明显的直线流,不论红色水放在玻璃管内的什么位置,它都呈直线状,这说明管中红色水和周围的液体没有混杂,管中水流是分层的,层与层间互不干扰,这种流动状态就是层流。如果把阀门8 缓慢开大,管中液流平均流速υ 增加至某一数值,红色水流开始弯曲颤动,这说明玻璃管内液体层流被破坏,液流紊乱。如果阀门8 继续开大,平均流速υ 进一步加大,红色水流完全与周围液体混合,红色水流完全消失,这种流动状态称为紊流。
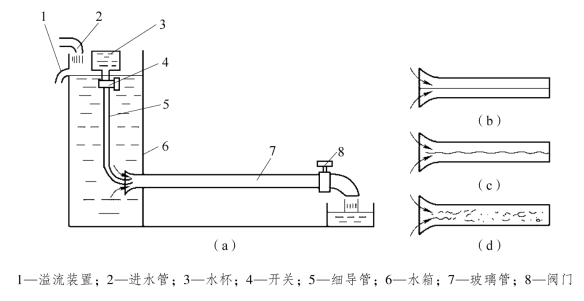
图1-4-2 雷诺实验装置
(a)实验装置;(b)层流;(c)过渡状态;(d)紊流
如果将阀门8 逐渐关小,则玻璃管中流动状态又从紊流向层流转变,但转变时阀口面积要比由层流向紊流转变时要小。
实验证明,液体在圆管中流动状态不仅与管内平均流速υ 有关,还与管径d 和液体的运动黏度ν 有关,3 个参数组成了一个判定液体流动状态的无量纲数,即雷诺数Re。
![]()
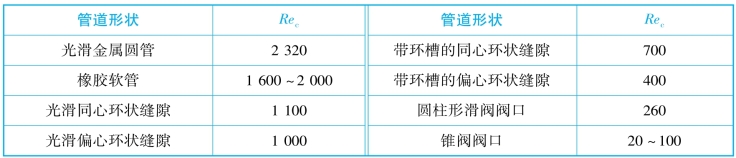
液流由层流向紊流转变时的雷诺数和由紊流向层流转变时的雷诺数是不同的,后者数值小,所以一般工程中用后者作为判断液流状态的依据,称为临界雷诺数,记为Rec,当实际雷诺数小于Rec 时为层流,反之为紊流。常见液流管道的临界雷诺数见表1-4-1。
表1-4-1 常见液流管道的临界雷诺数
雷诺数的物理意义:雷诺数是液流惯性力与黏性力的比值。当雷诺数较大时,惯性力起主导作用,为紊流;当雷诺数较小时,黏性力起主导作用,为层流。雷诺数相同,流动状态相同。
例1-2 液体在光滑钢管中的平均流速为υ=4 m/s,管道内径d=80 mm,油液的运动黏度ν=40 mm2/s,试判定液体的流动状态。若要保证为层流,其流速应为多少?取Rec=2 320。
解:由雷诺数公式
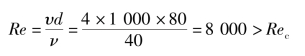
因此,液体流动状态为紊流。
若保证层流时,平均流速为
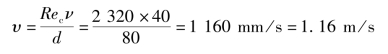
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




