热力除氧的理论基础及原理

热力除氧以亨利定律、道尔顿定律为理论基础，用加热给水的方法来除去水中溶解的气体。

1.亨利定律

亨利定律指出：在一定的温度下，当溶解于水中的气体与自水中离析的气体处于动平衡状态（气体溶解量与离析量相等）时，气体在水中的溶解度与水面上该气体的分压力成正比，即单位体积水中溶解的某气体量b与该气体在水面上的分压力pb成正比，其表达式为

式中　b——气体在水中的溶解量，mg/L；

pb——平衡状态下水面上气体的分压力，Pa；

p0——水面上气体混合物的全压力，Pa；

K——气体的质量溶解度系数，该系数随气体种类和温度而定，mg/L。

如图4-1所示，在一定压力下，氧气和二氧化碳气体在水中的溶解度随着温度的升高而降低。

图4-1　气体在水中的溶解量与水温的关系

（a）水中O2的溶解度；（b）水中CO2的溶解度

由亨利定律可知，如果水面上某气体的实际分压力p小于水中溶解的该气体所对应的平衡压力pb，那么该气体就会在不平衡压差Δp（Δp=pb-p）的作用下，从水中离析出来，于是水面上该气体的分压力p增大，直至达到新的平衡状态为止。如果把气体从水面上完全清除，使其实际分压力p为零，则在不平衡压差Δp的作用下，就可以将水中溶解的该气体完全除去。

2.道尔顿定律

道尔顿定律指出：混合气体的全压力等于其各组成气体的分压力之和。由此可知，在热力除氧器中，水面上混合气体的全压力p0应等于水中溶解的各种气体（O2、N2、CO2、水蒸气等）的分压力之和，即

(www.xing528.com)

由此可知，道尔顿定律提供了将水面上不凝结气体的分压力降为零的方法。在定压下将给水加热，随着水的不断蒸发，水面上蒸汽的分压力逐渐增大，同时其他气体的分压力逐渐降低。当将水加热到除氧器工作压力下的饱和温度时，水大量蒸发，水蒸气的分压力就会趋近于水面上的全压p0，于是水面上其他气体的分压力∑pj就会趋近于零，从而形成了水中溶解气体的不平衡压差，因此溶解于水中的气体就会从水中逸出而被除去。

3.传热方程与传质方程

在热力除氧中，既存在传热（加热给水）过程，又存在传质（气体自水中离析出来）过程，因此，要达到除氧目的，必须将给水迅速加热至除氧器工作压力下的饱和温度，使水蒸气的分压力趋近于水面上的全压，∑pj才会趋近于零，如果水面上氧气的分压力为零，水中溶解的氧量就会为零，否则，即使有少量的加热不足，水中溶氧量都会超过除氧指标要求。如图4-2所示，在大气压力下，水温加热不足为1℃时，水中含氧量就高达0.2mg/L，远远超过允许值。如果用Qd（kJ/h）表示除氧器传热量，Kh[kJ/（m2·℃·h）]表示传热系数，A（m2）表示汽水接触的传热面积，Δt（℃）表示传热温差，则传热方程为

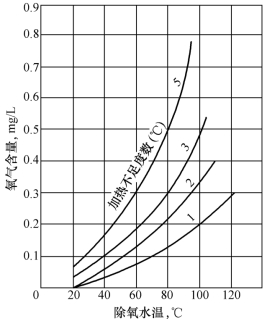
图4-2　水中溶氧与水温加热不足的关系

另外，气体自水中逸出时，要具有足够的动力，即不平衡压差Δp，所以必须将水中离析出来的气体及时排除，以使水面上氧气等气体的分压力趋近或等于零。气体自水中离析出来的量可由传质方程表示，即

式中　G——离析气体量，mg/h；

Km——传质系数，mg/（m2·Pa·h）；

A——传质面积，m2；

Δp——不平衡压差，Pa。

由式（4-4）可知，热力除氧还受到传质面积（加热蒸汽与被除氧水的接触面积）的影响，所以在除氧器设计和运行中，提供足够的汽水接触面积和充裕的传热传质时间，并保证尽可能大的不平衡压差，有利于促进水中气体的离析，提高除氧效果。

气体自水中离析出来的过程可分为初期除氧和深度除氧两个阶段。

初期除氧阶段，水中溶解的气体较多，不平衡压差较大，气体以小气泡形式克服水的表面张力而从水中离析出来的驱动力较大，因此能除去水中气体的80%～90%，水中含氧量可降低到0.05～0.1mg/L。

深度除氧阶段，水中仅残留少量气体，不平衡压差已很小，气体已难以克服水的表面张力离析，只能依靠单个分子的扩散作用慢慢逸出。此时，可以通过加大汽水接触面积，使水形成水膜，因水膜的表面张力小，所以气体易于扩散出来。另外，也可以通过蒸汽在水中的紊流来强化扩散作用，使气体附着在气泡上面从水中离析出来。