电厂能量质量利用研究：分析法详解

（一）的一般概念

热量法不能反映能量在质量上的差别，而状态参数可以满足这一要求。和能量的概念在本质上是有区别的。是一个特定的概念，它表示在给定的环境条件下，能量具有的最大做功能力。在某种程度上可以理解为能够被利用的能量，损可以理解为损失掉的可被利用的能量。分析法是利用效率（可用能利用率）和损（做功能力损失）来评价电厂能量的质量利用情况。

1.热量（热流）

热量是过程量，如图1-6所示，1kg工质在变温情况下沿1-2过程吸热，吸热量为q12。取一微元吸热过程的吸热量为dq，工质熵的变化为ds，则dq=Tds，根据热力学第二定律，热流dq所能完成的最大功，即热流dq的deq，其计算式为

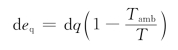
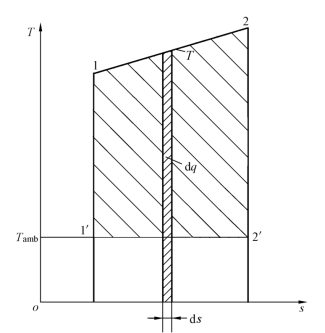
图1-6　变温传递热量的

热量q12的为面积122′1′1，其计算式为

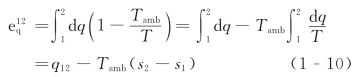
假定吸热过程的平均温度为，则

由式（1-11）可知，热流的大小不但与热量的数量有关，而且与过程的温度有关，过程平均温度越高，热量就越大，热量的品位也就越高。

2.工质

工质在稳定流动中由给定的状态可逆地变到与环境相平衡的状态所能完成的最大有用功称为工质。

如图1-7所示，1kg工质进入热力系统时的参数p1、t1可逆地变到与环境相同的参数pamb、tamb，在状态变化时，没有其他热源，只与环境交换热量，并对外做功。忽略工质动能和位能的变化，则由热力学第一定律可得

根据热力学第二定律

将式（1-12a）代入式（1-12）并整理，可得1kg工质在状态p1、t1下的为

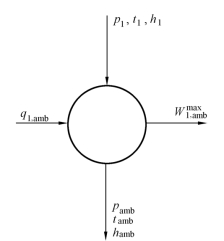
图1-7　能量平衡示意图

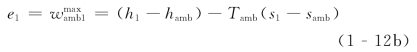
式中　h1——给定状态工质的焓，kJ/kg；

s1——给定状态工质的熵，kJ/（kg·K）；

hamb——环境状态工质的焓，kJ/kg；

samb——环境状态工质的熵，kJ/（kg·K）；

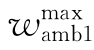——热力系统对外做的最大功，kJ/kg。

3.其他有关能量的

理论上，机械能和电能都可以全部转变为功，所以

机械能的=机械能的热当量

电能的=电能的热当量

固体燃料的化学=固体燃料的低位发热量

4.损失、平衡和效率

各种热力过程的不可逆因素都将会有熵增，熵增将带来做功能力的损失即损失，它使一部分可用能变成无用能，也就是说，不可逆过程是不守恒的。因此，对任何实际热力过程来说，热力系统输出各种的总和永远小于进入热力系统的总和，两者之差就是热力过程的损失ΔE1，即

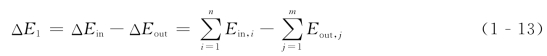
式中　ΔEin、ΔEout——进、出热力系统的任何形式的。

式（1-13）是开口热力系统平衡的通用方程。通过该方程可以求出某一热力设备或整个发电厂的损失。整个发电厂的损失ΔE1，cp等于能量转换过程中各有关热力设备损失总和，即

式中　ΔEl，i——某一热力设备或能量传递过程中的损失。

损失可以用作评价热力设备和发电厂热经济性的指标，但它是个绝对数值，不便于与其他热力设备进行相互比较，所以引入相对指标——效率。

常用的效率的定义是有效利用的与消耗的之比，有时也称其为第二定律效率。例如，燃煤凝汽式发电厂煤耗为B，总损失为ΔE1，cp，发电功率Pe，则其效率ηe，cp为

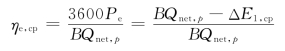
需要说明的是，这里把煤的化学能近似地等于其低位发热量。(https://www.xing528.com)

采用相似的方法可计算发电厂各热力设备的效率。

（二）发电厂的分析

以图1-1（a）所示简单凝汽式发电厂为例，按能量转换顺序，分析各设备中的损失及发电厂的效率。

分析按工质流量1kg为基准，并忽略水在给水泵中的焓升，即给水的焓等于主凝结水的焓。根据给定的有关汽水参数及各热力设备的效率，可求出需要燃料提供的热量及热力系统各有关的。

1.锅炉中的损失

锅炉的平衡式为

锅炉的损失Δel，b为

2.主蒸汽管道的损失

主蒸汽管道的平衡式为

eb=e0+Δel，p

蒸汽流经主蒸汽管道时的损失Δel，b为

Δel，p=eb-e0

3.汽轮机内部损失

汽轮机的平衡式为

e0=wi+ec+Δel，tu

汽轮机内部的损失为

Δel，tu=e0-wi-ec=e0-（h0-hc）-ec

式中　wi——蒸汽在汽轮机中所做的内功。

4.凝汽设备的损失

凝汽设备的平衡式为

凝汽设备中的损失为

在该系统及特定条件下，

5.汽轮机机械摩擦阻力引起的损失

汽轮机轴端输出的有效功为we=wiηm=（h0-hc）ηm，故汽轮机机械摩阻引起的损失Δel，m为

Δel，m=wi-we=（h0-hc）（1-ηm）

6.发电机的效率

发电机输出的电能为wel=weηg=（h0-hc）ηmηg，故发电机中的损失e1，g为

e1，g=we-wel=（h0-hc）ηm（1-ηg）

7.发电厂的效率

发电厂的总的损失Δe1，cp为各项损失的总和，即

Δe1，cp=Δe1，b+Δe1，p+Δe1，tu+Δe1，c+Δe1，m+Δe1，g

发电厂的效率为

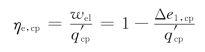
发电厂的平衡方程式为

以燃料eq为100%，算出电能及各项损失所占份额后，便可绘制发电厂的流图。图1-8为蒸汽初参数为13MPa、535℃，终参数为5kPa的简单凝汽式发电厂的流图。

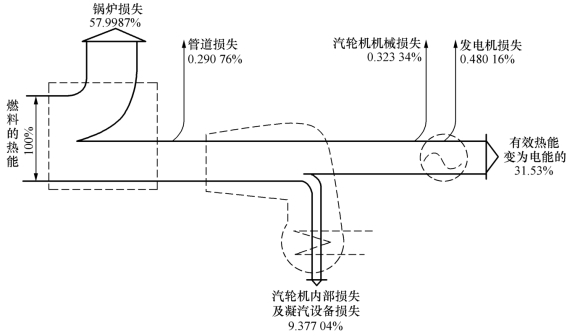
图1-8　超高压简单凝汽式发电厂的流图