数学处理方法：如何合理选择图形？

对零件图进行数学处理是编程前的主要准备工作之一，不但对手工编程来说是必不可少的工作步骤，而且即便采用计算机进行自动编程，也经常需要先对工件的轮廓图形进行数学预处理，才能对有关几何元素进行定义。

非圆曲线处理包括除圆以外的各种可以用方程描述的圆锥二次曲线（如抛物线、椭圆、双曲线）、阿基米德螺旋线、对数螺旋线及各种参数方程、极坐标方程所描述的平面曲线与列表曲线等。数控机床在加工上述各种曲线平面轮廓时，一般都不能直接进行编程，而必须经过数学处理以后，采用相互连接的直线逼近和圆弧逼近方法，才能通过设置宏变量（或参数）和演算式，并引入加工程序，同时在加工程序中使用逻辑判断语句进行编程。下面将分别介绍常用的直线逼近和圆弧逼近的数值计算方法。

1.直线逼近法

一般来说，由于直线逼近法的插补节点均在曲线轮廓上（图3-5），容易计算，程编也简便一些，所以常用直线逼近法来逼近非圆曲线。其缺点是插补误差较大，但只要处理得当还是可以满足加工需要的，关键在于插补长度及插补误差控制。

由于各种曲线上各点的曲率不同，如果要使各插补段长度均相等，则各段插补的误差大小不同。反之，如果要使各段插补误差相同，则各插补段长度不等。下面介绍常用的手工编程拟合计算方法。

（1）等间距直线逼近法 等间距直线逼近法是在一坐标轴方向，将拟合轮廓的总增量（如果在极坐标系中，则指转角或径向坐标的总增量）进行等分后，对其设定节点所进行的坐标值计算方法，如图3-6所示。

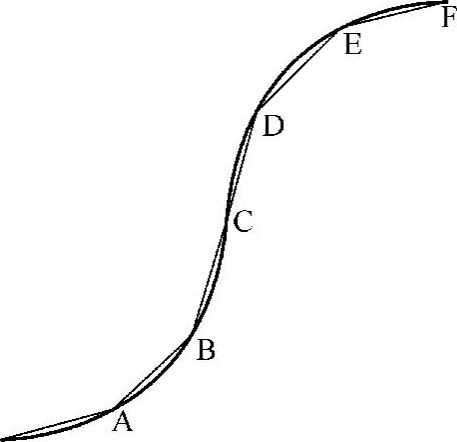
图3-5 零件轮廓的节点

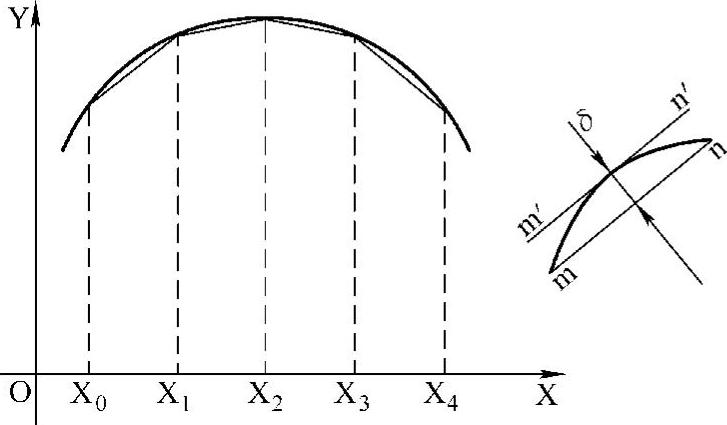
图3-6 等间距直线逼近法

已知方程Y=f（X），根据给定的ΔX求出X_i，将X_i代入Y=f（X）即可求得一系列的（X₀，Y₀），…，（X_i，Y_i），即每个线段的终点坐标，并以该坐标值编制直线程序段。

ΔX取决于曲线的曲率和允许误差δ，一般δ取零件的1/10～1/5，验算的方法如图3-6所示。mn为计算后某一逼近线段，作m′n′平行于mn并与曲线相切，切点至mn的距离为δ，若求得mn的方程为

AX+BY+C=0

则m′n′的方程为

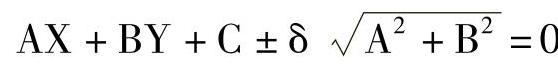
求解联立方程：

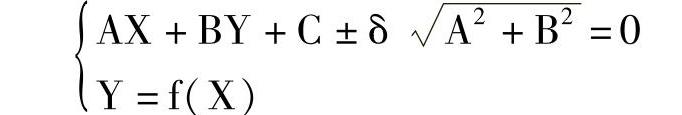
当该方程组有一解或无解时，即可满足精度要求。等间距直线逼近计算简单，但由于取定值ΔX，在曲率变化较大时，程序段数较多。

采用这种方法进行手工编程时，容易控制其非圆曲线或立体型面的节点，因此，宏（参数）程序编程普遍采用这种方法。但由于用直线逼近曲线时，工件轮廓是由许多折线构成的近似线段，连接点处不光滑，而且直线的曲率半径无穷大，与原有曲线的曲率半径相差很大。使用圆弧逼近可以避免这些缺点。

（2）等插补段直线逼近法 等插补段直线逼近法即是所有逼近线段的长度都相等，如图3-7所示。

例：为生产一种以抛物线y²=4000x绕X轴旋转而成的4m微波天线抛物面板，需要先制造一块检验样板，允许最大制造误差δ_允=0.03mm。现准备按样板轮廓编程，在数控铣床上加工，采用等插补段直线逼近法确定步长l_插及计算各插补节点坐标的步骤如下：

1）求最小曲率半径R_min：将方程y²=4000x改写为x=y²/4000，对y连续求导如下：

x′=y/2000，x″=1/2000，x‴=0，代入式3（x″）2x′-[1+（x′）2]y‴=0，得y=0（实际上，根据抛物线的特点，顶点处的曲率半径肯定最小，可不必进行上述计算），再将y=0代入式

R=[1+（x′）2]³/2/x″

得R_min=2000。

2）计算最小曲率半径处的允许插补长度l_插。

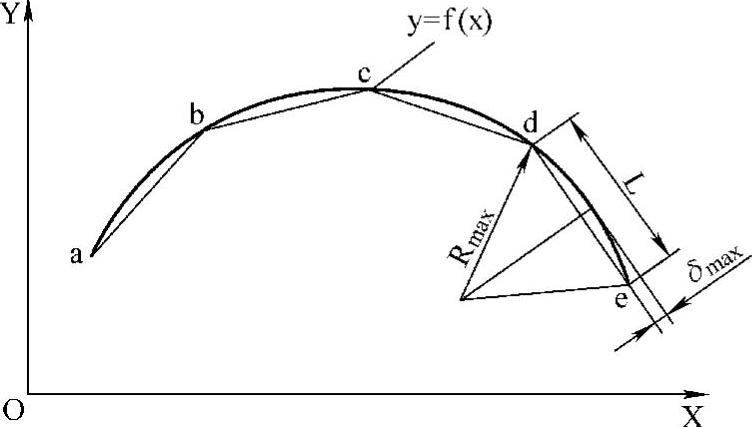
图3-7 等插补段直线逼近法

考虑实际加工时的系统误差，其插补误差Δ_插应小于δ_允，故公式

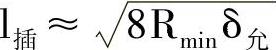
将δ_允用Δ_插代替，即

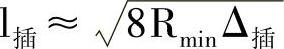
现设定Δ_插=0.01，则

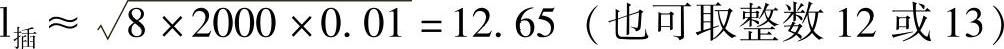
3）求插补节点的坐标：解联立方程

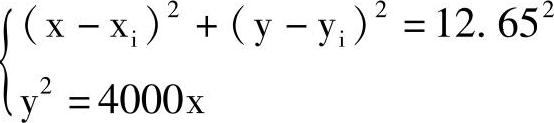
其中，i=0，1，2，3，…；且x₀=0，y₀=0。因样板只需要取抛物线的一侧，故只取x_i≥0，y_i≥0。

4）按上述步骤编程序在计算机上求解，至2000<y_i≤2020止。在程序中用变量（或参数）代替i循环计算节点，然后以直线插补方式编制加工程序。如果要用圆弧插补方式编程，可把圆弧的型值点作为曲线的节点进行圆弧插补。

图3-8 等插补误差的计算

（3）等插补误差法 该方法是使各插补段的误差相等，而插补长度不等，可大大减少插补段数，这一点比等插补段法优越。它可以用最少的插补段数目完成对曲线的插补工作，故对大型复杂零件的曲线轮廓处理意义较大。

设曲线方程为y=f（x），允许插补误差为δ_允，则用等插补误差法求节点坐标的步骤如下（见图3-8）：

1）以曲线起点（x₀，y₀）为圆心，δ_允为半径，建立圆方程为(www.xing528.com)

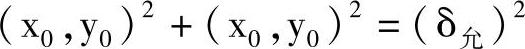
2）求该圆与曲线y=f（x）的公切线方程y=Kx+b。其公切线的斜率

K=tanα=（Y₁-Y₀）/（X₁-X₀）

上式中的X₁、Y₁与X₀、Y₀可通过解下列方程组求得。

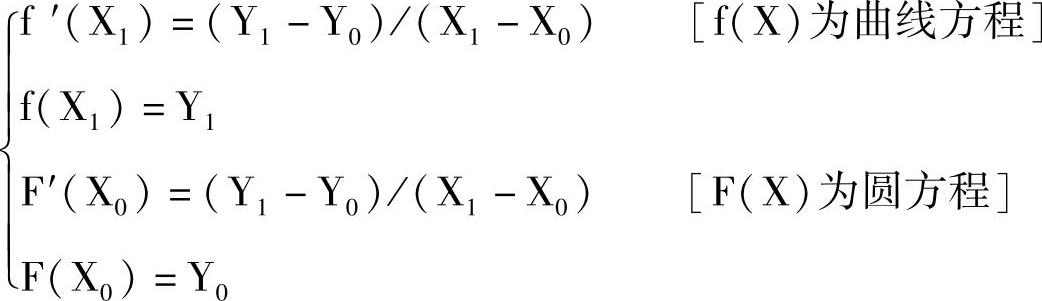
当求出X₁、Y₁与X₀、Y₀后，就可以得到斜率K，从而求得通过点（x₀，y₀）且斜率为K的直线方程。

y=K（x-x₀）+y₀

3）求插补节点：解下列方程组

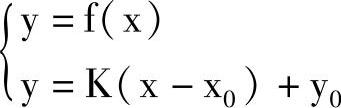
便可以求得交点（x₁，y₁），从而确定第一个插补节点。如再以（x₁，y₁）点重复上述计算，便可得到第二个插补节点坐标，依次逐步计算其余各插补节点坐标值，直到满足加工需要为止。但这一手法用手工计算比较麻烦，用计算机计算要方便得多。

上述三种方法除用于直线插补加工由数学方程表达的非圆曲线外，也常用于圆弧插补加工此类非圆曲线轮廓时事先在曲线上获取型值点，目的是防止取点的盲目性及控制插补误差。

2.圆弧逼近法

用圆弧逼近曲线有曲率圆法、三点圆法和相切圆法等方法。三点圆法是通过已知三个节点求圆，并作为一个圆程序段。相切圆法是通过已知四节点分别作出两个相切的圆，编出两个圆程序段。这两种方法都应先用直线逼近法求出节点，再求出各圆，编出两个圆弧程序段。

（1）用三点圆法求各段圆弧的圆心与半径 其步骤如下：

1）通过三点P₁（x₁，y₁）、P₂（x₂，y₂）、P₃（x₃，y₃）作圆，如图3-9所示。圆的方程用行列式表示为

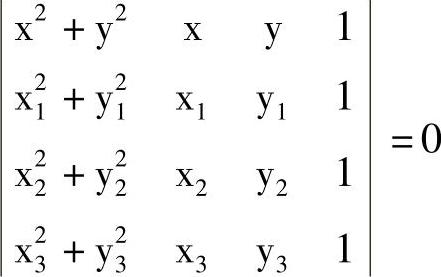
2）求圆心坐标。将圆的行列式方程化为下列形式：

x²+y²+Dx+Ey+F=0

则圆心坐标为

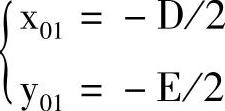
3）求半径R：

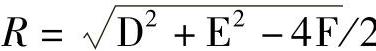
在实际应用中，往往希望以最少的圆弧段来逼近曲线，因此在使用三点圆法时不一定非用邻近的三点，也可用相间隔的三点来作，如图3-10所示。先用P₁（x₁，y₁）、P₅（x₅，y₅）、P₉（x₉，y₉）作一圆，再将其他中间各点的x坐标（或y坐标）代入该圆方程，计算出相应各点的y坐标（或x坐标），与原节点坐标值比较，若差值小于δ_允，则可认为逼近成功，否则要重新选点再做比较。为了防止选点的盲目性，提高工作效率，可以先求各节点处的曲率半径。因为对一个圆来说，其圆上各点的曲率半径相等，所以只有当某段曲线上各节点处的曲率半径相近时，才有可能近似地达到共圆。此外，在圆弧逼近时，也要尽量使相邻各圆弧段之间相切（实在做不到时，也可用小直线段将相邻两圆弧相切过渡）。

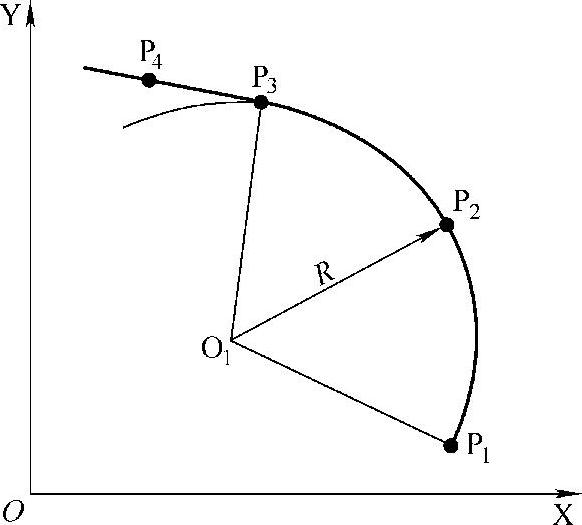
图3-9 用邻近三点求圆

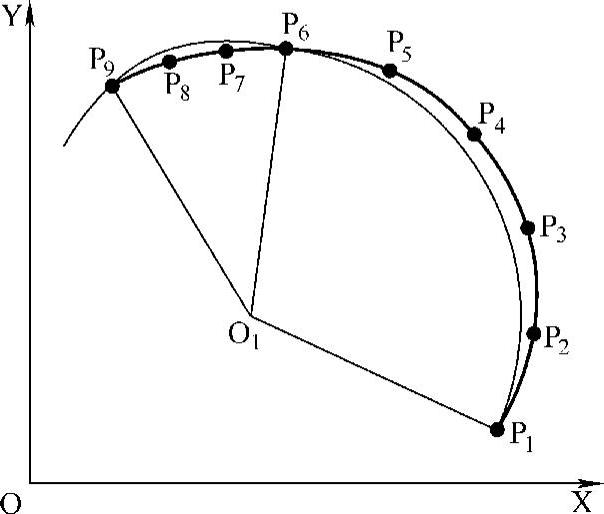
图3-10 用间隔三点作圆

（2）曲率圆法 这是一种等误差圆弧逼近的方法，其计算步骤（图3-11）如下：

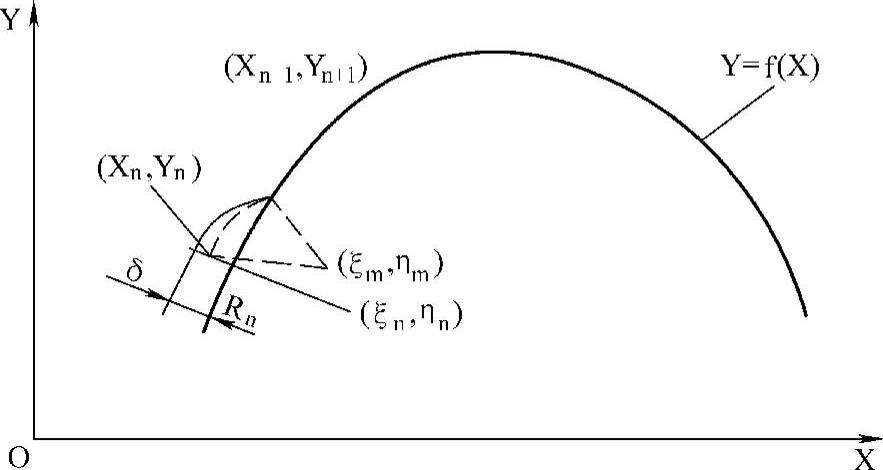
图3-11 曲率圆法

1）以曲线Y=f（X）的起点（X_n，Y_n）开始作曲率圆，其曲率参数为圆心：

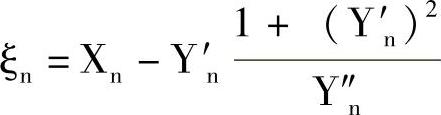
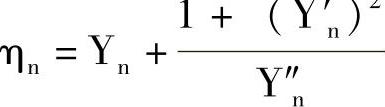
半径：

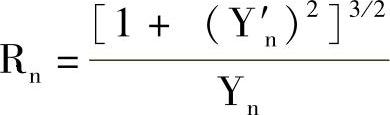
2）已知允许误差δ，求偏差圆与曲线的交点，解联立方程：

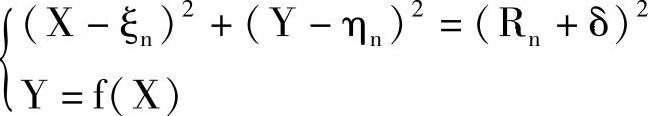
得（X_n+1，Y_n+1）。

3）求过（X_n，Y_n）和（X_n+1，Y_n+1）两点，半径为R_n的圆的圆心坐标，即求

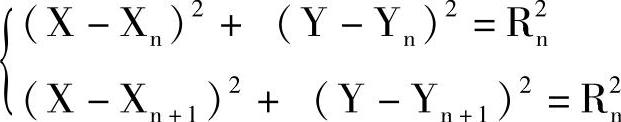
的交点（ξ_m，η_m），该圆即为逼近圆，其起点为（X_n，Y_n），终点为（X_n+1，Y_n+1），半径为R_n。以这些参数编制圆弧程序段。

4）重复上述步骤，依次计算其他逼近圆。