分析组播吞吐量：组播容量

下面运用第3章的引理3.8来分析组播容量。

（1）当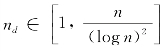且

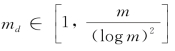
在这种情况下，Pa N采取Mp，SaN采取Ms。首先，有：

引理7.13

在阶段（或阶段），主网（或次网）高速公路的速率均可达Ω（1）。

证明　我们将分为两个部分来证明。

第一部分：分析主网高速公路。重申表示所有参与主网高速公路阶段的主节点集合。考虑PaN中的任意在时隙被调度的链接，其中，。从而，位于相邻的主网渗流格子中。

第一步，导出所有属于的主节点在上产生的干扰总和的上界。用表示这个干扰总和。在8个最近的格子中的发射点与的距离至少为lp，即。接下来，次近的16个格子与之的距离至少为4 lp。扩展到整个区域来看，干扰总和可被界定为

因为α＞2，有≤8P·Δ3（α），其中，Δ3（α）是一个依赖于α的常数。

第二步，给出在时隙τ次网节点对产生的干扰总和（记为）的上界。以为中心的渗流保护区由9个次网渗流格子（SP-C）组成。因此，在任何时隙τ，9个SP-C中至少存在一个格子（记为cτ）本来将被调度（如果它不在保护区内）。考虑包含中节点的格子，所有位于距离cτ最近的8个格子中的次网节点与的距离至少为ls，即。因此，干扰总和可被界定为

因此，可以得到≤8P·Δ4（α）.

其中，Δ4（α）是一个依赖于α的常数。

第三步，给出信号强度的下界，记为。因为任意直接的通信对都是位于相邻格子中，所以，。因此，信号的强度满足：

最后，考虑SINR的极限。我们有：

其中，R1＞0是一个常数。因为中每个发射点在连续9个时隙中必然至少被调度一次。从而，主网高速公路的速率至少可达。

第二部分：分析次网高速公路。对SaN中的任意链接，如果在渗流保护区之外，则它可能被服务到。然而，可能存在一个时隙τ0，其中一个主网节点距离次网节点太近了以至于在上施加了破坏性的干扰。调度机制可以防止这种情况发生。对于SaN，同一个数据包将被连续发3次，从而，可以保证这3个时隙中至少有一个在其中所有的与的距离最小为。因此，

从而，＜8P·Δ3（α）+2α·P。

与第一部分类似，得到，＜8P·Δ3（α）。而且，

则有，。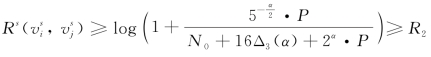

其中，R2＞0是一个常数。因为的发射点在27个时隙中至少能被成功调度一次，所以，次网高速公路的速率可达。

结合两个部分的分析，得证此引理。

下面，将逐个阶段地分析吞吐量，并根据引理3.9，得到最终的可达吞吐量。为了简洁化分析，首先定义一些表达式。在考虑PaN中的第k个组播会话，用表示的欧几里得生成树的有向边集合，即对所有，

在考虑SaN中的第k个组播会话时，关注的是而不是，从而，对所有的，定义，其中，是服务集。重申事件表示组播在第j阶段、在路由机制下，经过节点vi（第3章）。在以下的分析中，为了简便，我们将用表 示；用E（j，k，i）表示。

在高速公路阶段，得到以下结论：

引理7.14

在阶段（或阶段），主网（或次网）的组播吞吐量可达。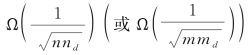

证明　针对PaN的结果进行分析，然后将其扩展到Sa N的情况。根据引理7.13，所有主网高速公路上的站点在阶段，皆可维持常数速率，即=Ω（1）。根据引理3.8，只需要证明所有主网高速公路站点的充分区域面积不超过。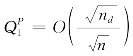

考虑一个主网高速公路站点。

首先，分析事件E（1，k，t）。对任意eij∈∏k，定义事件Eij（1，k，t）：在阶段，从ui到uj的路由通过站点很明显有，Pr（E（1，k，t））=。由联合界（union bounds），则有：

其次，给出Pr（Eij（1，k，t））的上界。考虑ui→uj在阶段的路由，定义数据被水平（或垂直）传输的距离为水平（或垂直）跨越距离，记为（或）。从而有：

其中，节点ui，j由算法7.1确定，hp=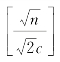且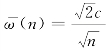·（κlog hp-）+1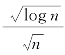）+。考虑一个面积为wp×的矩形区域（其中wp表示条的宽度），则有：

最后，给出的一个上界为：

通过引理3.3，我们有：

因为‖uiui，j‖+‖ui，juj‖≤‖uiuj‖，所以，(https://www.xing528.com)

由于nd=O（n/（logn）2），即=Ω（ndlogn/n）。从而，=O（）。因此，证得PaN的结果。运用类似的过程，可以得到SaN的结果。

下面，分析连通路径阶段：阶段（或阶段）。

引理7.15

在阶段（或阶段），主网（或次网）的组播吞吐量可达（或）。

证明　运用与引理7.13类似的过程，可以证明在阶段（或阶段），主网或次网连通路径均可维持常数速率。因此，只需证明（或）的充分区域面积至多为（或者）。

第一部分（对PaN）：给定一个主网节点，，首先考虑事件E（2，k，t）。对于eij∈∏k，定义Eij（2，k，t）为：在阶段，ui→uj的路由经过节点。从而，则有：

接下来，考虑Pr（Eij（2，k，t））的上界。在ui→uj的路由的阶段，记数据传输的水平和垂直方向最大的距离分别为，则有：

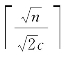其中，hp=且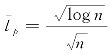。考虑一个大小为的长方形区域，有。进而，

因此有：

最后，可以选择，从而得证此引理。

第二部分（对SaN）：与第一部分的重要不同是：路径由于保护区的拦阻而不能直接水平或者垂直延伸。路径需要沿着保护区的边界绕行，这将增加数据的传输距离和一些点的充分区域的面积。只要证明对所有而言，其充分区域的面积的阶不会增加即可。对于任意次网节点，首先考虑事件Es（2，k，t）。定义事件为：ui→uj的路由在阶段通过了节点。接下来，将构造区域使得

以包含的次网连通格子为中心，区域的大小为3·μ·×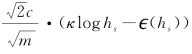。从而，可得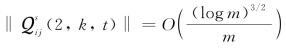。根据引理7.8，我们可得，从而完成此引理的证明。

结合引理7.14和引理7.15，我们得到

定理7.4

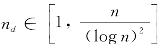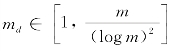当且，PaN和SaN的每会话可达组播吞吐量分别为Ω（f2（n，nd））和Ω（f2（m，md））。

（2）当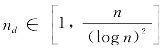且

在这种情况下，PaN采取Mp，Sa N采取。在阶段，可以让SaN闲置，这样不会改变吞吐量的阶。因此，在阶段，Pa N的吞吐量不会小于前面的情况。在阶段，Sa N运行机制，运用类似于引理7.15的方法，可以证明对PaN中的传输产生的干扰不会超过产生的干扰。基于以上的分析，可得到：

引理7.16

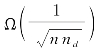在阶段，主网的组播吞吐量可达；在阶段，主网的组播吞吐量可达。

下面，分析SaN的组播吞吐量。

引理7.17

次网SaN的组播吞吐量可达Ω（f2（m，md））。

证明　我们只需证明对任意，其充分区域的面积的上界为

定义事件为：在阶段，通过节点。对任意eij=uiuj∈∏k，定义事件为：在机制下，ui→uj的路由通过节点。下面，我们构造区域使得

与引理7.15的第二部分类似，必须使路由路径绕过保护区的阻拦。因此，构造区域为：以包含的次网连通格子为中心、大小为3·μ·的矩形区域。所以，则有：

根据引理3.3，我们有：

从而，得证此引理。

定理7.5

当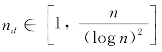且，PaN和SaN的每会话可达组播吞吐量分别为Ω（f2（n，nd））和Ω（f2（m，md））。

（3）当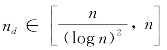

在这种情况下，Pa N采取，Sa N采取。运用与上述类似的分析过程，可以得到：

定理7.6

当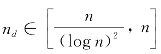，PaN和Sa N的每会话可达组播吞吐量分别为Ω（f2（n，nd））和Ω（f2（m，md））。