服务集合分析：如何优化您的业务？

下面开始分析服务集并证明以下引理。

引理7.6

针对SaN的服务集（定义7.3）的势趋向于ms，即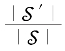→1，且对所有一致以高概率有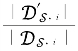→1，as n，m→∞。

（1）未被服务格子总面积

基于引理7.1，提出一个引理来证明所有保护区的簇的大小是有限的。

引理7.7

当时，任意保护区（包括渗流保护区和连通保护区）的簇至多包含μ个保护区。

证明　考虑泊松布林模型，其中，r=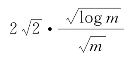且λ=n。因为当λ0·=λ·r2时，关联图。因此，等价于，其中，r0=1且λ0=8n·。因为，我们有λ·r2＜pc。根据引理7.1，所有圆盘的簇的大小至多为一个常数μ。因为一个半径为r/2的圆盘能将一个保护区完全包含，所以所有保护区的簇的大小亦不超过常数μ。

引理7.8

非服务格子的总面积，记为S（m），至多为9·μ·n·，其中，常数μ表示最大保护区簇中包含保护区的数量。

证明　对任意大小为μi的簇，存在一个边长为的正方形能够完全包含所有这μi个保护区以及它们可能包围的非服务格子。因此，这μi个保护区导致的非服务格子的总面积，记为S（m，μi），满足S（m，μi）≤9·。从而，非服务格子总面积满足S（m）≤，其中，Smax是以下优化问题的最优解：

很容易导出，从而，完成引理证明。

（2）当md=ω（log ms）

对于这种情况，根据定义7.3，服务集定义为。从而，有。注意需要假设7.2的条件n=o（m/log m）。

引理7.9

下式以高概率成立：，其中，→0，as m→∞。

证明　定义一个随机变量，其服从期望为≤ms·Smax=9·μ·ms·的泊松分布。根据引理3.2契诺夫界（Tails of Chernoff Bound），我们有

因为n=o（m/log m），得证=o（1）。

根据引理7.9，可得到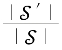→1。下面，针对所有的，导出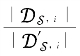的一致上界。首先估计。

引理7.10

对所有的，以高概率有成立，其中，=o（1）。(www.xing528.com)

证明　对每一个，定义一个随机变量。根据引理7.8，服从一个泊松分布，其期望值至多为9·μ·md·n·。根据引理3.2，我们有：

因此，当md=ω（log ms）时，有=o（1）。

由引理7.10，得到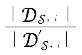→1，as n，m→∞。

结合引理7.9和引理7.10，得证引理7.6针对md=ω（log ms）的情况。

（3）当md=O（log ms）时

对于这种情况，根据定义7.3，服务集定义为

与md=ω（log ms）时的情况不同，需要假设7.2中新的假设条件n=。首先给出以下引理。

引理7.11

对所有的，有。

证明　根据的定义，对所有的.因为，所以。因此，。

根据引理7.11，有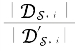→1。下面考虑的势。首先，显然成立。

引理7.12

下式以高概率成立：，其中，=o（1）。

由于n=，有→0。从而，得证此引理。

依据引理7.12，有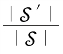→1，as n，m→∞。

结合引理7.11和引理7.12，得证引理7.6针对md=O（log ms）的情况。

（4）服务集合的意义

下面讨论服务集的作用。根据提出的路由机制，只有源节点属于服务集的组播才会被考虑，且对每个考虑到的组播，只有属于的目的节点才会被考虑。因此，根据引理7.6，如果可以证明Sa N中每个源节点为的组播会话可以λ的速率将数据传输到中的所有节点上，就可以说Sa N的组播可达吞吐量为λ。因此，很明显，服务集就是发挥着定义7.1中的作用。