【摘要】:与之相应,为Sa N设计了专门的渗流机制和连通机制。根据nd和md值的不同选取较好的机制,结果如表7-1所列。表7-1可达网络组播量假设7.2对于m,md和n,1)当md=ω时,我们假设n=。基于一种称为Arena的方法,Keshavarze-Haddad等[69,71]推导出密集网的组播容量的一个上界如下:定理7.2PaN的每会话组播容量的上界为用m和md代替上式中的n和nd,可得针对Sa N的类似结果。定理7.3SaN的组播吞吐量为Cs:注意定理7.3中,对Sa N而言,md不能覆盖到其整个区域[1,m]。
为了描述方便,首先定义两个函数如下:
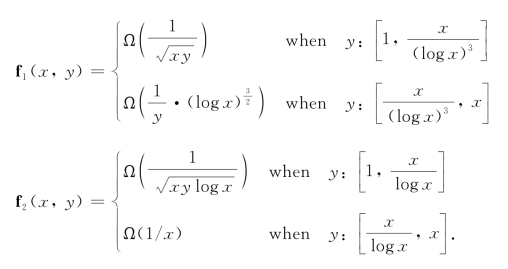
对于Pa N,可采用两种类似于[71]中的路由机制:渗流机制(P-S)和连通机制(C-S)。与之相应,为Sa N设计了专门的渗流机制和连通机制。根据nd和md值的不同选取较好的机制,结果如表7-1所列。
表7-1 可达网络组播量

假设7.2
对于m,md和n,
1)当md=ω(log m)时,我们假设n=![]() 。
。
2)当md=O(log m)时,我们假设n=![]() 。
。
定理7.1
在假设7.2下,Pa N和Sa N的可达组播吞吐量的阶如表7-1所列。
根据定理7.1,保证了SaN的出现不会影响到PaN的吞吐量阶。(https://www.xing528.com)
基于一种称为Arena的方法,Keshavarze-Haddad等[69,71]推导出密集网的组播容量的一个上界如下:
定理7.2
PaN的每会话组播容量的上界为
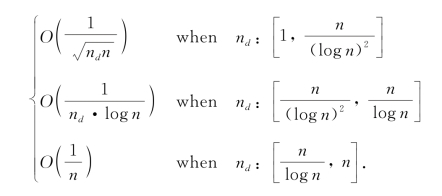
用m和md代替上式中的n和nd,可得针对Sa N的类似结果。
结合[69,71]给出的组播容量上界,得到对于一些区域SaN的容量界为紧的。
定理7.3
SaN的组播吞吐量为Cs(m):
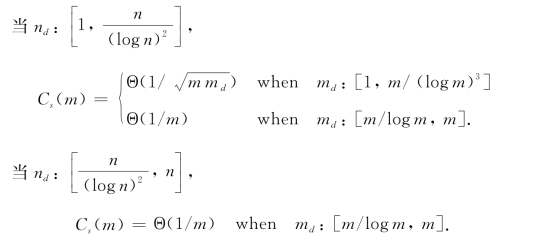
注意定理7.3中,对Sa N而言,md不能覆盖到其整个区域[1,m]。在这些未提及的区域中,仍旧存在上下界之间的差距,如表7-2所列。如何填补这些差距,是一个具有挑战性的问题。
表7-2 SaN容量界不紧的区域

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




