提高聚合吞吐量的方法与技巧

（1）单一链接长度机制下的可达吞吐量

首先根据机制的第一步，选择的传感器数量至少为Ψ·n，从而有：

引理6.18

在机制下导出的吞吐量是Ψ-可达的。

定理6.8

针对DPC-AFs，在设定N=的聚合机制下，聚合吞吐量可达：

其中，

（2）复合链接长度机制下的可达吞吐量

首先有：

引理6.19

在机制下导出的吞吐量是Ψ-可达的。

该引理可通过以下这个引理和引理3.2证明。

引理6.20

考虑n个随机变量Xi∈｛0，1｝，令p=Pr（Xi=1）且令X=。从而有：

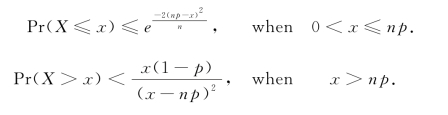
定理6.9

针对DPC-AFs，在设定的聚合机制下，聚合吞吐量可达：

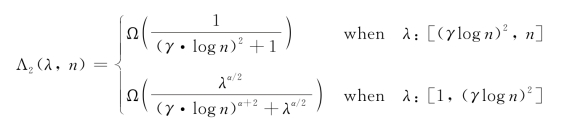
其中，(https://www.xing528.com)

（3）聚合吞吐量和汇集效率间的权衡

基于定理6.8和定理6.9，则得到：

定理6.10

在聚合机制下，针对DPC-AFs，最优的可达聚合吞吐量记为Λ Λ（λ，n），最优聚合吞吐量和汇集效率间的权衡记为Φ：=Φ（λ，n），则有：

●当Ψ（n）=（1-ε9）·或者Ψ（n）∈（0，（1-ε9）·]时，有Φ=Λ=Ω（1）对任意λ：[1，n].

●当Ψ（n）-（1-ε9）·时，有：

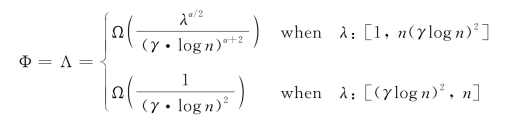
其中，γ=。

●当Ψ（n）-（1-ε9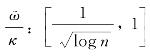）·时，有：

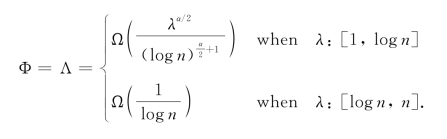
在两个机制下的具体权衡值如表6-1所列。

根据定理6.10，有以下的结论：

●单一链接长度机制是不可扩展的。

●在复合链接长度机制下，当Ψ（n）=（1-ε9）·时，Ψ-可达吞吐量阶为Θ（1），这意味着复合链接长度机制实际上是可扩展的。给出一组满足表6-1中条件的可行常数：

因此，设定ε9=2×104，这意味着0.92-可达吞吐量阶是Θ（1）。

●当时，机制下的权衡要好于下的权衡，如图6-9（d）所示；此外针对其他情况，则前者不比后者好，如图6-9（a）—图6-9（c）所示。

图6-9　最优权衡