聚合容量下界优化方案

通过设计聚合机制，来给出随机扩展WSN的聚合吞吐量。

（1）针对一般Divisible聚合函数的聚合机制

聚合机制AN，n依赖于机制网格（定义3.7）L1=L（，0）。为了描述方便，假设总是一个整数，这对最终结果的阶不会产生影响。以左上角的格子为原点（0，0），依照从左到右、从上到下的顺序给每个格子一个二维坐标，即右下角格子的坐标为（δ，δ），其中δ=δ（n）=。依据VC定理（引理4.2），我们有：

引理6.3

对机制网格L1中的任意格子（i，j），其包含的节点数目ni，j以高概率满足

首先给出聚合路由机制。该聚合路由树分为两个层次：聚合骨干链接和局部聚合链接。

聚合骨干：从L1中的所有格子（除了包含s0的格子）中随机选取一个传感器，得以组成一个（δ+1）2-1个点的集合，记为，并定义作为骨干集合。中的所有点被称为聚合站点，或者为了简便，直接称之为站点。

假设sink节点s0位于格子Cδ，δ：（δ，δ）中。通过连接相邻的同一行的站点构成水平聚合骨干；连接第δ列的站点，构成垂直骨干，如图6-3（a）所示。对于sink节点s0处在其他一般位置的格子Ci，j：（i，j）的情况，构建路由的不同之处在于我们连接第j列的站点构建垂直骨干，如图6-3（b）所示。事实上，可以构建一条从格子Cδ，δ到格子Ci，j的多跳的路径，如图6-3（c）所示。可以证明，聚合机制的瓶颈不会出现在这样的路径上，也就是说，sink节点s0的位置不会影响结果的阶。

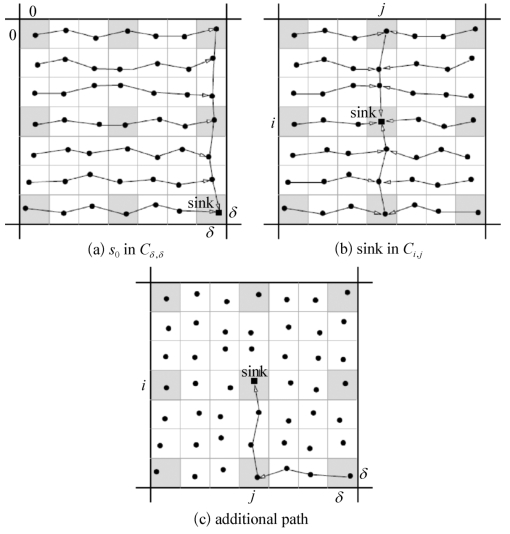
图6-3　针对一般divisible函数的聚合路由骨干

局部聚合链接：在L1中的所有格子中，除了sink节点s0之外，所有传感器都通过一个单跳与s0通信，如图6-4（a）所示。

图6-4　针对一般divisible函数的局部聚合

下面考虑聚合调度机制。与路由机制相对应，调度机制也分为两个阶段：局部调度和骨干调度。在第一个阶段，每个格子中的传感器上的测量值将被聚合到聚合站点上；在第二个阶段，聚合站点上的聚合值将被逐层聚合到sink节点上。

局部聚合调度：在此阶段，用一个4-TDMA机制调度L1中的格子，如图6-4（a）所示，只有完全包含在格子中的链接才被调度。这样的链接在每个格子中的数目以高概率不超过8logn。从而，可以进一步把4-TDMA机制的每个时间片分为8logn等分的子时间片，保证所有的局部链接在32logn个子时间片内可以被调度一次。

骨干聚合调度：在此阶段，数据将以流水线的方式被聚合到sink节点上。骨干调度分为两个阶段：水平骨干阶段和垂直骨干阶段。

在水平骨干阶段的初始状态，每个格子Ci，j中的聚合站点bi，j存储着来自其包含的节点的N轮测量值（可用一个矩阵表示）的聚合函数值。记这N个聚合函数为

至此，可用一个矩阵来表示（δ+1）2个站点拿到的N轮数据。在水平骨干阶段，记bi，j以及它的所有后继点为，从而有=Θ（（j+1）·logn），则bi，j上的第k轮数据的聚合值为

其中，，for k=1，2，…，N.

在垂直骨干阶段的初始状态，所有的站点bi，δ存储着N个基于站点bi，j，0≤j≤δ的数据的聚合函数值，可记为，1≤k≤N。至此，可用一个矩阵来表示δ+1个站点拿到的N轮数据。记bi，δ以及它的所有后继点为，从而有。在垂直骨干阶段，bi，δ上的第k轮数据的聚合值为

其中，，for k=1，2，…，N.

采用一个9-TDMA机制调度水平骨干，如图6-3（a）所示，并用一个3-TDMA机制调度垂直骨干。设计算法6.1和算法6.2来调度水平和垂直骨干聚合。两个算法每依次运行一次，在sink节点上就可得到N轮测量值的聚合值。在表述算法之前，定义两个集合序列：

对h=0，1，2和v=0，1，2，定义

对h=0，1，2，定义

下面分析聚合容量。由于聚合机制是分层次的，所以将逐个分析。

局部聚合阶段吞吐量：在此阶段，因为可以保证所有的局部链接在32logn个子时间片内可以被调度一次，则以下引理成立。

引理6.4

在局部聚合阶段，如果每个被调度的链接可以达到速率为R1（n），则每条边可以维持的平均速率为，因此，完成N轮的局部聚合至多需要的时间为

在局部聚合阶段，当不引入block coding技术（将在后面介绍）时，所有被传输的数据都是原始的测量值，而不是聚合过的数据，所以这个阶段的吞吐量与具体的聚合函数无关。首先给出R1（n）的阶。

引理6.5　局部链接速率

在局部聚合阶段，被调度的链接速率可达：

证明　采用如图6-3（b）所示的4-TDMA机制调度，运用与引理3.20类似的证明方法，可以得证此结论。需要指出，与引理3.20不同，这里不是平行调度。

因此，结合引理6.4和引理6.5，我们可以得到：

引理6.6　局部聚合调度时间

在局部聚合阶段，当不采用block coding时，完成N轮测量值的局部聚合需要的时间为

骨干聚合阶段吞吐量：我们首先考虑水平骨干阶段。

引理6.7

在水平骨干阶段，如果每个被调度的链接可以达到速率为，则每条边可以维持的平均速率为。

证明　根据算法6.1，每条水平骨干可以在3×3×（N+δ（n）-3）时间内被调度至少N次，因此，可以得证此结论。

下面考虑。运用类似于引理6.5的方法，可以得到：

引理6.8　水平骨干速率

在水平骨干阶段，被调度的链接速率可达：

从而有下面引理。

引理6.9　水平聚合调度时间

在水平聚合阶段，完成N轮数据的水平聚合需要的时间为

其中，(www.xing528.com)

且是函数的值域。

证明　在此阶段，站点bi，j上的第k轮数据的聚合函数值为

因为block coding技术没有被采用，从而，站点bi，j的负载为

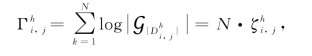
因此，在水平骨干阶段，完成N轮数据的水平聚合需要的时间至多为

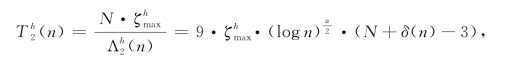
我们可以得证此结论。

下面用类似于水平阶段的过程来分析垂直骨干阶段。

引理6.10

在垂直骨干阶段，每个被调度的链接可达到的速率为，则每条边可以维持的平均速率为

证明　在此阶段，3-TDMA机制被采用。运用类似于引理6.5的方法，可以得到=Ω（（logn）-α/2）。根据算法6.2，每条水平骨干可以在3×（N+δ（n）-3）时间内被调度至少N次，因此，可以得证此结论。

引理6.11　垂直聚合调度时间

在垂直聚合阶段，完成N轮数据的水平聚合需要的时间为

其中，

且是函数的值域。

证明　在此阶段，站点bi，δ上的第k轮数据的聚合函数值为

因为block coding技术没有被采用，从而，站点bi，δ的负载为=N·。因此，在垂直骨干阶段，完成N轮数据的垂直聚合需要的时间至多为

从而可以得证此结论。

根据定义6.1，得到以下结论：

定理6.1

在设定N=的聚合机制AN，n下，聚合吞吐量可达：

其中，的定义分别在引理6.9和引理6.11。

证明　首先，考虑N轮测量值的总的调度时间T（AN，n），则显然有且聚合机制AN，n下的聚合吞吐量的阶为

基于引理6.9和引理6.11，对N=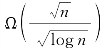，即N=Ω（δ（n）），则有：

结合引理6.6，我们可以证明此结论。

根据以上的分析，将依赖于具体的聚合函数类别。下面将定理6.1的结果应用到一个特殊例子：divisible perfectly compressible函数。

（2）针对Divisible Perfectly Compressible聚合函数的吞吐量

根据divisible perfectly compressible聚合函数（DPC-AF）的特点，通过定理6.1我们得到，

定理6.2

针对DPC-AFs，在设定N=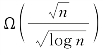的聚合机制AN，n下，聚合吞吐量可达：

证明　根据引理6.1，对于DPC-AFs，有

类似地，=O（log m）。由于m=Θ（1），利用定理6.1得证此定理。

（3）针对Type-Threshold DPC-AFs的聚合机制

由于感知的测量值是周期性产生的，从而函数值需要重复的计算。因此，这里就使得引入block coding技术成为可能[93]。Block coding技术通常会结合连续的函数计算。这种技术能够显著地提高type-threshold函数在同位网络中（collocated network，其干扰图为一个完全图）的吞吐量。给定一轮测量值，记为一个n维的向量，max、min、range和indicator等函数都属于type-threshold函数。首先介绍[93]中的一个结论（[93]中的定理4）。

引理6.12

在协议模型下，一个同位网络针对type-threshold函数的聚合容量为Θ（1/logn）。

在我们的机制AN，n下，在每个格子中，子图的通信图可以看做是一个具有Θ（logn）个顶点的同位图，任意两条边都不能同时调度。从而，这就有可能通过将block coding技术引入AN，n中得以提高系统的吞吐量。要解决的主要问题是如何将引理6.12的结果扩展到一般物理模型下。分析一下引理6.12的证明过程：令N=Θ（n），假设每个成功的传输都可达到常数的速率，并证明需要O（n logn）个时间片来完成N轮测量值的聚合。因此，由于在聚合机制AN，n下，成功传输的速率为Ω（（logn）-α/2）而不是常数速率，我们有：

引理6.13

在一般物理模型下，通过设定block coding的块长度为Nb=Θ（logn），则局部聚合N=Ω（logn）轮测量值需要耗费时间为

引理6.13成立的条件是N=Ω（logn），这与定理6.1和定理6.2中的条件N=不冲突。因此，可以通过引入block coding技术来修改机制AN，n，记为。最后我们有：

定理6.3

针对DPC-AFs，在设定N=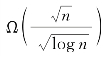的聚合机制下，聚合吞吐量可达

证明　通过引入block coding技术，

则根据定义6.1，可以证明此结论。