系统模型的形式化定义与可达聚合吞吐量

考虑随机WSN的模型为，其中一个传感器被选作sink节点，记为s0。每个节点si，0≤i≤n-1，周期性生成环境的测量值，这些测量值属于一个有限集合，其中，并且关注函数（Functions of Interest）需要重复的计算。直观来看，WSN的聚合容量要依赖于sink节点的关注函数[93，109]。如图6-1所示。

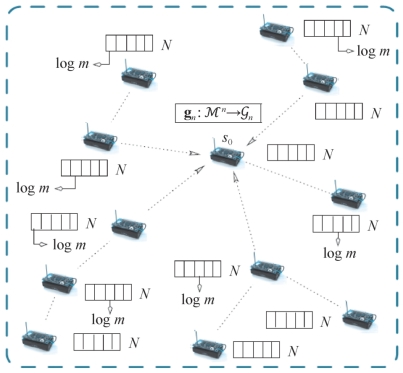
图6-1　系统模型

（1）形式化定义

记sink节点关注的聚合函数为gn：；对任意k，1≤k≤n，定义n个测量值的函数为gk：，其中是函数的值域。假设每个传感器有一个大小为N的数据块作为一个先验的信息。定义所有n个节点上N轮测量值为一个处理单元。在实际应用中，通常只有同一轮的测量值才有需求被聚合。我们首先介绍一些符号。

●用一个n×N的矩阵表示一个处理单元，其中Mn×N（i，j）表示传感器si上的第j轮测量值。

●对于一个k维的向量Mk=[M1，M2，…，Mk]，其中，定义

●给定一个矩阵Mk×N，1≤k≤n，定义

●记一个处理单元为N轮测量值的聚合机制为AN，n，则在AN，n下，输入为Mn×N，sink节点s0上的输出为。

（2）聚合容量定义

首先定义可达聚合吞吐量。以下涉及的log函数均是以2为底。

定义6.1　可达聚合吞吐量

一个吞吐量Λ（n）对函数gn是可达的，如果存在一个聚合机制AN，n可以把任意用时T（AN，n）聚合 到sink节点上得到，其中，。

在具有密集性数据传输需求的WSN中，如多媒体无线传感器网络[154]，聚合吞吐量是尤为重要的系统性能指标。需要指出，如果是移动WSN，对网络吞吐量需要另外的定义。基于可达聚合吞吐量，根据定义2.5可以得到随机WSN的聚合容量。

（3）关注聚合函数（Aggregation Functions of Interest）

本章将主要考虑symmetric（对称）函数，其值与数据分量的顺序（置换）无关：对任意1≤k≤n，对所有的置换σ，有

在实际应用中的许多函数，如许多统计函数，都属于symmetric函数。Symmetric函数体现的是以数据为中心（Data Centric）的函数类别[155-156]。在WSN的应用中，symmetric函数体现的是传感器产生的数据本身比它的来源更重要的理念。进而研究范围限制在一类特定symmetric函数上，即divisible（可分）函数。Divisible函数的特点是可以分而治之（Divideand-Conquer），这种函数通常被作为WSN中数据聚合问题的一般性函数。

下面介绍另外两类特殊的symmetric函数：type-sensitive函数和type-threshold函数。

定义6.2　Type-Sensitive函数

一个symmetric函数gn（·）被称为type-sensitive函数，如果存在一个常数θ，0＜θ＜1，和一个整数n0，使得对n≥n0和，给定任意子集{M1，M2，…，Mi}，将存在两个不同的子集和，使得

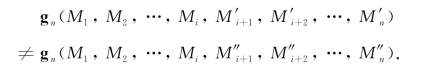
对于一个n维向量，Mn的mode函数（出现次数最多的值），mean函数，median函数，以及standard deviation函数都属于typesensitive函数。

定义6.3　Type-Threshold函数

一个symmetric函数gn（·）被称为type-threshold函数，如果存在一个非负=m维向量ξ，称之为threshold向量，使得对任意Mn∈，有

其中，ϕ（Mn）被称为type向量，定义为ϕ（Mn）=[ϕ1（Mn），ϕ2（Mn），…，ϕm（Mn）]，ϕk（Mn）：=|{si：Mi=k}|；min函数是取元素方式（Elementwise）的最小值。(www.xing528.com)

对于一个n维向量，max函数，min函数，range函数，kth largest值函数，以及indicator函数等都属于type-threshold函数。

特别是，考虑一类重要的symmetric（对称）函数，称之为divisibleperfectly-compressible聚合函数（DPC-AFs）。称一个divisible函数为perfectly compressible（完美压缩），如果来自不同传感器的同一轮的测量值可以聚合成与原先长度相同的新的数据[109]。从而有以下这个引理。

引理6.1　DPC函数的压缩长度

对任意的divisible-perfectly-compressible聚合函数gk，1≤k≤n，有=Θ（m），其中是函数gk的值域。

主要考虑两类特殊的DPC-AFs：type-sensitive DPC-AF和typethreshold DPC-AF。如图6-2所示。

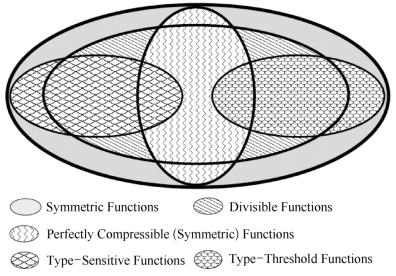
图6-2　聚合函数的类别

直观来讲，对于type-sensitive函数而言，当足够大比例的数据未知时，其值无法确定，而对于type-threshold函数而言，其值可由一定数量的数据来决定。type-sensitive DPC-AF的一个代表性例子是average（平均）函数；type-threshold DPC-AF的代表性例子包括max、min、range以及各种indicator函数。

（4）网络扩展模型

下面讨论随机密集网和扩展网的区别。在标度律的研究中，一般有两种形式的扩展模式：扩展式和密集式。二者在工程意义上的区别主要体现在常见的干扰受限（interference-limitedness）和覆盖/能量受限（coverage/power-limitedness）。密集式网络是密集式的部署，用户收到的信号具有充分大的信噪比（SNR），而网络吞吐量主要受限于同时进行的传输之间的干扰。扩展式网络是相对稀疏式的部署，通信的源点和目的节点的距离不断扩大，网络吞吐量受限于传输能量和干扰。

下面讨论随机网络扩展模式的判断准则。首先，介绍一个关于欧几里得最小生成树的结论[81，95，157-159]。记中n个点的EMST中的最长的边为L（n，a2）。对随机变量L（n，a2），根据[158]中的结果，Li等在[81]中提出了以下引理。

引理6.2　EMST最长边的长度

对于随机变量L（n，a2），对任意实数ν（n），则有：

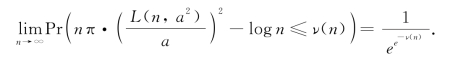
基于引理6.2，令ν（n）=-ln ln n，有L（n，a2）=以高概率（至少1-1/n）成立；令ν（n）=-ln n，有L（n，a2）=O（a·）以高概率（至少1-1/n）成立。从而有：

根据L（n，a2）的长度，即，来定义随机网络（n，a2）扩展模式的判断准则。

定义6.4　扩展模式

给定一个随机网络，如果a·=O（1）以高概率成立，则它是密集式网络，如果a·=ω（1）以高概率成立，则它是扩展式网络。

（5）随机密集WSN和随机扩展WSN的比较

随机密集WSN（RD-WSN）和随机扩展WSN（RE-WSN）是随机密集式和随机扩展式网络的代表性例子。RD-WSN代表的是一种监测区域面积固定，网络的规模随传感器的部署密度的增大而变大；RE-WSN代表的是一种传感器的部署密度固定，网络的规模随部署区域面积的增大而变大。

（6）通信/干扰模型和扩展模型的关系

下面分析常见的通信模型和扩展模型的组合，并为本书选择出最优的模型，即一般物理模型（定义2.4）。

通常将协议模型和物理模型归为固定速率（Fixed-rate）模型（FCM）；将一般物理模型（Gphy M）归为自适应速率（Adaptive-rate）模型（ACM）。

●密集式网络中的FCM：Gupta和Kumar[6]只是针对密集式网络定义了协议模型和物理模型。在密集式网络中，假设所有成功的传输可达到常数速率是合理的，因为充分大的SINR（信噪干扰比）可以达到。因此，[89，93，106，160]中在FCM下取得的聚合容量针对RD-WSN来讲是合理的。

●密集式网络中的Gphy M：在密集式网络中，FCM可以看做是Gphy M的完美的简化。实际上，在二者之下推导的容量是相等的（允许FCM多参数）。

●扩展式网络中的FCM：在扩展式网络中，根据定义6.4，针对（n，a2）的任意路由机制下，都存在一条边的长度为，即ω（1）。从而，这条边的SNR值会太小而不能达到常数阶的速率。也就是说，在随机扩展网中，假设所有成功的传输可达到常数速率是过于乐观和不现实的。

●扩展式网络中的Gphy M：Gphy M可以近似地体现出在扩展式网络中链接速率的连续性，这正是针对扩展网的工作大多都采用Gphy M的原因。