欧几里得算法生成森林优化

将区域分割成ρ≤m个子区域（方形），保证每个子区域中间有一个基站。注意每个子区域可能包含不止一个基站，但是我们仅需要用到中间的那一个。对于一个组播会话，其生成集为，其中是源节点，表示的目的节点的集合。令表示包含在子区域Sι中的的一个子集，其中，且对任意ι1≠ι2有=∅。令，其中，bι表示子区域Sι中心的基站。从而可以基于每个来构造欧几里得生成树（EST），记为，1≤ι≤φk，其中，φk表示一个占位（occupied）子区域数量的随机变量，即至少包含一个中的节点的子区域的数量。对于每个，除了包含源节点的，bι都作为的根节点；对于而言，作为的根节点。

随机变量φk的大小是占位问题[132]的互补问题。假设nd+1个球被随机地放入ρ个盒子（每个球以等概率放入到每个格子）。令表示空格的数量，则φk=ρ-。通过占位定理，φk的分布为

下面将研究φk，k=1，2，…，ns的一致上界。

定义随机变量φmax=maxk{φk}。关于占位问题的界已有大量的研究[133-134]。由于本书只考虑组播容量的可达下界，所以只需要下面这个比较直观的φmax的上界。在针对混合网络组播容量上界的进一步工作中，则需要对下界φmin展开讨论。

引理5.1

针对φmax，以高概率有φmax=maxk{φk}=O（nd，ρ）。

记由所有的组成的森林为，从而，我们有：(https://www.xing528.com)

引理5.2

森林中边的总长度，即‖‖，对任意k，1≤k≤ns，其阶以高概率为

证明　记中顶点的数目分别为。则显然有。根据引理3.3，有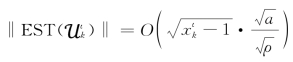。因此存在一个常数κ1使得

通过Cauchy-Schwartz不等式，则有：

因为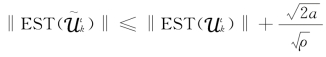，存在一个常数κ2使得

因此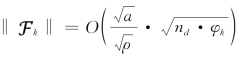，。结合引理5.1，证明此结论。