高速公路系统的建设和管理

将构建高速公路系统（Highway System）以作为组播路由骨干。该系统由两级高速公路系统组成：一级高速公路（First-Class Highways，FHs）和二级高速公路（Second-Class Highways，SHs）。

（1）一级高速公路系统

首先依据文献[68]中的方法构造一级高速公路系统，并介绍传输调度机制使得每条高速公路的容量为常数阶。

构造一级高速公路FH：将基于机制网格构造FH，请如图3-2（a）所示。从而，中共有m2个格子，其中m=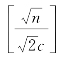。注意，可以调整c的值使得成为一个整数。令表示格子中的泊松点个数，则其服从期望为c2的泊松分布。对任意i，格子非空，即≥1的概率为p≡1-。如果一个格子是非空的，称其为open；否则，称其为closed。基于，生成新的scheme lattice L，如图3-2（a）所示。称中的一条边为open的，如果其跨过的中的格子是open的；称一条路径是open的，如果其只包含open的边。基于一条跨过部署区域的open路径，从对应于该路径的边的格子（中的格子）中随机选取一个点，并将这些点连接起来，就构建了一条一级高速公路。

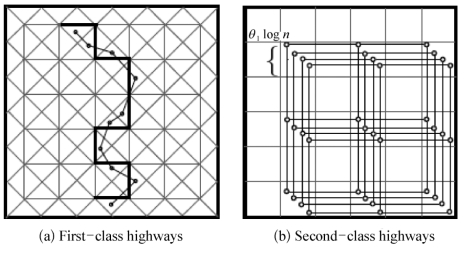
图3-2　构建高速公路

一级高速公路FH的密度：给定一个常数κ＞0，将机制网格分割成水平（或垂直）的矩形块，其大小为m×（κlog m-）（或（κlog m-）×m）个小格子，分别记为。记中不相交的FH的数目为。则有以下结论[68]：

引理3.14　一级高速公路密度

对于满足条件2+κlog（6（1-p））＜0的κ和p∈（5/6，1），存在一个常数δ=δ（κ，p）使得

其中，Nh=，Nv=。

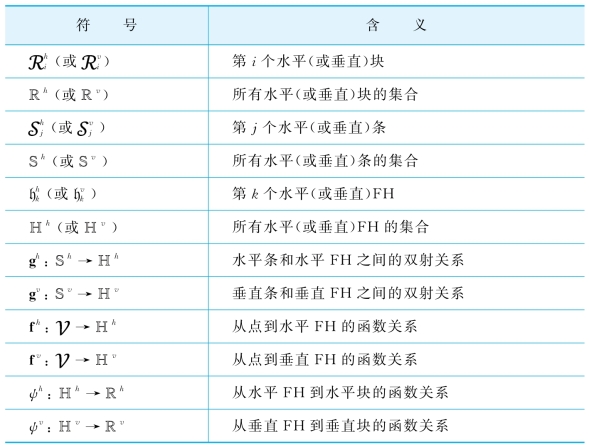
一级高速公路FH的表示：只从每个水平块（或垂直块）中选取δlog m条水平（或垂直）FH，这不会影响到最终结果的阶。可以进一步把每个水平块（或垂直块）分割成δlog m个大小为l×m水平条（或垂直条），其中l=。继而可以开始定义块、条和FH之间的映射，详见表3-2。

表3-2　FH的相关表示

一级高速公路FH的调度：采用一个基于的9-TDMA机制调度一级高速公路，即在文献[68]的图4所示机制中，令K=3和d=1。根据文献[68]中的定理3，每条FH的速率可达Ω（1）阶。

（2）二级高速公路系统

下面构建二级高速公路（Second-Class Highways，SHs）并设计相应的调度机制使得每条SH速率可达Ω（（logn）-α/2）。

构造二级高速公路SH：将基于机制网格构造SH，如图3-2（b）所示，其中，σ＞0是一个常数且我们取＞0为使得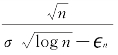为整数的最小数值。这里，=o（1）。从而，有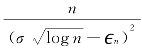个格子。令表示格子中的泊松点个数，则其服从期望为的泊松分布。进而定义的一致下界为。

为确保SH的构造方法可行，给出以下这个引理。

引理3.15　二级高速公路对格子大小的要求

对任意和σ，σ2≥，中的每个格子包含的节点不少于θ1logn个，其中θ1=是一个常数。

可以称的每一行（或每一列）为行块（或列块），并记为。对中的格子进行编号（从左至右，从上至下增序），并称奇数序号（或偶数序号）的格子为奇序（或偶序）格子。用以下步骤在中构造水平（或垂直）SH：首先，从每个格子中选取一个点，然后，水平（垂直）方向连接偶序（奇序）格子中的点构成水平（或垂直）偶序（或奇序）SH。(www.xing528.com)

二级高速公路SH的密度：如果两条SHs没有公共点，则称为不相交的。记中不相交的SHs的数目为。令。根据引理3.15，中每个格子至少有θ1logn个点，从而有：

引理3.16　二级高速公路密度

对任意和σ，σ2≥，存在一个常数θ1=使得

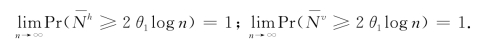
二级高速公路SH的表示：为描述简便，从每个行块（或列块）中只选取θ1logn条水平（或垂直）奇序SH和θ1logn条水平（或垂直）偶序SH。这不会改变最终结果的阶。可以进一步把每个行块（或列块）分割成2θ1logn个大小为的行条（或列条）。进而定义SH，行块和行条之间的映射关系，如表3-3所列。

表3-3　SH的相关表示

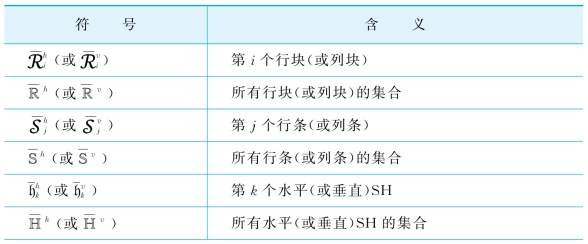
续 表

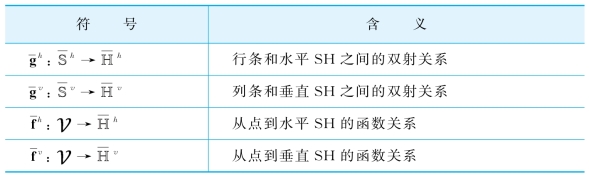
二级高速公路SH的调度：将采用一个16-TDMA机制来调度SHs。设计一个方法叫作并行调度机制：在每个调度时间片（时隙）里，在每个格子中不是只调度一条边，而是同时调度θ1logn条边的发射点，如图3-3所示。

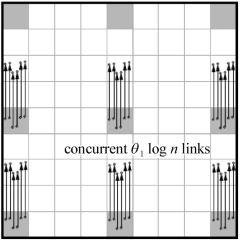
图3-3　二级高速公路的并行调度机制

引理3.17　二级高速公路容量

在并行调度机制之下，每条SH的速率可达Ω（（logn）-α/2）阶。

证明　对SH上的任意一条边，由于其长度至少为，从而其接收点上受到干扰的总和为

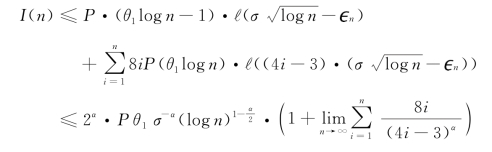
其中，当α＞2时，最后出现的极限是收敛于常数的。另一方面，因为每条边的长度至多为，从而，在接收点上，其信号强度为

所以，SH的速率至少为

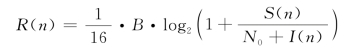
因为α＞2且N0＞0，所以，。因此，R（n）=Ω（（logn）-α/2）。

□