【摘要】：Jacquet和Rodolakis[77]给出了的 上界为O（1/）。Shakkottai等设计了一种新颖的组播路由机制，称之为梳形路由。通过这种机制推导出的结论为：当组播会话的数目ns=nε并且nd=n1-ε，0＜ε＜1，的下界可达Ω（1/）。Li[78]证明了当nd=O时，的阶为Θ（1/），当nd=Ω时，的阶为Θ（1/n）。对于，Li等[70]给出一个下界：当nd=O且ns=，其中，θ＞0是一个正常数，为。本章的工作就将针对，给出上界，并对所有情况ns：（1，n]导出更紧的下界。
Jacquet和Rodolakis[77]给出了（M，D，O）的 上界为O（1/
）。Shakkottai等设计了一种新颖的组播路由机制，称之为梳形路由。通过这种机制推导出的结论为：当组播会话的数目ns=nε并且nd=n1-ε，0＜ε＜1，（M，D，O）的下界可达Ω（1/
）。Li[78]证明了当nd=O（n/logn）时，（M，D，O）的阶为Θ（1/
），当nd=Ω（n/logn）时，（M，D，O）的阶为Θ（1/n）。通过设计一种新颖的工具，称之为Arena，Keshavarz-Haddad和Riedi[71]证明了（M，D，O）、（M，D，Y）和（M，D，G）的上界在nd：[1，n/（logn）2]时为O（1/
），在nd：[n/（logn）2，n/logn]时，上界为O（1/（ndlogn）），在nd：[n/logn，n]时，上界为O（1/n）；并给出了（M，D，Y）和（M，D，G）的下界：当nd：[1，n/（logn）3]时，下界为Ω（1/
），当nd：[n/（logn）3，n/（logn）2]时，下界为Ω（（logn）-3/2/nd），当nd：[n/（logn）2，n/logn]时，下界为Ω（1/
），当nd：[n/logn，n]时，下界为Ω（1/n）。
对于（M，E，G），Li等[70]给出一个下界：当nd=O（n/（logn）2α+6）且ns=
，其中，θ＞0是一个正常数，为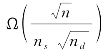
。本章的工作就将针对（M，E，G），给出上界，并对所有情况ns：（1，n]导出更紧的下界。(www.xing528.com)
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
