展开技术的基础知识：线段实长、截交线、相贯线、断面实形等画法几何

展开放样是金属结构制造中放样工序的重要环节，其主要内容是完成各种不同类型的金属板壳构件的展开。要系统掌握展开技术，必须首先掌握求线段实长、截交线、相贯线、断面实形等画法几何知识，这些知识是展开技术的理论基础。

1.求线段实长

在构件的展开图上，所有图线（如轮廓线、棱线、辅助线等）都是构件表面上对应线段的实长线。然而，并非构件上所有线段在图样中都反映实长。因此，必须能够正确判断线段的投影是否为实长，并掌握求线段实长的一些方法。

（1）线段实长的鉴别 线段的投影是否反映实长，要根据线段的投影特性来判断。为此，我们把空间各种线段的投影特性简述如下：

1）垂直线。正投影中，垂直于一个投影面，而平行于另两个投影面的线段称为垂直线。垂直线在它所垂直的投影面上的投影为一个点，具有积聚性；而在与其平行的另两个投影面上的投影反映实长。图2-25所示为三种垂直线的投影情况。

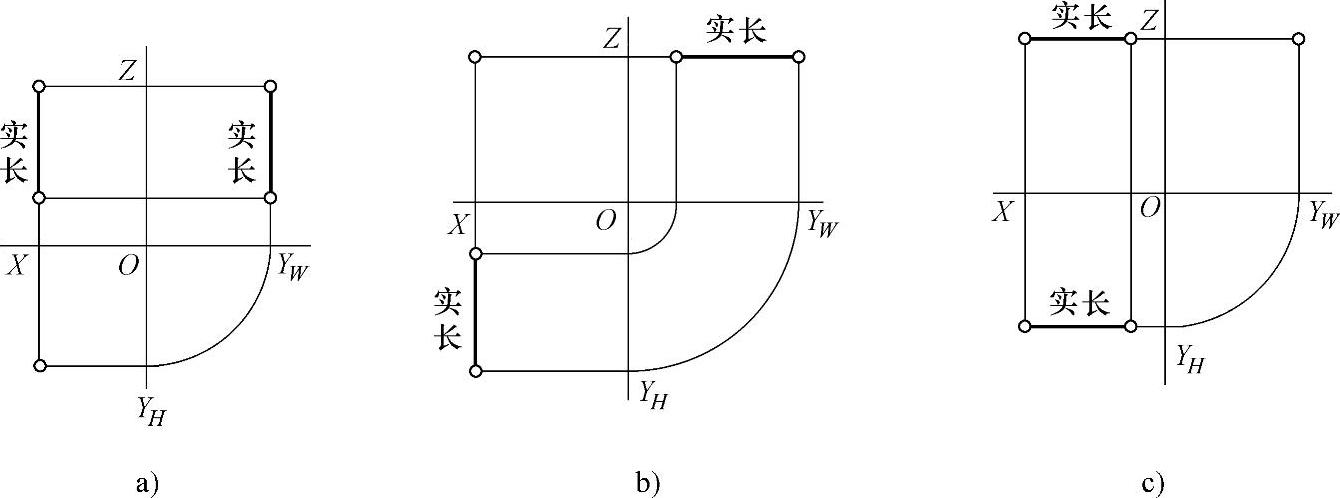
图2-25 垂直线的投影

a）垂直于XOY面的线 b）垂直于XOZ面的线 c）垂直于ZOY面的线

2）平行线。正投影中，平行于一个投影面，而倾斜于另两个投影面的线段，称为平行线。平行线在其所平行的投影面上的投影反映实长；而在另两个投影面上的投影为缩短了的直线段。图2-26所示为三种平行线的投影情况。

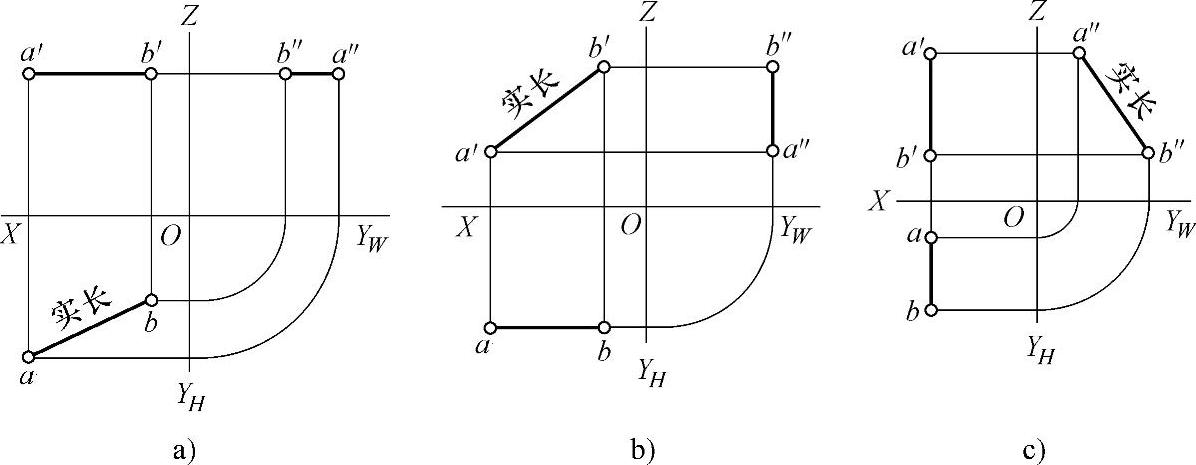
图2-26 平行线的投影

a）平行于XOY的线 b）平行于XOZ面的线 c）平行于ZOY面的线

3）一般位置直线。正投影中，与三个投影面均倾斜的线段称为一般位置直线。一般位置直线在三个投影面上的投影均不反映实长，如图2-27所示。

4）曲线。曲线可分为平面曲线和空间曲线。

①平面曲线。平面曲线的投影是否反映实长，由该曲线所在平面的位置来决定。位于平行面上的曲线，在与它平行的投影面上的投影反映实长，而另两个投影面上的投影则为平行于投影轴的直线（见图2-28a）；位于垂直面上的曲线，在其所垂直的投影面上的投影积聚成直线，而在另外两投影面上的投影仍为曲线，但不反映实长（见图2-28b）。曲线若位于一般位置平面上，则其三面投影均不反映实长（见图2-28c）。

图2-27 一般位置直线的投影

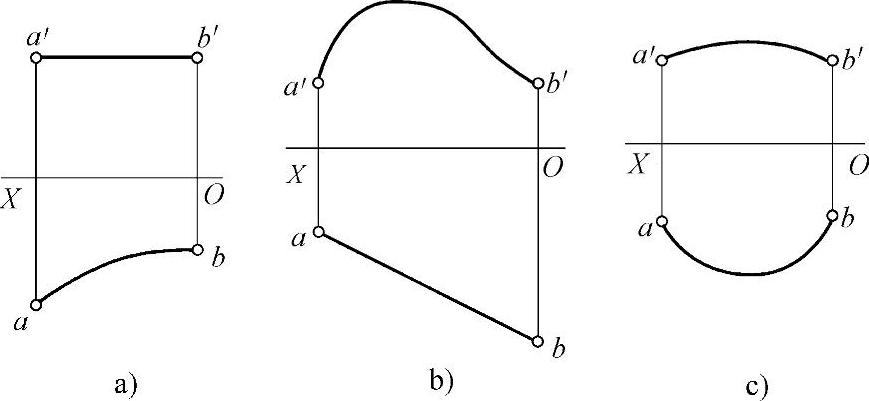
图2-28 曲线的投影

a）、b）平面曲线 c）空间曲线

②空间曲线。空间曲线又称翘曲线，这种曲线上各点不在同一平面上，它的各面投影均不反映实长。图2-28c所示为一空间曲线的投影。

注意，只有根据线段的两面或三面投影，才能对其投影是否反映实长做出正确的判断。因此，在做构件的展开时，首先需要一一对应地找出构件上各线段的投影，以确定非实长线段。

（2）求直线段实长 由前述可知，空间一般位置直线的三面投影都不反映实长。在这种情况下，就要运用投影改造的方法求出一般位置直线段的实长。

1）直角三角形法。图2-29a所示为一般位置线段AB的直观图。现在分析线段和它的投影之间的关系，以寻找求线段实长的图解方法。过点B作H面垂线，过点A作H面平行线且与垂线交于点C，成直角三角形ABC，其斜边AB是空间线段的实长。两直角边的长度可在投影图上量得：一直角边AC的长度等于线段的水平投影ab；另一直角边BC是线段两端点A、B距水平投影面的距离之差，其长度等于正面投影图中的b′c′。

由上述分析得直角三角形法求实长的投影作图方法，如图2-29b和图2-29c所示。根据实际需要，直角三角形法求实长也可以在投影图外作图（见图2-29d）。

直角三角形法求实长的作图要领如下：

①做一个直角。

②令直角的一边等于线段在某一投影面上的投影长，直角的另一边等于线段两端点相对于该投影面的距离差（此距离差可由线段的另一面投影图量取）。

③连接直角两边端点成一直角三角形，则其斜边即为线段的实长。

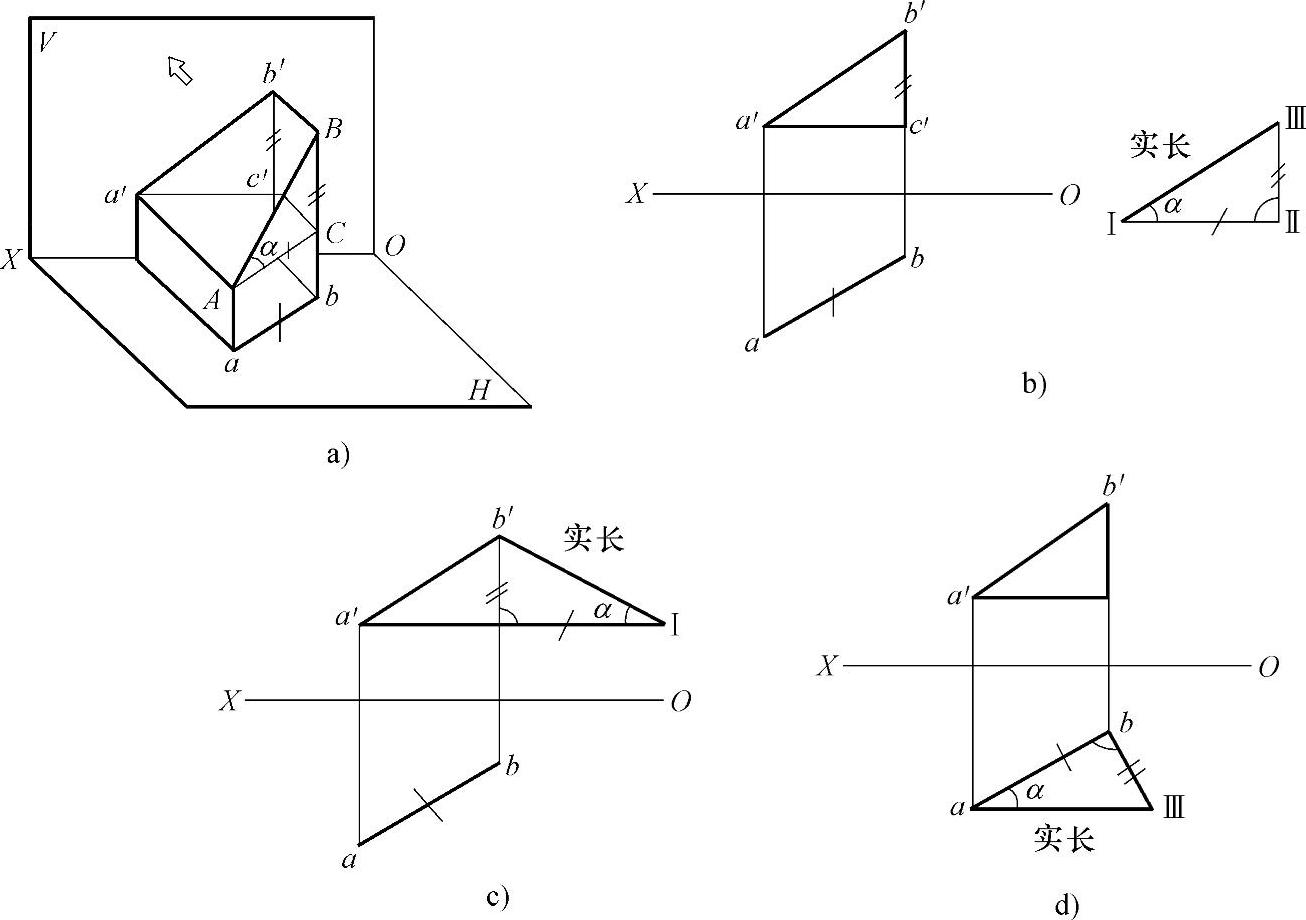
图2-29 直角三角形法求实长

a）一般位置线段AB的直观图 b）、c）直角三角形投影作图法 d）投影图外作图求实长

例12 直角三角形法求实长的应用。

图2-30所示为工厂常见的圆方过渡接头的立体图和主、俯视图。俯视图中四个全等的等腰三角形表示其平面部分，各等腰线为圆方过渡线（平面与曲面的分界线）。这些线均为一般位置直线，在视图中不反映实长。为展开需要，还需在曲面部分作出一些辅助线，如B—2、B—3（2、3点为1/4圆角的等分点），这些辅助线也是一般位置直线，投影不反映实长。

实长线求法：上述各线的实长，实际放样时多直接在主视图中作出。为使图面清晰，将求实长作图移至主视图右侧。即以各线段正面投影高度差（距离差）CD为一直角边，以各线的水平投影长f₁、f₂为另一直角边，画出两直角三角形，则三角形的斜边即为所求线段的实长。

2）旋转法。旋转法求实长，是将空间一般位置直线绕一垂直于投影面的固定旋转轴旋转成投影面平行线，则该直线在与之平行的投影面上的投影反映实长。如图2-31a所示，以AO为轴，将一般位置直线AB旋转至与正面平行的AB₁位置。此时，线段AB已由一般位置变为正平位置，其新的正面投影a′b₁′，即为AB的实长。图2-31b所示为旋转法求实长的投影作图。图2-31c所示为将AB线旋转成水平位置以求其实长的作图过程。

旋转法求实长的作图要领：(www.xing528.com)

①过线段一端点设一与投影面垂直的旋转轴。

②在与旋转轴所垂直的投影面上，将线段的投影绕该轴（投影为一个点）旋转至与投影轴平行。

③作线段旋转后与之平行的投影面上的投影，则该投影反映线段实长。

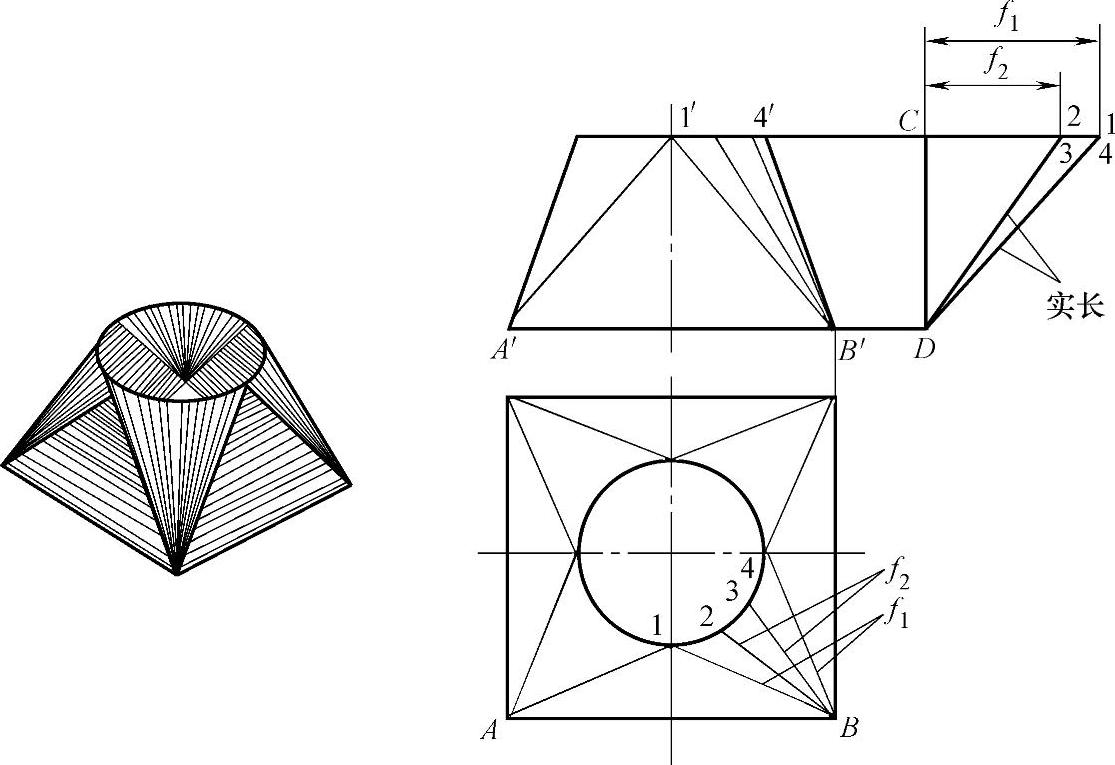
图2-30 直角三角形法求实长举例

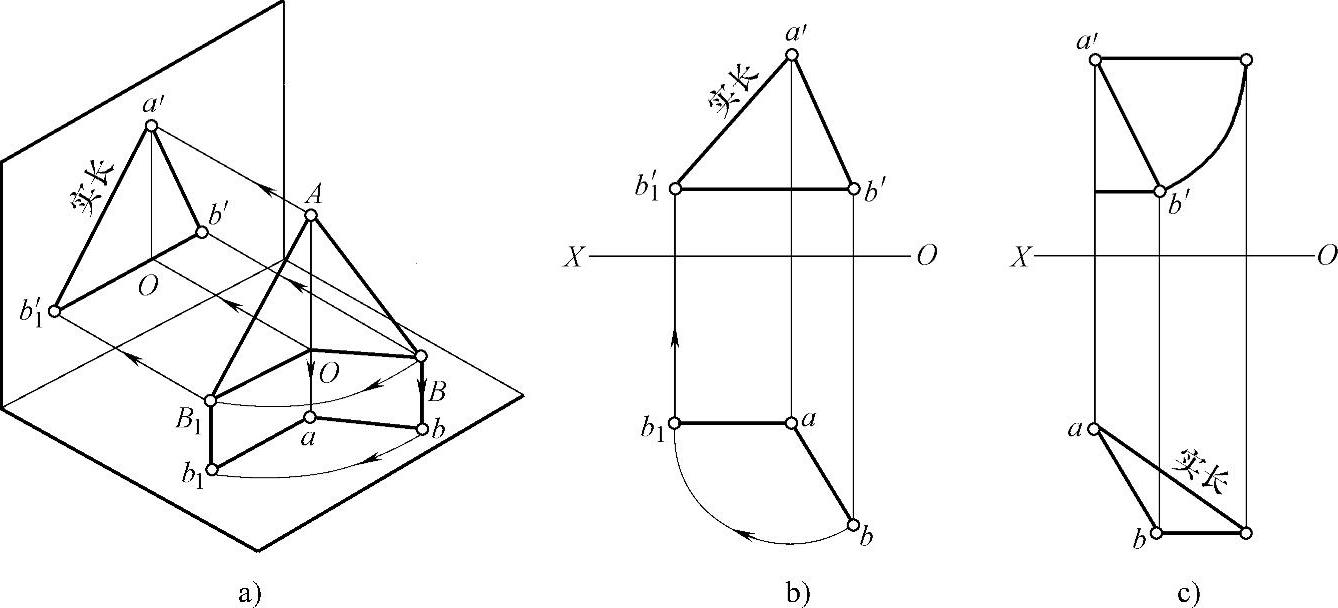
图2-31 旋转法求实长

a）空间投影 b）旋转法求实长的投影作图 c）作图过程

例13 旋转法求实长的应用。

图2-32所示为一个斜圆锥，为作出斜圆锥表面的展开图，需先求出其圆周各等分点与锥顶连线（素线）的实长。由图2-32可知，这些素线除主视图两边轮廓线（O′—1′、O′—5′）外，均不反映实长。

实长线求法：以O为圆心，O至2、3、4各点的距离为半径画同心圆弧，得到与水平中心线O—5的各交点。由各交点引上垂线交1′—5′于2′、3′、4′点，连接2′、3′、4′与O′；则O′—2′、O′—3′、O′—4′即为所求三条素线的实长。

3）换面法。如前所述，当线段与某一投影面平行时，它在该投影面上的投影反映实长。换面法求实长就是根据线段投影的这一规律，当空间线段与投影面不平行时，设法用一新的与空间线段平行的投影面，替换原来的投影面，则线段在新投影面上的投影就能反映实长，如图2-33所示。

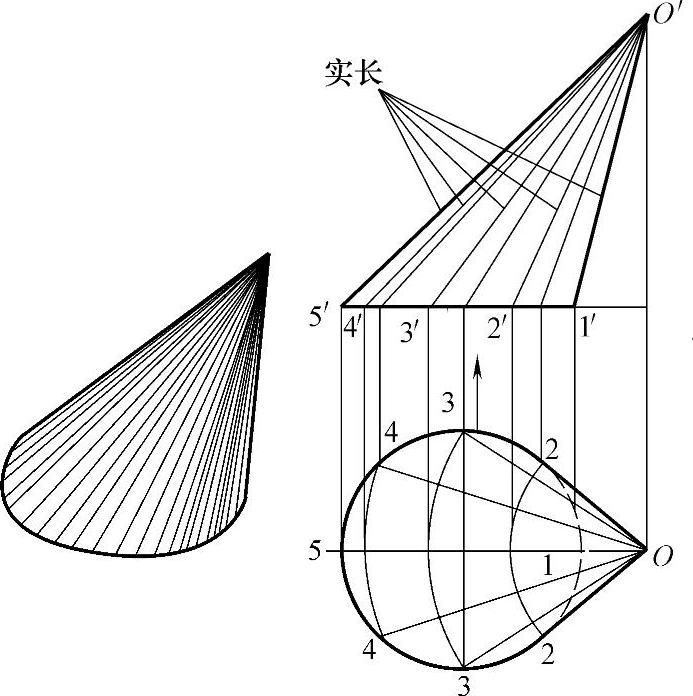
图2-32 旋转法求实长举例

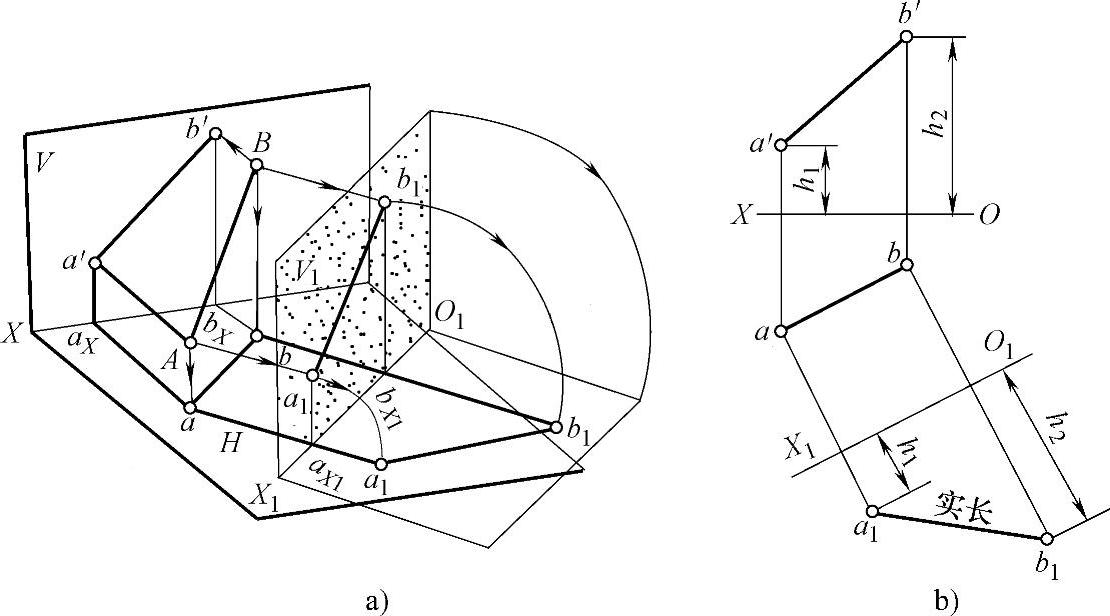
图2-33 换面法求实长

a）空间投影 b）换面法投影作图

换面法求实长的作图要领：

①新设的投影轴应与线段的一投影平行。

②新引出的投影连线要与新设的投影轴垂直。

③新投影面上点的投影至投影轴的距离，应与新投影面所替代的原投影面上点的投影至投影轴的距离相等。

在实际放样时，当构件上求实长的线段较多时，直接应用换面法求实长，会使样图上图线过多，显得零乱。这时，往往将求实长作图从投影图中移出，如图2-34所示。换面法的移出作图形式，也常称为直角梯形法。

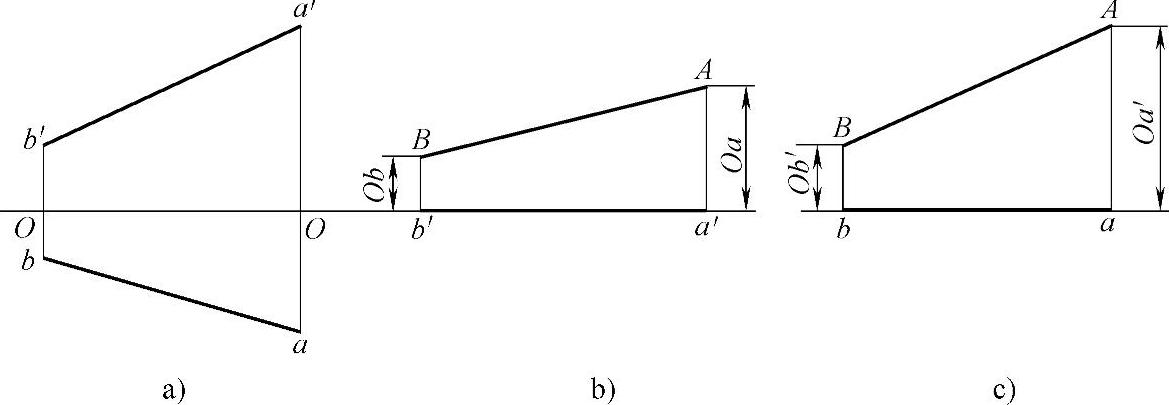
图2-34 换面法移出作图

a）投影图 b）与投影a′b′平行的换面法 c）与投影ab平行的换面法

例14 换面法求实长的应用举例。

如图2-35所示为一个顶口与底口垂直的圆方过渡接头，它表面各线的实长就是利用换面法移出作图求出的。

图2-35 换面法求实长应用举例

（3）求曲线实长 求曲线实长，通常是将曲线划分为若干段，当分段足够多时，即可把每一段都近似视为直线，然后再用上述求线段实长的方法，逐段求出其实长。图2-36所示为一个斜截圆柱，求它的斜口曲线实长就采用了换面移出作图法，按分段顺序求出每段实长，再连成光滑曲线。

当曲线为平面曲线，又垂直于投影面时，更可直接应用换面法求出其实长，而不必分段如图2-37所示。

图2-36 求柱体斜口曲线实长

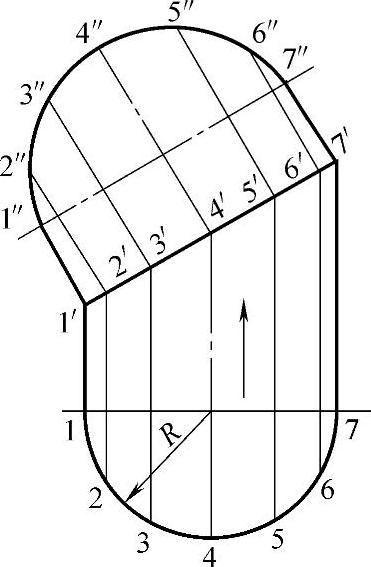
图2-37 换面法求平面曲线实长