手工编程是编程员采用数学方法，借助简单的计算工具，对编程所需的各坐标点（称为节点）进行处理和计算，手工书写数控加工程序的过程。手工编程是一种“低级语言”，当零件的形状复杂或有非圆曲线时，手工编程的方法常常非常困难，此时可使用系统提供的宏编程指令或用第三方的自动编程软件来完成零件的数控加工程序的编写工作。
随着计算机应用的深入，在刀具轨迹生成方面，基本上走过了从类似于高级语言为特色的APT时代，进入了以人机交互为主的会话式编程的CAD/CAM时代。
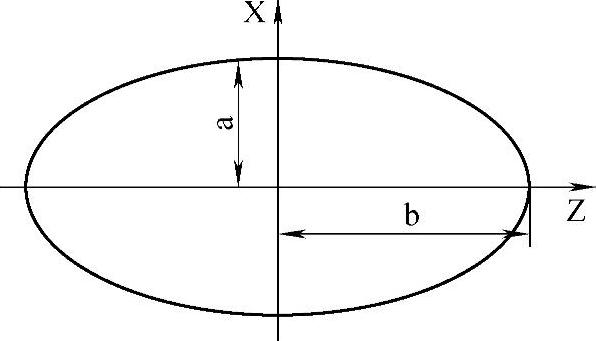
图2-17 椭圆
1.宏编程的一般方法
宏编程是类似于高级语言的一种程序，用户可以使用变量进行算术运算、逻辑运算和函数的混合运算，此外宏程序还提供了循环语句、分支语句和子程序调用语句，利于编制各种复杂的零件加工程序，减少乃至免除了手工编程时繁琐的数值计算，以及精简程序量。
图2-17所示为一椭圆，由于一般数控系统都没有提供椭圆插补指令，要想加工椭圆，所以这里要想办法用系统能够提供的方法来实现它。椭圆是非圆二次曲线，形状比较复杂，一般要在数控机床上进行加工。因为普通数控机床有直线插补功能和圆弧插补功能，所以用数控机床加工椭圆，有两种逼近方法：一是圆弧逼近法；二是直线逼近法。其中直线逼近法应用较多。
（1）基本原理 如图2-18所示，以一段椭圆弧为例说明直线逼近法。若在椭圆弧上均匀插入适当数量的点，再将这些点用直线连接起来，这一系列的直线就接近椭圆。插入的点越多，直线就越接近椭圆。但插入的点太多，就会加大数控系统的计算负担，降低加工效率，所以在实际加工中只要能够达到图纸要求（表面粗糙度）就可以了。
图2-17所示椭圆方程的形式有两种：一是标准方程形式，其方程为
；二是参数方程形式，其方程为
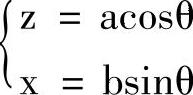0＜θ≤360°。对应椭圆方程的两种形式，就有两种椭圆宏程序的编制方法。
图2-18 直线逼近法原理
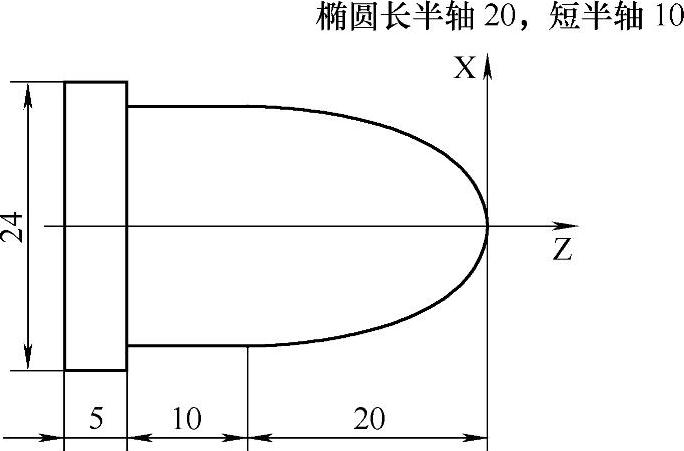
图2-19 椭圆的宏程序实例1
（2）椭圆的宏程序实例1要加工如图2-19所示的零件，方法1：按标准方程形式编写宏程序。将标准方程改写成x=±a
，本例中x取正值，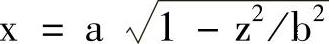
。
O0001；
M03S800F0.1；
N020T0101；
N030G00Z5；
N040X0；
#3=20；（椭圆长半轴）
#4=10；（椭圆短半轴）
#1=20；（Z轴坐标初始值）
N060#2=#4∗SQRT[1-[#1∗#1]/[#3∗#3]]；（X轴坐标）
N070G01X[2∗#2]Z[#1-20]；（直径编程，坐标平移）
N080#1=#1-0.1；（下一个点Z轴坐标）
N090IF[#1GE0]GOTO60；（终点判断）
N100Z-30；
N110X24；
N120Z-35；
N130G0X100；
Z200；
M30；
%
方法2：按参数方程形式编写宏程序。
O0002；
M03S800F0.1；
N020T0101；
N030G00Z5；
N040X0；
#4=20；（椭圆长半轴）
#5=10；（椭圆短半轴）
#1=0；（参数角度初始值）
N060#2=#4∗COS[#1]；（Z轴坐标）
#3=#5∗SIN[#1]；（X轴坐标）(www.xing528.com)
N070G01X[2∗#3]Z[#2-20]；（直径编程，坐标平移）
N080#1=#1+1；（下一个点参数角度）
N090IF[#1LE90]GOTO60；（终点判断）
N100Z-30；
N110X24；
N120Z-35；
N130G0X100；
Z200；
M30；
%
（3）椭圆的宏程序实例2实例2如图2-20所示，本例中x取负值，x=-a
。其标准方程方法的参考程序如下：
O0003；
M03S800F0.1；
N020T0101；
N030G00Z5；
N040X25；
#3=20；（椭圆长半轴）
#4=10；（椭圆短半轴）
#1=38.73/2；（Z轴坐标初始值）
N060#2=-#4∗SQRT[1-[#1∗#1]/[#3∗#3]]；（X轴坐标）
N070G01X[2∗[#2+15]]Z[#1-24.36]；（直径编程，坐标平移）
N080#1=#1-0.1；（下一个点Z轴坐标）
N090IF[#1GE-38.73/2]GOTO60；（终点判断）
N100Z-48.73；
N110X26；
N130G0X100；
Z200；
M30；
%
图2-20 椭圆的宏程序实例2
图2-21 椭圆坐标平移
值得注意的是，当数控车床加工的零件的椭圆中心不在回转轴上时，椭圆的方程需要经过坐标平移，如图2-21所示。
坐标平移之后，在新的坐标系下的坐标为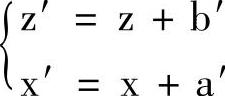
。
2.自动编程的工作过程
一个集成化的CAD/CAM数控编程系统，一般由几何造型、刀具轨迹生成、刀具轨迹编辑、刀具轨迹验证、后置处理、图形显示及用户界面等部分组成。在数控车床的自动编程系统中，其基本的工作过程包括：
（1）分析加工零件 当拿到待加工零件的零件图样或工艺图样（特别是复杂曲面零件和模具图样）时，首先应当对零件图样进行仔细的分析，内容包括：分析待加工表面、确定加工方法、确定编程原点及编程坐标系等。
（2）对待加工表面及其约束面进行几何造型 这是数控加工编程的第一步。对于现代CAD/CAM集成数控编程系统来说，大多数软件已采用三维实体造型的方法来描述零件的几何特征信息（孔、槽、各种成形面等）。
（3）确定工艺步骤并选择刀具 一般来说，可根据加工方法和加工表面及其约束面的几何形态选择合适的刀具类型及刀具尺寸。当根据经验和直觉选择刀具时，为保证所选择的刀具是合适的，在刀具轨迹生成之后，需要进行一定的刀具轨迹验证。
（4）刀具轨迹生成及刀具轨迹编辑 对于CAD/CAM集成数控编程系统来说，一般可在所定义加工表面及其约束面（或加工单元）上确定其法向矢量方向，并选择一种走刀方式，根据所选择的刀具（或定义的刀具）和加工参数，系统将自动生成所需的刀具轨迹。刀具轨迹生成后，如果系统具备刀具轨迹显示及交互编辑功能，则可以将刀具轨迹显示出来，如果有不太合适的地方，可以在人工交互方式下对刀具轨迹进行适当的编辑与修改。
（5）刀具轨迹验证 如果系统具有刀具轨迹验证功能，对可能过切、干涉与碰撞的刀位点，采用系统提供的刀具轨迹验证手段进行检验。
（6）后置处理 根据所选用的数控系统，调用其机床数据文件，运行数控编程系统提供的后置处理程序，将刀位原文件转换成数控加工程序。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
